Difference between revisions of "Signal Representation/The Fourier Transform Theorems"
| Line 20: | Line 20: | ||
| − | + | This relation can be used for simplification by omitting the constant $k$ (which can be a gain-, a damping- or a unit-factor) and adding it to the result later. | |
| − | + | The above sentence follows directly from the definition of [[Signal_Representation/Fourier_Transform_and_Its_Inverse#Das_erste_Fourierintegral|the first Fourier integral]], as well as from the addition theorem, which formulates the foundation of the '''superposition principle''' . | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Addition Theorem:}$ If a time function can be written as a sum of single functions, the resulting spectral function is the sum of the resulting single spectra: |
:$$x( t ) = x_1 ( t ) + x_2 ( t )\quad\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad X( f ) = X_1 (f) + X_2 ( f ).$$ }} | :$$x( t ) = x_1 ( t ) + x_2 ( t )\quad\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad X( f ) = X_1 (f) + X_2 ( f ).$$ }} | ||
| − | [[File:P_ID2722__Sig_T_3_3_S1.png|right|frame| | + | [[File:P_ID2722__Sig_T_3_3_S1.png|right|frame|Rectangular pulse, triangular pulse and their combination]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ The following Fourier correspondences are known: |
| − | * | + | *The rectangular pulse: |
:$$x_1 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_1 ( f )=T \cdot {\rm si}(\pi f T),$$ | :$$x_1 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_1 ( f )=T \cdot {\rm si}(\pi f T),$$ | ||
| − | * | + | *The triangle pulse: |
:$$ x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_2 ( f )=T /2\cdot {\rm si}(\pi f T/2).$$ | :$$ x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_2 ( f )=T /2\cdot {\rm si}(\pi f T/2).$$ | ||
| − | + | These two impulse signals are sketched as red and blue curve respectively. | |
| − | + | Then the green drawn (weighted) sum signal is valid: | |
:$$x(t) = {1}/{3} \cdot x_1 ( t ) + {2}/{3} \cdot x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f) = {1}/{3} \cdot X_1 ( f ) + {2}/{3} \cdot X_2 ( f ).$$}} | :$$x(t) = {1}/{3} \cdot x_1 ( t ) + {2}/{3} \cdot x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f) = {1}/{3} \cdot X_1 ( f ) + {2}/{3} \cdot X_2 ( f ).$$}} | ||
| − | '' | + | ''Notes:'' All theorems presented in this chapter can be found at the german learning video [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|Fourier Transform Laws]] with illustrated examples. |
| − | == | + | ==Mapping Theorem== |
<br> | <br> | ||
| − | + | With the [[Signal_Representation/Fourier_Series#Komplexe_Fourierreihe|Complex Fourier Series]] for describing periodic signals, we have found out that that an even function always leads to real Fourier coefficients and an odd function exclusively to imaginary Fourier coefficients. The Fourier transform shows similar properties. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Mapping Theorem:}$ If a real time function consists additively of an even and an uneven part, |
:$$x( t ) = x_{\rm g} ( t ) + x_{\rm u} ( t ),$$ | :$$x( t ) = x_{\rm g} ( t ) + x_{\rm u} ( t ),$$ | ||
| − | + | then the following applies for its spectral function: | |
| − | + | :$$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f), \hspace{0.5cm}\text{with}$$ | |
| − | :$$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f), \hspace{0.5cm}\text{ | ||
::$$ x_{\rm g} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X_{\rm R}(f),$$ | ::$$ x_{\rm g} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X_{\rm R}(f),$$ | ||
::$$x_{\rm u} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} {\rm j} \cdot X_{\rm I} (f).$$ | ::$$x_{\rm u} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} {\rm j} \cdot X_{\rm I} (f).$$ | ||
| − | + | The real part $X_{\rm R}(f)$ of the spectrum is then also even, while $X_{\rm I}(f)$ describes an odd function of the frequency.}} | |
| − | + | The assignment theorem can be easily proved by considering the theorem of [https://en.wikipedia.org/wiki/Leonhard_Euler Leonhard Euler] ⇒ ${\rm e}^{ - {\rm j}\omega _0 t} = \cos ( {\omega _0 t} ) - {\rm j}\cdot \sin ( {\omega _0 t} )$ . The even and odd part of a function $x(t)$ can be calculated with the following equations: | |
| + | |||
:$$x_{\rm g} (t) = {1}/{2}\big[ {x(t) + x(-t)} \big],$$ | :$$x_{\rm g} (t) = {1}/{2}\big[ {x(t) + x(-t)} \big],$$ | ||
:$$x_{\rm u} (t) = {1}/{2}\big[ {x(t) - x(-t)} \big].$$ | :$$x_{\rm u} (t) = {1}/{2}\big[ {x(t) - x(-t)} \big].$$ | ||
| − | [[File:P_ID472__Sig_T_3_3_S2.png|right|frame| | + | [[File:P_ID472__Sig_T_3_3_S2.png|right|frame|Spectrum of a Jumping Function]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | We consider the ''Jump Function'' | |
:$$x(t) = \gamma (t) = \bigg\{ \begin{array}{l} 0\quad \quad {\rm f\ddot{u} r}\;t < 0 \\ 1\quad \quad{\rm f\ddot{u} r}\; t > 0 \\ \end{array} ,$$ | :$$x(t) = \gamma (t) = \bigg\{ \begin{array}{l} 0\quad \quad {\rm f\ddot{u} r}\;t < 0 \\ 1\quad \quad{\rm f\ddot{u} r}\; t > 0 \\ \end{array} ,$$ | ||
| − | + | which can be split as follows: | |
:$$\gamma (t) = {1}/{2} +{1}/{2} \cdot {\rm sign}(t).$$ | :$$\gamma (t) = {1}/{2} +{1}/{2} \cdot {\rm sign}(t).$$ | ||
| − | + | The ''Signum function'' was used here: | |
:$${\rm sign} (t) = \bigg\{ \begin{array}{l} -1\quad \quad {\rm f\ddot{u} r}\;t < 0, \\ +1\quad \quad{\rm f\ddot{u} r}\; t > 0. \\ \end{array} $$ | :$${\rm sign} (t) = \bigg\{ \begin{array}{l} -1\quad \quad {\rm f\ddot{u} r}\;t < 0, \\ +1\quad \quad{\rm f\ddot{u} r}\; t > 0. \\ \end{array} $$ | ||
| − | + | Therefore the following applies: | |
| − | * | + | *The even (blue) signal portion $x_{\rm g} (t) = {1}/{2}$ is a constant with the real spectral function $X_{\rm R}(f) = {1}/{2} \cdot \delta(f)$. |
| − | * | + | *The spectrum ${\rm j} \cdot X_{\rm I}(f)$ the odd (green) signum function $x_{\rm u} (t)$ was already calculated in the earlier [[Signal_Representation/Fourier_Transform_and_Its_Inverse#Fouriertransformation|$\text{Example 3}$]] n the page „Fouriertransformation”. |
| − | * | + | *This results in the jump function  for the resulting spectrum of the red sketched jump function; |
| − | |||
:$$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f)= {1}/{2} \cdot \delta (f) - {\rm j}\cdot \frac{1}{2\pi f}.$$}} | :$$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f)= {1}/{2} \cdot \delta (f) - {\rm j}\cdot \frac{1}{2\pi f}.$$}} | ||
| − | == | + | ==Similarity Theorem== |
<br> | <br> | ||
| − | + | The similarity theorem shows the relation between the spectral functions of two time signals of the same shape, stretched or compressed. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Simity Theoremlari:}$ If $X(f)$ the Fourier transform of $x(t)$, then with the real constant $k$ the following relation appliesg: |
:$$x( {k \cdot t} )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} \frac{1}{\left \vert k \right \vert} \cdot X( {f}/{k} ).$$}} | :$$x( {k \cdot t} )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} \frac{1}{\left \vert k \right \vert} \cdot X( {f}/{k} ).$$}} | ||
| Line 106: | Line 105: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Proof:}$ For positive $k$ follows from the Fourier integral with the substitution $\tau = k \cdot t$: |
:$$\int_{ - \infty }^{ + \infty } {x( {k \cdot t})} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}ft} \hspace{0.1cm}{\rm d}t = \frac{1}{k} \cdot \int_{ - \infty }^{ + \infty } {x( \tau )} \cdot {\rm e}^{ - {\rm j}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f/k \hspace{0.05cm}\cdot \hspace{0.05cm}\tau } \hspace{0.1cm}{\rm d} \tau = \frac{1}{k}\cdot X( {{f}/{k}}).$$ | :$$\int_{ - \infty }^{ + \infty } {x( {k \cdot t})} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}ft} \hspace{0.1cm}{\rm d}t = \frac{1}{k} \cdot \int_{ - \infty }^{ + \infty } {x( \tau )} \cdot {\rm e}^{ - {\rm j}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f/k \hspace{0.05cm}\cdot \hspace{0.05cm}\tau } \hspace{0.1cm}{\rm d} \tau = \frac{1}{k}\cdot X( {{f}/{k}}).$$ | ||
| − | * | + | *For negative $k$ the integration limits would be mixed up and you get $-1/k \cdot X(f/k)$. |
| − | * | + | *Since in the equation $\vert k \vert$ is used, the result is valid for both signs. |
<div align="right">q.e.d.</div>}} | <div align="right">q.e.d.</div>}} | ||
| − | + | The effects of the similarity theorem can be illustrated with a tape for example. If such a tape is played with double speed, this corresponds to a compression of the time signal $(k = 2)$. Thus the frequencies appear twice as high. | |
| − | [[File:P_ID473__Sig_T_3_3_S3_neu.png|right|frame| | + | [[File:P_ID473__Sig_T_3_3_S3_neu.png|right|frame|Two Rectangles of different width]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
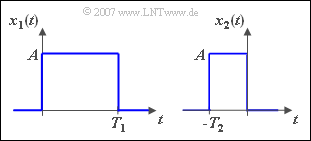
| − | $\text{ | + | $\text{Example 3:}$ |
Wir betrachten zwei Rechtecke gleicher Höhe, wobei $T_2 = T_1/2$ gilt. | Wir betrachten zwei Rechtecke gleicher Höhe, wobei $T_2 = T_1/2$ gilt. | ||
| − | * | + | *The spectral function of $x_1(t)$ results after the [[Signal_Representation/Fourier_Transform_and_Its_Inverse#Das_erste_Fourierintegral|first Fourier Integral]] to |
:$$X_1 (f) = A \cdot \frac{ {1 - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } } }{ { {\rm j}2\pi f} } .$$ | :$$X_1 (f) = A \cdot \frac{ {1 - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } } }{ { {\rm j}2\pi f} } .$$ | ||
| − | * | + | *For this can also be written: |
| − | + | ||
:$$X_1 (f) = A \cdot T_1 \cdot \frac{{{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } }}{{{\rm j}2\pi fT_1 }} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } = A \cdot T_1 \cdot {\rm si}( {\pi f T_1 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 }.$$ | :$$X_1 (f) = A \cdot T_1 \cdot \frac{{{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } }}{{{\rm j}2\pi fT_1 }} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } = A \cdot T_1 \cdot {\rm si}( {\pi f T_1 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 }.$$ | ||
| − | * | + | *For the spectral function of $x_2(t)$ follows from the similarity theorem with $k = -2$: |
:$$X_2 (f) = \frac{1}{2} \cdot X_1 ( { - {f}/{2}} ) = \frac{A \cdot T_1 }{2} \cdot {\rm si}( { - \pi f {T_1 }/{2} } ) \cdot {\rm e}^{ {\rm j}\pi fT_1 /2} .$$ | :$$X_2 (f) = \frac{1}{2} \cdot X_1 ( { - {f}/{2}} ) = \frac{A \cdot T_1 }{2} \cdot {\rm si}( { - \pi f {T_1 }/{2} } ) \cdot {\rm e}^{ {\rm j}\pi fT_1 /2} .$$ | ||
| − | * | + | *The $\text{si}$–function is even: $\text{si}(-x) = \text{si}(x)$. Therefore you can omit the sign in the argument of the $\text{si}$–function. |
| − | * | + | *With $T_2 = T_1/2$ one gets: |
:$$X_2 (f) = A \cdot T_2 \cdot {\rm si}( {\pi fT_2 } ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_2 } .$$}} | :$$X_2 (f) = A \cdot T_2 \cdot {\rm si}( {\pi fT_2 } ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_2 } .$$}} | ||
| − | == | + | ==Reciprocity Theorem of Time duration and Bandwidth== |
<br> | <br> | ||
| − | + | This law follows directly from the Signal_Representation/Fourier_Transform_Laws#.C3.84hnlichkeitssatz|Similarity Theorem]]: The wider an impulse is in its extension, the narrower and higher is the corresponding spectrum and vice versa. | |
| − | + | To be able to make quantitative statements, we define two parameters for energy-limited signals ⇒ Impulse. Both quantities are shown in the diagram for the $\text{Example 4}$ for a Gaussian pulse and its likewise Gaussian spectrum. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The '''equivalent pulse duration''' is derived from the time course. It is equal to the width of an area equal rectangle with the same height as $x(t)$: | |
:$$\Delta t = \frac{1}{{x( {t = 0} )}} \cdot \int_{ - \infty }^{ + \infty } {x( t)} \hspace{0.1cm}{\rm d}t.$$}} | :$$\Delta t = \frac{1}{{x( {t = 0} )}} \cdot \int_{ - \infty }^{ + \infty } {x( t)} \hspace{0.1cm}{\rm d}t.$$}} | ||
| Line 157: | Line 156: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The '''equivalent bandwidth''' denotes the impulse in the frequency domain. It gives the width of the area equal rectangle with the same height as the spectrum $X(f)$: | |
:$$\Delta f = \frac{1}{{X( {f = 0} )}}\cdot \int_{ - \infty }^{ + \infty } {X( f )} \hspace{0.1cm} {\rm d}f.$$}} | :$$\Delta f = \frac{1}{{X( {f = 0} )}}\cdot \int_{ - \infty }^{ + \infty } {X( f )} \hspace{0.1cm} {\rm d}f.$$}} | ||
| Line 163: | Line 162: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Reciprocity Theorem:}$ Das Produkt aus äquivalenter Impulsdauer und äquivalenter Bandbreite ist stets gleich $1$: |
:$$\Delta t \cdot \Delta f = 1$$}} | :$$\Delta t \cdot \Delta f = 1$$}} | ||
| Line 169: | Line 168: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Proof:}$ |
| − | + | Based on the two Fourier integrals, for $f = 0$ or. $t = 0$: | |
:$$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,} \hspace{0.5cm}x( {t = 0} ) = \int_{ - \infty }^{ + \infty } {X(f)\hspace{0.1cm}{\rm d}f.}$$ | :$$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,} \hspace{0.5cm}x( {t = 0} ) = \int_{ - \infty }^{ + \infty } {X(f)\hspace{0.1cm}{\rm d}f.}$$ | ||
| − | + | If you take this result into account in the above definitions, you get | |
:$$\Delta t = \frac{{X( {f = 0} )}}{{x( {t = 0} )}}, \hspace{0.5cm}\Delta f = \frac{{x( {t = 0} )}}{{X( {f = 0} )}}.$$ | :$$\Delta t = \frac{{X( {f = 0} )}}{{x( {t = 0} )}}, \hspace{0.5cm}\Delta f = \frac{{x( {t = 0} )}}{{X( {f = 0} )}}.$$ | ||
| − | + | From this $\Delta t \cdot \Delta f = 1$follows directly. <div align="right">q.e.d.</div>}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | Note that $\Delta f$ is defined over the actual spectrum $X(f)$ and not over $|X(f)|$ . | ||
| + | *For real functions the integration over the even function part is sufficient, since the integral over the odd part is always zero due to the [[Signal_Representation/Fourier_Transform_Laws#Zuordnungssatz|Mapping Theorem]] . | ||
| + | *For odd time functions and thus purely imaginary spectra, the two definitions of $\Delta t$ and. $\Delta f$ fail. | ||
[[File:Sig_T_3_4_S4_version2.png|right|frame|Gauß–Beispiel zum Reziprozitätsgesetz]] | [[File:Sig_T_3_4_S4_version2.png|right|frame|Gauß–Beispiel zum Reziprozitätsgesetz]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ |
Die Grafik verdeutlicht die äquivalente Impulsdauer $\Delta t$ und die äquivalente Bandbreite $\Delta f$ beispielhaft für den Gaußimpuls. Weiter gilt: | Die Grafik verdeutlicht die äquivalente Impulsdauer $\Delta t$ und die äquivalente Bandbreite $\Delta f$ beispielhaft für den Gaußimpuls. Weiter gilt: | ||
*Verbreitert man den Gaußimpuls um den Faktor $3$, so wird die äquivalente Bandbreite um den gleichen Faktor kleiner. | *Verbreitert man den Gaußimpuls um den Faktor $3$, so wird die äquivalente Bandbreite um den gleichen Faktor kleiner. | ||
Revision as of 16:55, 16 November 2020
Contents
Multiplication With a Factor - Addition Theorem
In this section the Fourier Transform Theorems are assembled. These can be used to e.g. derive from already known transformations
- $$x( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f ),\quad x_1 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 ( f ),\quad x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_2 ( f )$$
new functional relationships. Here we restrict ourselves to real time functions.
$\text{Theorem:}$ A constant factor $k$ affects the time and spectral function in the same way:
- $$k \cdot x(t)\ \;\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ k \cdot X(f).$$
This relation can be used for simplification by omitting the constant $k$ (which can be a gain-, a damping- or a unit-factor) and adding it to the result later.
The above sentence follows directly from the definition of the first Fourier integral, as well as from the addition theorem, which formulates the foundation of the superposition principle .
$\text{Addition Theorem:}$ If a time function can be written as a sum of single functions, the resulting spectral function is the sum of the resulting single spectra:
- $$x( t ) = x_1 ( t ) + x_2 ( t )\quad\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad X( f ) = X_1 (f) + X_2 ( f ).$$
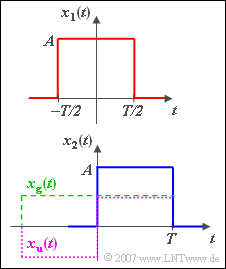
$\text{Example 1:}$ The following Fourier correspondences are known:
- The rectangular pulse:
- $$x_1 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_1 ( f )=T \cdot {\rm si}(\pi f T),$$
- The triangle pulse:
- $$ x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_2 ( f )=T /2\cdot {\rm si}(\pi f T/2).$$
These two impulse signals are sketched as red and blue curve respectively.
Then the green drawn (weighted) sum signal is valid:
- $$x(t) = {1}/{3} \cdot x_1 ( t ) + {2}/{3} \cdot x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f) = {1}/{3} \cdot X_1 ( f ) + {2}/{3} \cdot X_2 ( f ).$$
Notes: All theorems presented in this chapter can be found at the german learning video Fourier Transform Laws with illustrated examples.
Mapping Theorem
With the Complex Fourier Series for describing periodic signals, we have found out that that an even function always leads to real Fourier coefficients and an odd function exclusively to imaginary Fourier coefficients. The Fourier transform shows similar properties.
$\text{Mapping Theorem:}$ If a real time function consists additively of an even and an uneven part,
- $$x( t ) = x_{\rm g} ( t ) + x_{\rm u} ( t ),$$
then the following applies for its spectral function:
- $$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f), \hspace{0.5cm}\text{with}$$
- $$ x_{\rm g} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X_{\rm R}(f),$$
- $$x_{\rm u} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} {\rm j} \cdot X_{\rm I} (f).$$
The real part $X_{\rm R}(f)$ of the spectrum is then also even, while $X_{\rm I}(f)$ describes an odd function of the frequency.
The assignment theorem can be easily proved by considering the theorem of Leonhard Euler ⇒ ${\rm e}^{ - {\rm j}\omega _0 t} = \cos ( {\omega _0 t} ) - {\rm j}\cdot \sin ( {\omega _0 t} )$ . The even and odd part of a function $x(t)$ can be calculated with the following equations:
- $$x_{\rm g} (t) = {1}/{2}\big[ {x(t) + x(-t)} \big],$$
- $$x_{\rm u} (t) = {1}/{2}\big[ {x(t) - x(-t)} \big].$$
$\text{Example 2:}$ We consider the Jump Function
- $$x(t) = \gamma (t) = \bigg\{ \begin{array}{l} 0\quad \quad {\rm f\ddot{u} r}\;t < 0 \\ 1\quad \quad{\rm f\ddot{u} r}\; t > 0 \\ \end{array} ,$$
which can be split as follows:
- $$\gamma (t) = {1}/{2} +{1}/{2} \cdot {\rm sign}(t).$$
The Signum function was used here:
- $${\rm sign} (t) = \bigg\{ \begin{array}{l} -1\quad \quad {\rm f\ddot{u} r}\;t < 0, \\ +1\quad \quad{\rm f\ddot{u} r}\; t > 0. \\ \end{array} $$
Therefore the following applies:
- The even (blue) signal portion $x_{\rm g} (t) = {1}/{2}$ is a constant with the real spectral function $X_{\rm R}(f) = {1}/{2} \cdot \delta(f)$.
- The spectrum ${\rm j} \cdot X_{\rm I}(f)$ the odd (green) signum function $x_{\rm u} (t)$ was already calculated in the earlier $\text{Example 3}$ n the page „Fouriertransformation”.
- This results in the jump function  for the resulting spectrum of the red sketched jump function;
- $$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f)= {1}/{2} \cdot \delta (f) - {\rm j}\cdot \frac{1}{2\pi f}.$$
Similarity Theorem
The similarity theorem shows the relation between the spectral functions of two time signals of the same shape, stretched or compressed.
$\text{Simity Theoremlari:}$ If $X(f)$ the Fourier transform of $x(t)$, then with the real constant $k$ the following relation appliesg:
- $$x( {k \cdot t} )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} \frac{1}{\left \vert k \right \vert} \cdot X( {f}/{k} ).$$
$\text{Proof:}$ For positive $k$ follows from the Fourier integral with the substitution $\tau = k \cdot t$:
- $$\int_{ - \infty }^{ + \infty } {x( {k \cdot t})} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}ft} \hspace{0.1cm}{\rm d}t = \frac{1}{k} \cdot \int_{ - \infty }^{ + \infty } {x( \tau )} \cdot {\rm e}^{ - {\rm j}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f/k \hspace{0.05cm}\cdot \hspace{0.05cm}\tau } \hspace{0.1cm}{\rm d} \tau = \frac{1}{k}\cdot X( {{f}/{k}}).$$
- For negative $k$ the integration limits would be mixed up and you get $-1/k \cdot X(f/k)$.
- Since in the equation $\vert k \vert$ is used, the result is valid for both signs.
The effects of the similarity theorem can be illustrated with a tape for example. If such a tape is played with double speed, this corresponds to a compression of the time signal $(k = 2)$. Thus the frequencies appear twice as high.
$\text{Example 3:}$ Wir betrachten zwei Rechtecke gleicher Höhe, wobei $T_2 = T_1/2$ gilt.
- The spectral function of $x_1(t)$ results after the first Fourier Integral to
- $$X_1 (f) = A \cdot \frac{ {1 - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } } }{ { {\rm j}2\pi f} } .$$
- For this can also be written:
- $$X_1 (f) = A \cdot T_1 \cdot \frac{{{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } }}{{{\rm j}2\pi fT_1 }} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } = A \cdot T_1 \cdot {\rm si}( {\pi f T_1 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 }.$$
- For the spectral function of $x_2(t)$ follows from the similarity theorem with $k = -2$:
- $$X_2 (f) = \frac{1}{2} \cdot X_1 ( { - {f}/{2}} ) = \frac{A \cdot T_1 }{2} \cdot {\rm si}( { - \pi f {T_1 }/{2} } ) \cdot {\rm e}^{ {\rm j}\pi fT_1 /2} .$$
- The $\text{si}$–function is even: $\text{si}(-x) = \text{si}(x)$. Therefore you can omit the sign in the argument of the $\text{si}$–function.
- With $T_2 = T_1/2$ one gets:
- $$X_2 (f) = A \cdot T_2 \cdot {\rm si}( {\pi fT_2 } ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_2 } .$$
Reciprocity Theorem of Time duration and Bandwidth
This law follows directly from the Signal_Representation/Fourier_Transform_Laws#.C3.84hnlichkeitssatz|Similarity Theorem]]: The wider an impulse is in its extension, the narrower and higher is the corresponding spectrum and vice versa.
To be able to make quantitative statements, we define two parameters for energy-limited signals ⇒ Impulse. Both quantities are shown in the diagram for the $\text{Example 4}$ for a Gaussian pulse and its likewise Gaussian spectrum.
$\text{Definition:}$ The equivalent pulse duration is derived from the time course. It is equal to the width of an area equal rectangle with the same height as $x(t)$:
- $$\Delta t = \frac{1}{{x( {t = 0} )}} \cdot \int_{ - \infty }^{ + \infty } {x( t)} \hspace{0.1cm}{\rm d}t.$$
$\text{Definition:}$ The equivalent bandwidth denotes the impulse in the frequency domain. It gives the width of the area equal rectangle with the same height as the spectrum $X(f)$:
- $$\Delta f = \frac{1}{{X( {f = 0} )}}\cdot \int_{ - \infty }^{ + \infty } {X( f )} \hspace{0.1cm} {\rm d}f.$$
$\text{Reciprocity Theorem:}$ Das Produkt aus äquivalenter Impulsdauer und äquivalenter Bandbreite ist stets gleich $1$:
- $$\Delta t \cdot \Delta f = 1$$
$\text{Proof:}$ Based on the two Fourier integrals, for $f = 0$ or. $t = 0$:
- $$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,} \hspace{0.5cm}x( {t = 0} ) = \int_{ - \infty }^{ + \infty } {X(f)\hspace{0.1cm}{\rm d}f.}$$
If you take this result into account in the above definitions, you get
- $$\Delta t = \frac{{X( {f = 0} )}}{{x( {t = 0} )}}, \hspace{0.5cm}\Delta f = \frac{{x( {t = 0} )}}{{X( {f = 0} )}}.$$
Note that $\Delta f$ is defined over the actual spectrum $X(f)$ and not over $|X(f)|$ .
- For real functions the integration over the even function part is sufficient, since the integral over the odd part is always zero due to the Mapping Theorem .
- For odd time functions and thus purely imaginary spectra, the two definitions of $\Delta t$ and. $\Delta f$ fail.
$\text{Example 4:}$ Die Grafik verdeutlicht die äquivalente Impulsdauer $\Delta t$ und die äquivalente Bandbreite $\Delta f$ beispielhaft für den Gaußimpuls. Weiter gilt:
- Verbreitert man den Gaußimpuls um den Faktor $3$, so wird die äquivalente Bandbreite um den gleichen Faktor kleiner.
- Wenn hierbei die Impulsamplitude $x(t = 0)$ nicht verändert wird, bleibt auch die Integralfläche über $X(f)$ konstant.
- Das heißt, dass $X(f=0)$ gleichzeitig um den Faktor $3$ größer wird.
Vertauschungssatz
Diese Gesetzmäßigkeit ist besonders nützlich, um neue Fourierkorrespondenzen zu erhalten.
$\text{Vertauschungssatz:}$ Ist $X(f)$ die Fouriertransformierte von $x(t)$, dann gilt auch:
- $$X^{\star}(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}x^{\star}( f ).$$
Beschränken wir uns auf reelle Zeitfunktionen, so können die Zeichen für „konjugiert komplex” auf beiden Seiten der Fourierkorrespondenz weggelassen werden.
$\text{Beweis:}$ Das erste Fourierintegral lautet nach sukzessiver Umbenennung $t \to u$ bzw. $f \to t$:
- $$X( f ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}u} \hspace{0.1cm}{\rm d}u, \hspace{1cm} X(t ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$$
- Ändert man das Vorzeichen in den Exponenten, so muss man $X(t)$ durch $X^*(t)$ und $x(u)$ durch $x^*(u)$ ersetzen:
- $$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( u )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi\hspace{0.05cm}\cdot \hspace{0.05cm} t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$$
- Mit der weiteren Umbennung $u \to f$ kommt man zum zweiten Fourierintegral:
- $$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.\hspace{7.9cm}$$
$\text{Beispiel 5:}$ Das Spektrum $X(f) = \delta(f)$ des Gleichsignals $x(t) = 1$ wird als bekannt vorausgesetzt.
Nach dem Vertauschungssatz lautet deshalb die Spektralfunktion des Diracimpulses $x(t) = \delta(t)$:
- $$ x(t) = \delta(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)= 1.$$
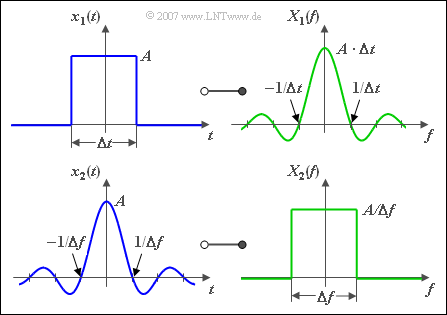
Die Grafik zeigt eine weitere Anwendung des Vertauschungssatzes, nämlich die Funktionalzusammenhänge zwischen
- einem Signal $x_1(t)$ mit rechteckförmiger Zeitfunktion, und
- einem Signal $x_2(t)$ mit rechteckförmiger Spektralfunktion.
Verschiebungssatz
Wir betrachten nun eine Verschiebung der Zeitfunktion – zum Beispiel verursacht durch eine Laufzeit – oder eine Frequenzverschiebung, wie sie beispielsweise bei der (analogen) Zweiseitenband–Amplitudenmodulation auftritt.
$\text{Verschiebungssatz:}$ Ist $X(f)$ die Fouriertransformierte (Spektralfunktion) der Zeitfunktion $x(t)$, so gelten auch folgende Zusammenhänge:
$$\mathbf{(1)}\hspace{0.5cm}x( {t - t_0 } )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( f ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 },$$
$$\mathbf{(2)}\hspace{0.5cm}x( t ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( {f - f_0 } ).$$
Hierbei sind $t_0$ und $f_0$ beliebige Zeit– bzw. Frequenzgrößen.
$\text{Beweis von Gleichung (1):}$ Das erste Fourierintegral für das um $t_0$ nach rechts verschobene Signal $x_{\rm V}(t) = x(t-t_0)$ lautet mit der Substitution $\tau = t - t_0$:
- $$X_{\rm V} ( f ) = \int_{ - \infty }^{ + \infty } {x( {t - t_0 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}{\rm d}t} = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}( {\tau + t_0 } )}\hspace{0.1cm} {\rm d}\tau .}$$
Der von der Integrationsvariablen $\tau$ unabhängige Term kann vor das Integral gezogen werden. Mit der Umbennung $\tau \to t$ erhält man dann:
- $$X_{\rm V}( f ) = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot X( f).$$
$\text{Beispiel 6:}$ Wie bereits erwähnt, besitzt der symmetrische Rechteckimpuls $x_1(t)$ das folgende Spektrum:
- $$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ).$$
Der unten dargestellte Rechteckimpuls $x_2(t)$ ist gegenüber $x_1(t)$ um $T/2$ nach rechts verschoben:
- $$x_2(t) = x_1(t-T/2).$$
Somit lautet sein Spektrum:
- $$X_2( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}T} .$$
Diese Spektralfunktion kann mit dem Satz von Euler und einigen einfachen trigonometrischen Umformungen auch wie folgt geschrieben werden:
- $$X_2( f ) = \frac{A }{2\pi f} \cdot \sin ( 2\pi fT) + {\rm j}\cdot \frac{A }{2\pi f} \cdot \big[ {\cos ( {2\pi fT} ) - 1} \big] .$$
Das gleiche Ergebnis erhält man auch mit dem Zuordnungssatz:
- Der Realteil des Spektrums gehört zum geraden Signalanteil $x_{\rm g}(t)$, der Imaginärteil zum ungeraden Anteil $x_{\rm u}(t)$.
Differentiationssatz
Dieser Satz zeigt, wie sich die Differentiation einer Funktion $x(t)$ bzw. $X(f)$ in der korrespondierenden Fouriertransformierten auswirkt; er ist auch mehrfach anwendbar.
Ein einfaches Beispiel für die Anwendung des Differentiationsssatzes ist der Zusammenhang zwischen dem Strom $i(t)$ und der Spannung $u(t)$ einer Kapazität $C$ entsprechend der Gleichung $i(t) = C \cdot \text{d}u(t)/\text{d}t$.
$\text{Differentiationsssatz:}$ Ist $X(f)$ die Fouriertransformierte von $x(t)$, so gelten auch die beiden folgenden Korrespondenzen:
$$\mathbf{(1)}\hspace{0.5cm}\frac{{{\rm d}x( t )}}{{{\rm d}t}}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot X( f ),$$
$$\mathbf{(2)}\hspace{0.5cm}- t \cdot x( t )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}\frac{1}{{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi }} \cdot \frac{{{\rm d}X( f )}}{{{\rm d}f}}.$$
$\text{Beweis von Gleichung (1):}$ Die erste Gleichung ergibt sich durch Differentiation des zweiten Fourierintegrals:
- $$y(t) = \frac{\text{d}x(t)}{\text{d}t} = \frac{\text{d} }{\text{d}t}\int_{ - \infty }^{ + \infty } X( f ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi\hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f = \int_{ - \infty }^{ + \infty } {X( f )} \cdot {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t} {\rm d}f.$$
- Gleichzeitig gilt aber auch:
- $$y( t ) = \int_{ - \infty }^{ + \infty } {Y( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.$$
- Durch Vergleich der Integranden erhält man die Variante $\mathbf{(1)}$ des Differentiationssatzes.
- Zur Herleitung der zweiten Variante geht man ausgehend vom ersten Fourierintegral in analoger Weise vor.
- Der negative Exponent im ersten Fourierintegral führt zum Minuszeichen in der Zeitfunktion. q.e.d.
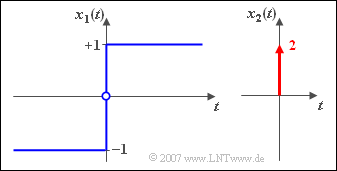
$\text{Beispiel 7:}$ Die Spektren der Signale $x_1(t)$ und $x_2(t)$ wurden bereits in früheren Beispielen wie folgt berechnet:
- $$X_1( f ) = \frac{1 }{ {\rm j\cdot \pi} f}, \hspace{1cm} X_2( f ) = 2 = {\rm const.}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} X_2(f) = X_1(f) \cdot {\rm j}\cdot 2\pi f.$$
- Aus dem Differentiationssatz folgt somit, dass $x_2(t)$ gleich der Ableitung von $x_1(t)$ nach der Zeit ist.
- Dies stimmt tatsächlich: Für $t \neq 0$ ist $x_1(t)$ konstant, also die Ableitung Null.
- Bei $t=0$ ist die Steigung unendlich groß, was sich auch in der Gleichung $x_2(t) = 2 \cdot \delta(t)$ ausdrückt.
- Das Impulsgewicht „2” der Diracfunktion berücksichtigt, dass der Sprung innerhalb der Funktion $x_1(t)$ bei $t = 0$ die Höhe $2$ hat.
Integrationssatz
Die Integration ist ebenso wie die Differentiation eine lineare Operation. Daraus ergibt sich der
$\text{Integrationssatz:}$ Ist $X(f)$ die Fouriertransformierte (Spektralfunktion) von $x(t)$, so gelten auch die folgenden Fourierkorrespondenzen:
$$\mathbf{(1)}\hspace{0.5cm}\int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ X( f )\left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right),$$
$$\mathbf{(2)}\hspace{0.5cm}x( t )\left( { - \frac{1}{{{\rm j}\cdot 2\pi t}} + \frac{1}{2}\cdot \delta ( t )} \right)\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ \int_{ - \infty }^f {X( \nu ) \hspace{0.1cm}{\rm d}\nu .}$$
$\text{Veranschaulichung – kein exakter Beweis:}$
Der Integrationssatz stellt genau die Umkehrung des Differentiationssatzes dar. Wendet man auf die obere Gleichung $\mathbf{(1)}$ den Differentiationssatz an, so erhält man:
- $$\frac{ {\rm d} }{ {\rm d}t} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \ X( f )\cdot \left( {\frac{1}{ { {\rm j}\cdot 2\pi f} } + \frac{1}{2}\cdot \delta ( f )} \right) \cdot {\rm j}\cdot 2\pi f.$$
An diesem Beispiel zeigt sich die Gültigkeit des Integrationssatzes:
- Die Differentiation nach der oberen Grenze auf der linken Seite liefert genau den Integranden $x(t)$.
- Auf der rechten Seite der Korrespondenz ergibt sich richtigerweise $X(f)$, da die Diracfunktion bei $f=0$ wegen der Multiplikation mit $\text{j}\cdot 2\pi f$ ausgeblendet wird.
Hinweis: Alle in diesem Kapitel dargelegten Gesetzmäßigkeiten – unter Anderem auch der Differentiations– und der Integrationssatz – werden im Lernvideo Gesetzmäßigkeiten der Fouriertransformation an Beispielen verdeutlicht.
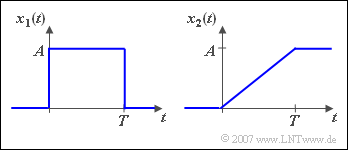
$\text{Beispiel 8:}$ Die skizzierten Signale $x_1(t)$ und $x_2(t)$ hängen wie folgt zusammen:
- $$x_2( t ) = \frac{1}{T}\cdot \int_{ - \infty }^{\hspace{0.05cm}t} {x_1 } ( \tau )\hspace{0.1cm}{\rm d}\tau .$$
Aufgrund des Integrationssatzes gilt dann folgender Zusammenhang zwischen den Spektren:
- $$X_2 ( f ) = \frac{1}{T}\cdot X_1 ( f ) \cdot \left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right).$$
Mit der Spektralfunktion
- $$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT}$$
erhält man somit
- $$X_2 ( f ) = \frac{ {A } }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ {2{\rm j} } } \cdot \frac{ {\sin( {\pi fT}) } }{ {\left( {\pi fT} \right)^2 } } \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT},$$
bzw. nach trigonometrischen Umformungen:
- $$X_2 ( f ) = \frac{ {A} }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ { ( {2\pi fT} )^2 } }\cdot \big[ {\cos( {2\pi fT} ) - 1 - {\rm j}\cdot \sin ( {2\pi ft} )} \big].$$
Hierzu ist anzumerken:
- Die Diracfunktion bei $f = 0$ mit dem Gewicht $A/2$ berücksichtigt den Gleichanteil der Rampenfunktion $x_2(t)$.
- Das bedeutet auch: Der Gleichanteil der Rampenfunktion ist genau so groß wie der Gleichanteil der Sprungfunktion.
- Das fehlende Dreieck mit den Eckpunkt–Koordinaten $(0, 0)$, $(T, A)$ und $(0, A)$ ändert am Gleichanteil nichts.
- Diese Dreieckfläche wirkt sich gegenüber der unendlich großen Restfläche (bis ins Unendliche gehend) nicht aus.
Aufgaben zum Kapitel
Exercise 3.4: Trapezoidal Spectrum and Pulse
Exercise 3.4Z: Trapezoid, Rectangle and Triangle
Exercise 3.5: Differentiation of a Triangular Pulse
Exercise 3.5Z: Integration of Dirac Functions
Exercise 3.6: Even/Odd Time Signal
Exercise 3.6Z: Complex Exponential Function