Difference between revisions of "Signal Representation/The Convolution Theorem and Operation"
| Line 130: | Line 130: | ||
:$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | :$$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | Some more remarks on graphic folding: | |
| − | * | + | *The output value at $t = 0$ is obtained by mirroring the input signal $x(\tau)$ this mirrored signal $x(-\tau)$ is multiplied by the impulse response $h(\tau)$ and integrated above it. |
| − | * | + | *As there is no time interval here, where both the blue curve $h(\tau)$ and at the same time also the red dashed mirroring $x(-\tau)$ is not equal to zero, the result is $y(t=0)=0$. |
| − | * | + | *For any other time $t$ the input signal must be shifted ⇒ $x(t-\tau)$, for example according to the green dotted curve for $t=T$. |
| − | * | + | *As in this example also $x(t-\tau)$ only $0$ and $1$ the integration $($general from $\tau_1$ to $\tau_2)$ is very simple and you get here with $\tau_1 = 0$ and $\tau_2 = t$ : |
:$$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$ | :$$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$ | ||
| − | + | This sketch is valid for $t=T$ and results in the output value $y(t=T) = 1 – 1/\text{e} \approx 0.632$.}} | |
==Clear Interpretation of The Convolution== | ==Clear Interpretation of The Convolution== | ||
<br> | <br> | ||
| − | + | We assume an impulse response $h(t)$ which is first constant for one millisecond and then decreases linearly to zero until $t = 3 \,\text{ms}$ . | |
| − | * | + | *If a Dirac impulse $K_0 \cdot \delta(t)$ is applied to the input of this low-pass filter, the output signal $y(t)$ has the same shape as the impulse response $h(t)$. The situation is shown in red in the picture. |
| − | * | + | *An $T= 1 \,\text{ms}$ shifted Dirac impulse with weight $K_1 > K_0$ results in the output signal $y_1(t)$ which is delayed with respect to the red signal and increased in amplitude. |
[[File:P_ID524__Sig_T_3_4_S5_rah.png|right|frame|On a Clear Interpretation of The Convolution]] | [[File:P_ID524__Sig_T_3_4_S5_rah.png|right|frame|On a Clear Interpretation of The Convolution]] | ||
| − | + | We now consider the input signal consisting of seven differently weighted and shifted Dirac impulses | |
:$$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$ | :$$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$ | ||
| − | + | which can be understood as a time discrete approximation of a time continuous signal. | |
| − | * | + | *The signal at the output of the linear system is the sum of the seven partial signals marked with different colors in the image: |
:$$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$ | :$$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$ | ||
| − | * | + | *We now look at the signal value at time $t = 4.5T$ (see dotted lines): |
:$$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$ | :$$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$ | ||
| − | + | The signal value $y(t=4.5T)$ is thus only determined by the input signal values $K_2$, $K_3$ and $K_4$ the influence | |
| − | * | + | *from $K_4$ due to $h(0.5T) = 1$ at the peak, |
| − | * | + | *from $K_3$ due to $h(1.5T) = 0.75$ less strong, |
| − | * | + | *from $K_2$ due to $h(2.5T) = 0.25$ the lowest. |
| Line 173: | Line 173: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition: }$ | $\text{Definition: }$ | ||
| − | + | The following relation of time functions is called $x_1(t)$ and $x_2(t)$ the '''convolution''' and represents this functional relation with a star: | |
:$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | :$$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | + | This results in the following Fourier correspondence: | |
:$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$}} | :$$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$}} | ||
| Line 184: | Line 184: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Proof: }$ | $\text{Proof: }$ | ||
| − | + | The Fourier integrals of functions $x_1(t)$ and $x_2(t)$ are with modified integration variables: | |
:$$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\tau }\hspace{0.1cm} {\rm{d } }\tau{\rm{,} }$$ | :$$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\tau }\hspace{0.1cm} {\rm{d } }\tau{\rm{,} }$$ | ||
| Line 190: | Line 190: | ||
:$$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t'} ) } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft\hspace{0.05cm}'}\hspace{0.1cm} {\rm{d} }t\hspace{0.05cm}'{\rm{.} }$$ | :$$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t'} ) } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft\hspace{0.05cm}'}\hspace{0.1cm} {\rm{d} }t\hspace{0.05cm}'{\rm{.} }$$ | ||
| − | * | + | *If you form the product of the spectral functions, you get |
:$$X_1 (f) \cdot X_2 (f) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x_1 ( \tau ) \hspace{0.05 cm}\cdot } }\hspace{0.05 cm} x_2 ( {t\hspace{0.05cm}'} ) \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\left( {\tau + t\hspace{0.05cm}'} \right) }\hspace{0.1cm} {\rm d} \tau \hspace{0.1cm}{\rm d}t\hspace{0.05cm}'{\rm{.} }$$ | :$$X_1 (f) \cdot X_2 (f) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x_1 ( \tau ) \hspace{0.05 cm}\cdot } }\hspace{0.05 cm} x_2 ( {t\hspace{0.05cm}'} ) \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\left( {\tau + t\hspace{0.05cm}'} \right) }\hspace{0.1cm} {\rm d} \tau \hspace{0.1cm}{\rm d}t\hspace{0.05cm}'{\rm{.} }$$ | ||
| − | * | + | *With the substitution $t = \tau + t\hspace{0.05cm}'$ results: |
:$$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d } } }\tau \right] } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft}\hspace{0.1cm} {\rm{d} }t{\rm{.} }$$ | :$$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d } } }\tau \right] } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft}\hspace{0.1cm} {\rm{d} }t{\rm{.} }$$ | ||
| − | : | + | :This equation already takes into account that the exponential function is independent of the inner integration variable $τ$ and therefore acts only as a factor of the inner integral. |
| − | * | + | *If we now denote the product of the two spectra with $P(f)$ and the corresponding time function with $p(t)$, the corresponding Fourier integral is |
:$$P(f) = X_1 ( f ) \cdot X_2 ( f ) =\int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft} \hspace{0.1cm}{\rm{d} }t{\rm{.} }$$ | :$$P(f) = X_1 ( f ) \cdot X_2 ( f ) =\int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft} \hspace{0.1cm}{\rm{d} }t{\rm{.} }$$ | ||
| − | * | + | *A coefficient comparison of the two integrals shows that the following relationship must apply: |
:$$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d } }\tau{\rm{.} }$$ | :$$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d } }\tau{\rm{.} }$$ | ||
Revision as of 17:54, 22 November 2020
Contents
Convolution in Time Domain
The „convolution theorem” is one of the most important laws of the Fourier transform, to which an own subchapter is dedicated in this tutorial.
We will first consider the convolution theorem in the time domain and assume that the spectra of two time functions $x_1(t)$ and $x_2(t)$ are known:
- $$X_1 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}x_1( t ),\quad X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}x_2 ( t ).$$
Then for the time function of the product $X_1(f) \cdot X_2(f)$ applies:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Here $\tau$ is a formal integration variable with the dimension of a time.
$\text{Definition:}$ The above connection of the time function $x_1(t)$ and $x_2(t)$ is called convolution and represents this functional connection with a star:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau = x_{\rm{2} } (t) * x_{\rm{1} } (t) .$$
Thus the above Fourier correspondence can be written as follows:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.15cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
The Proof will be shown at the end of the chapter.
Remark: The convolution is commutative ⇒ The order of the operands can be changed: ${ {x}}_{\rm{1}} ( t ) * { {x}}_{\rm{2}} (t ) ={ {x}}_{\rm{2}} ( t ) * { {x}}_{\rm{1}} (t ) $.
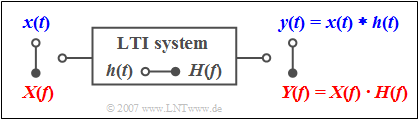
$\text{Example 1:}$ Every linear time-invariant (LTI) system can be described by the frequency response $H(f)$ as well as by the impulse response $h(t)$ where the relation between these two system quantities is also given by the Fourier transform.
If a signal $x(t)$ with the spectrum $X(f)$ is applied to the input, the spectrum of the output signal is:
- $$Y(f) = X(f) \cdot H(f)\hspace{0.05cm}.$$
It is possible to calculate the output signal in the time domain with the convolution theorem:
- $$y( t ) = x(t) * h( t ) = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm}{x( \tau )} \cdot h( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = \int_{ - \infty }^{ + \infty } \hspace{-0.15cm} {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau = h(t) * x( t ).$$
This equation shows again commutativity of the convolution operation.
Convolution in the Frequency Domain
The duality between time and frequency domain also allows statements regarding the spectrum of the product signal:
- $$x_1 ( t ) \cdot x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 (f) * X_2 (f) = \int_{ - \infty }^{ + \infty } {X_1 ( \nu )} \cdot X_2 ( {f - \nu })\hspace{0.1cm}{\rm d}\nu.$$
This result can be proved similarly to the convolution in the time domain . However, the integration variable $\nu$ now has the dimension of a frequency.
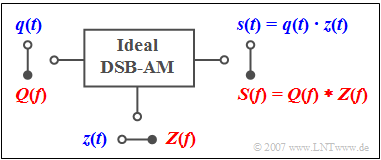
$\text{Example 2:}$ The Double-Sideband Amplitude Modulation (DSB-AM) without a carrier is described by the drawn graph.
- The time domain representation (blue) shows the modulated signal $s(t)$ as the product of the message signal $q(t)$ and the (normalized) carrier signal $z(t)$.
- According to the convolution theorem it follows for the frequency range (red) that the output spectrum $S(f)$ is equal to the convolution product of $Q(f)$ and $Z(f)$ .
Convolution of a Function With a Dirac Function
The convolution operation becomes very simple, if one of the two operands is a Dirac function .This applies equally to the convolution in the time and frequency domain.
We will consider the convolution of a function $x_1(t)$ with the function
- $$x_2 ( t ) = \alpha \cdot \delta ( {t - T} ) \quad \circ\,\!\!\!-\!\!\!-\!\!\!-\!\!\bullet \quad X_2 ( f )= \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$
For the spectral function of the signal $y(t) = x_1(t) \ast x_2(t)$ it follows:
- $$Y( f ) = X_1 ( f ) \cdot X_2 ( f ) = X_1 ( f ) \cdot \alpha \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.05cm}\cdot\hspace{0.05cm}2\hspace{0.03cm}{\rm{\pi }}\hspace{0.05cm}\cdot\hspace{0.05cm}f\hspace{0.05cm}\cdot\hspace{0.05cm}T}.$$
The complex exponential function leads to a shift by $T$ ⇒ Shifting Theorem, the factor $\alpha$ to a damping $(\alpha < 1)$ or amplification $(\alpha > 1)$.
From this follows:
- $$x_1 (t) * x_2 (t) = \alpha \cdot x_1 ( {t - T} ).$$
$\text{In Words: }$ The convolution of any function with a Dirac function at $t = T$ results in the function shifted to the right by $T$ while the weighting of the Dirac function by the factor $\alpha$ has to be taken into account.
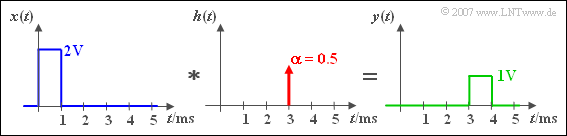
$\text{Example 3:}$ A square wave signal $x(t)$ is delayed by an LTI-system by the delay time $\tau = 3\,\text{ ms}$ and attenuated by the factor $\alpha = 0.5$ .
Shift and attenuation can be recognized by the output signal $y(t)$ as well as by the impulse response $h(t)$.
Graphical Convolution
For the descriptions on this page the following convolution operation is assumed:
- $$y(t) = x_1 (t) * x_2 (t) $$
- $$\Rightarrow \hspace{0.3cm}y(t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
The solution of the convolution integral shall be done graphically. It is assumed that $x_1(t)$ and $x_2(t)$ are continuous time signals.
Then the following steps are required:
- The time variables' of the two functions change:
$x_1(t) \to x_1(\tau)$, $x_2(t) \to x_2(\tau)$. - Mirroring the second function: $x_2(\tau) \to x_2(-\tau)$.
- Shifting the mirrorred function by $t$ $x_2(-\tau) \to x_2(t-\tau)$.
- Multiplication of both functions $x_1(\tau)$ and $x_2(t-\tau)$.
- Integration over the product respective $\tau$ between the limits $-\infty$ to $+\infty$.
Since the convolution is commutative, instead of $x_2(\tau)$ also $x_1(\tau)$ can be mirrored.
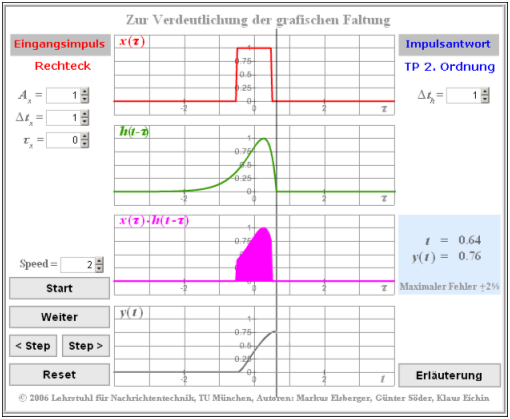
Die Thematik wird auch durch das (neuere) HTML 5–Applet Zur Verdeutlichung der grafischen Faltung veranschaulicht.
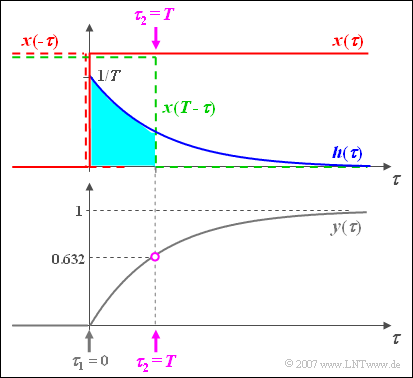
$\text{Example 4:}$ The procedure for the graphic convolution is now explained with a detailed example:
- At the input of a filter there is a jump function $x(t) = \gamma(t)$ .
- The impulse response of the RC low pass filter is $h( t ) = {1}/{T} \cdot {\rm{e} }^{ - t/d}.$
The graphic shows the red colored input signal $x(\tau)$, blue the impulse response $h(\tau)$ and grey the output signal $y(\tau)$.
The time axis is already renamed to $\tau$.
The output signal can be calculated using the following equation, for example:
- $$y(t) = h(t) * x(t) = \int_{ - \infty }^{ + \infty } {h( \tau )} \cdot x( {t - \tau } )\hspace{0.1cm}{\rm d}\tau.$$
Some more remarks on graphic folding:
- The output value at $t = 0$ is obtained by mirroring the input signal $x(\tau)$ this mirrored signal $x(-\tau)$ is multiplied by the impulse response $h(\tau)$ and integrated above it.
- As there is no time interval here, where both the blue curve $h(\tau)$ and at the same time also the red dashed mirroring $x(-\tau)$ is not equal to zero, the result is $y(t=0)=0$.
- For any other time $t$ the input signal must be shifted ⇒ $x(t-\tau)$, for example according to the green dotted curve for $t=T$.
- As in this example also $x(t-\tau)$ only $0$ and $1$ the integration $($general from $\tau_1$ to $\tau_2)$ is very simple and you get here with $\tau_1 = 0$ and $\tau_2 = t$ :
- $$y( t) = \int_0^{\hspace{0.05cm} t} {h( \tau)}\hspace{0.1cm} {\rm d}\tau = \frac{1}{T}\cdot\int_0^{\hspace{0.05cm} t} {{\rm{e}}^{ - \tau /T } }\hspace{0.1cm} {\rm d}\tau = 1 - {{\rm{e}}^{ - t /T } }.$$
This sketch is valid for $t=T$ and results in the output value $y(t=T) = 1 – 1/\text{e} \approx 0.632$.
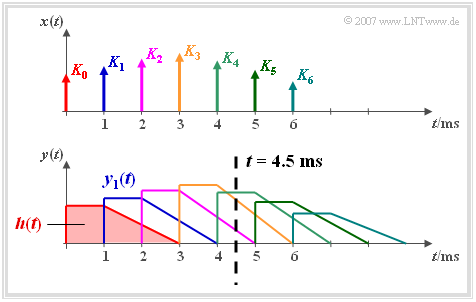
Clear Interpretation of The Convolution
We assume an impulse response $h(t)$ which is first constant for one millisecond and then decreases linearly to zero until $t = 3 \,\text{ms}$ .
- If a Dirac impulse $K_0 \cdot \delta(t)$ is applied to the input of this low-pass filter, the output signal $y(t)$ has the same shape as the impulse response $h(t)$. The situation is shown in red in the picture.
- An $T= 1 \,\text{ms}$ shifted Dirac impulse with weight $K_1 > K_0$ results in the output signal $y_1(t)$ which is delayed with respect to the red signal and increased in amplitude.
We now consider the input signal consisting of seven differently weighted and shifted Dirac impulses
- $$x( t ) = \sum\limits_{n = 0}^6 {K_n \cdot \delta ( {t - n \cdot T} ),}$$
which can be understood as a time discrete approximation of a time continuous signal.
- The signal at the output of the linear system is the sum of the seven partial signals marked with different colors in the image:
- $$y( t ) = \sum\limits_{n = 0}^6 {K_n \cdot h( {t - n \cdot T} ).}$$
- We now look at the signal value at time $t = 4.5T$ (see dotted lines):
- $$y( {t = 4.5T} ) = K_2 \cdot h( {2.5T} ) + K_3 \cdot h(1.5 T ) + K_4 \cdot h( 0.5 T ).$$
The signal value $y(t=4.5T)$ is thus only determined by the input signal values $K_2$, $K_3$ and $K_4$ the influence
- from $K_4$ due to $h(0.5T) = 1$ at the peak,
- from $K_3$ due to $h(1.5T) = 0.75$ less strong,
- from $K_2$ due to $h(2.5T) = 0.25$ the lowest.
Proof of The Convolution Theorem
$\text{Definition: }$ The following relation of time functions is called $x_1(t)$ and $x_2(t)$ the convolution and represents this functional relation with a star:
- $$x_{\rm{1} } (t) * x_{\rm{2} } (t) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau ) } \cdot x_2 ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
This results in the following Fourier correspondence:
- $$X_1 ( f ) \cdot X_2 ( f )\hspace{0.1cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\hspace{0.1cm}{ {x} }_{\rm{1} } ( t ) * { {x} }_{\rm{2} } (t ).$$
$\text{Proof: }$ The Fourier integrals of functions $x_1(t)$ and $x_2(t)$ are with modified integration variables:
- $$X_1 ( f ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\tau }\hspace{0.1cm} {\rm{d } }\tau{\rm{,} }$$
- $$X_2 ( f ) = \int_{ - \infty }^{ + \infty } {x_2 ( {t'} ) } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft\hspace{0.05cm}'}\hspace{0.1cm} {\rm{d} }t\hspace{0.05cm}'{\rm{.} }$$
- If you form the product of the spectral functions, you get
- $$X_1 (f) \cdot X_2 (f) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {x_1 ( \tau ) \hspace{0.05 cm}\cdot } }\hspace{0.05 cm} x_2 ( {t\hspace{0.05cm}'} ) \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }f\left( {\tau + t\hspace{0.05cm}'} \right) }\hspace{0.1cm} {\rm d} \tau \hspace{0.1cm}{\rm d}t\hspace{0.05cm}'{\rm{.} }$$
- With the substitution $t = \tau + t\hspace{0.05cm}'$ results:
- $$X_1 ( f ) \cdot X_2 ( f ) = \int_{ - \infty }^{ + \infty } {\left[ {\int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau} )\hspace{0.1cm}{\rm{d } } }\tau \right] } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft}\hspace{0.1cm} {\rm{d} }t{\rm{.} }$$
- This equation already takes into account that the exponential function is independent of the inner integration variable $τ$ and therefore acts only as a factor of the inner integral.
- If we now denote the product of the two spectra with $P(f)$ and the corresponding time function with $p(t)$, the corresponding Fourier integral is
- $$P(f) = X_1 ( f ) \cdot X_2 ( f ) =\int_{ - \infty }^{ + \infty } {p( t )} \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }ft} \hspace{0.1cm}{\rm{d} }t{\rm{.} }$$
- A coefficient comparison of the two integrals shows that the following relationship must apply:
- $$p( t ) = \int_{ - \infty }^{ + \infty } {x_1 ( \tau )} \cdot x_2 ( {t - \tau } )\hspace{0.1cm}{\rm{d } }\tau{\rm{.} }$$
Exercises for the Chapter
Exercise 3.7: Carrier Recovery
Exercise 3.7Z: Square Wave With Echo
Exercise 3.8: Triple Convolution
Exercise 3.8Z:Convolution of Two Rectangles
Exercise 3.9: Convolution of Rectangle and Gaussian Pulse
Exercise 3.9Z: Convolution of Gaussian Pulses