Difference between revisions of "Aufgaben:Exercise 1.7Z: Overall Systems Analysis"
From LNTwww
| Line 16: | Line 16: | ||
:$$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/T)^2}.$$ | :$$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/T)^2}.$$ | ||
What needs to be investigated is the range in which the equivalent impulse duration $T$ of this Gaussian pulse can vary such that the overall system can be entirely described by the frequency response | What needs to be investigated is the range in which the equivalent impulse duration $T$ of this Gaussian pulse can vary such that the overall system can be entirely described by the frequency response | ||
| − | :$$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_{\rm G})^2}$$ | + | :$$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_{\rm G})^2}.$$ Here, the subscript "G" in frequency response and bandwidth stands for "Gesamtsystem" (German for "overall system"). |
Revision as of 13:20, 8 September 2021
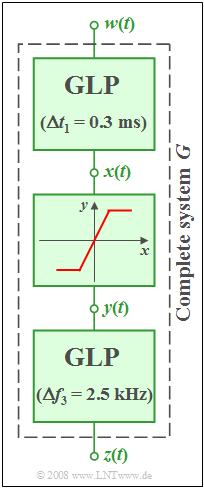
An overall system $G$ with input $w(t)$ and output $z(t)$ consists of three components:
- The first component is a Gaussian low-pass filter with impulse response
- $$h_1(t) = \frac{1}{\Delta t_1} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm} (t/\Delta t_1)^2}, \hspace{0.5cm} \Delta t_1= {0.3\,\rm ms}.$$
- This is then followed by a non-linearity with the characteristic curve
- $$y(t) = \left\{ \begin{array}{c} +{8\,\rm V} \\ 2 \cdot x(t) \\ {-8\,\rm V} \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {x(t) \ge +{4\,\rm V}}, \\ {{-4\,\rm V} < x(t) < +{4\,\rm V}}, \\ {x(t)\le {-4\,\rm V}}. \\ \end{array}$$
- ⇒ The input signal $x(t)$ of the non-linearity is amplified by the factor $2$ and – if necessary – limited to the range $±8 \ \rm V$ .
- At the end of the chain there is again a Gaussian low-pass filter given by its frequency response:
- $$H_3(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_3)^2}, \hspace{0.5cm} \Delta f_3= {2.5\,\rm kHz}.$$
Let the input signal $w(t)$ of the overall system be a Gaussian pulse with amplitude $5 \ \rm V$ and variable (equivalent) duration $T$:
- $$w(t) = {5\,\rm V}\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/T)^2}.$$
What needs to be investigated is the range in which the equivalent impulse duration $T$ of this Gaussian pulse can vary such that the overall system can be entirely described by the frequency response
- $$H_{\rm G}(f) = K \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(f/\Delta f_{\rm G})^2}.$$ Here, the subscript "G" in frequency response and bandwidth stands for "Gesamtsystem" (German for "overall system").
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- Reference is made especially to the page Gaussian low-pass filter.
Questions
Solution
(1) Answers 1 and 3 are correct:
- The first statement is correct: Only for a linear system a frequency response can be specified.
- For this to be possible here nonlinearity must not play a role.
- That is, it must be ensured that $|x(t)|$ is not greater than $4 \ \rm V$ .
- In contrast to this, the second statement is not true: The bandwidth of $H_3(f)$ does not affect whether the non-linearity can be eliminated or not.
(2) The first Gaussian low-pass filter is described in the frequency domain as follows:
- $$X(f) = W(f) \cdot H_1(f) = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f \cdot T)^2} \cdot {\rm e}^{-\pi(f/\Delta f_1)^2} = {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi f^2 (T^2 + \Delta t_1^2)}= {5\,\rm V}\cdot T \cdot {\rm e}^{-\pi(f/\Delta f_x)^2}.$$
- Here, $Δf_x$ denotes the equivalent bandwidth of $X(f)$.
- The signal value at $t = 0$ is equal to the spectral area and at the same time to the maximum value of the signal:
- This should not exceed $4 \ \rm V$:
- $$x_{\rm max} = x(t =0) = {5\,\rm V}\cdot T \cdot \Delta f_x \le {4\,\rm V}.$$
- From this it follows by comparison of coefficients:
- $$\frac{1}{T \cdot \Delta f_x} > \frac{5}{4}\hspace{0.1cm} \Rightarrow \hspace{0.1cm} \frac{1}{T^2 \cdot \Delta f_x^2} > \frac{25}{16} \Rightarrow \hspace{0.3cm}\frac{T^2 + \Delta t_1^2}{T^2} > \frac{25}{16}$$
- $$ \Rightarrow \hspace{0.1cm}\frac{ \Delta t_1^2}{T^2} > \frac{9}{16}\hspace{0.3cm}\Rightarrow \hspace{0.5cm}\frac{T^2}{ \Delta t_1^2} \le \frac{16}{9}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T \le \frac{4}{3} \cdot \Delta t_1 \hspace{0.15cm}\underline{= {0.4\,\rm ms}}.$$
- The control calculation yields:
- $$\Delta t_x = \sqrt{T^2 + \Delta t_1^2} = \sqrt{({0.4\,\rm ms})^2 + ({0.3\,\rm ms})^2} = {0.5\,\rm ms} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_x = {1}/{\Delta t_x}= {2\,\rm kHz}$$
- $$\Rightarrow \hspace{0.3cm} x(t=0) = {5\,\rm V}\cdot T \cdot \Delta f_x = {5\,\rm V}\cdot {0.4\,\rm ms} \cdot {2\,\rm kHz} = {4\,\rm V}.$$
(3) The Gaussian low-pass filters satisfy the condition $H_1(f = 0) = H_3(f = 0) = 1$.
- Taking into account the gain of the second block in the linear domain the following is thus obtained for the total gain:
- $$\underline{K \ = \ 2}.$$
- For the equivalent impulse duration of the overall system it holds that:
- $$\Delta t_{\rm G} = \sqrt{\Delta t_1^2 + \frac{1}{\Delta f_3^2}} = \sqrt{({0.3\,\rm ms})^2 + \left( \frac{1}{{2.5\,\rm kHz}}\right)^2}={0.5\,\rm ms} \; \; \Rightarrow \; \; \Delta f_{\rm G} = {1}/{\Delta t_{\rm G}} \hspace{0.15cm}\underline{= {2\,\rm kHz}}.$$