Aufgaben:Exercise 2.1Z: Distortion and Equalisation

• Return to book

Three continuous spectral functions

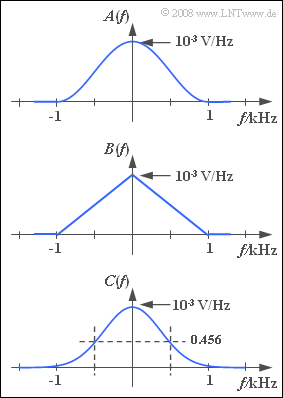
Three continuous spectral functions are depicted in the graph:

• a cos²–spectrum that has components only in the range  $|f| < 1 \ \rm kHz$  where the following holds:

$$A(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \cos^2(\frac{|f|}{1 \, \rm kHz} \cdot \frac{\pi}{ 2} ) ,$$

• a triangular spectrum which is also limited to the frequency range  $|f| < 1 \ \rm kHz$:

$$B(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \left(1-\frac{|f|}{1 \, \rm kHz} \right),$$

• a so-called Gaussian spectrum:

$$C(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot {\rm e}^{-\pi \hspace{0.05cm}\cdot \hspace{0.05cm} (f/{1 \, \rm kHz})^2} .$$

Furthermore, we consider

• a linearly distorting system  $S_{\rm V}$  with  $X(f)$  at the input and  $Y(f)$  at the output, and
• the equalisation system  $S_{\rm E}$  with the input spectrum  $Y(f)$  and output spectrum  $Z(f)$.

The frequency responses of the two systems  $S_{\rm V}$  and  $S_{\rm E}$  are:

$$H_{\rm V}(f) = \frac{Y(f)}{X(f)} , \hspace{0.3cm}$$

$$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} .$$

Please note:

• The exercise belongs to the chapter  Classification of the Distortions.
• A complete equalisation means that  $Z(f) = X(f)$  holds.

Questions

1

Is the constellation $X(f) = A(f)$  and  $Y(f) = B(f)$  possible with a linear system? Justify your answer.

	Yes.
	No.

2

$X(f) = A(f)$  and  $Y(f) = B(f)$ still hold true. Is complete equalisation possible with a linear filter $H_{\rm E}(f)$ ?
If YES, please specify  $H_{\rm E}(f)$.

	Yes.
	No.

3

Is the constellation $X(f) = C(f)$  and  $Y(f) = B(f)$  possible with a linear system? Justify your answer.

	Yes.
	No.

4

$X(f) = C(f)$  und  $Y(f) = B(f)$ still hold true. Is complete equalisation possible with a linear filter $H_{\rm E}(f)$ ?
If YES, please specify  $H_{\rm E}(f)$ .

	Yes.
	No.

5

Is the constellation $X(f) = A(f)$  and  $Y(f) = C(f)$  possible with a linear system?
Justify your answer.

	Yes.
	No.

Solution

Solution

(1)  Yes is correct:

• This constellation is possible because  $X(f)$  is also always different from zero for all  $Y(f) \ne 0$ .
• For all frequencies less than  $0.5 \ \rm kHz$ ,   $H_{\rm V} = B(f)/A(f) < 1$  causes an attenuation.
• In contrast, the frequencies between  $0.5 \ \rm kHz$  and  $1 \ \rm kHz$  are amplified by the system.

(2)  Yes is correct:

• A complete linear equalisation is also possible with this constellation with

$$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} = \frac{A(f)}{B(f)} = \frac{1}{H_{\rm V}(f)}$$

since both spectra extend exactly up to  $1 \ \rm kHz$ .

(3)  Yes is correct:

• This constellation is possible, too. The filter  $H_{\rm V}(f)$  must form a triangular spectrum for the frequencies  $|f| <1 \ \rm kHz$  out of the Gaussian spectrum and suppress all frequencies  $|f| > 1 \ \rm kHz$ .

(4)  No is correct:

• A complete equalisation is not possible here:
• The parts of the Gaussian spectrum, which are completely eliminated by  $H_{\rm V}(f)$ , cannot be recovered by the linear system.

(5)  No is correct:

• This constellation is not possible with a linear system since there cannot be any spectral components in the spectrum  $C(f) = A(f) \cdot H_{\rm V}(f)$  that do not exist in $A(f)$ .
• The question whether there is a non-linear system which forms a Gaussian spectrum out of the  $\cos^2$-spectrum is not asked and therefore does not need to be answered:   The authors rather believe "no".