Aufgaben:Exercise 2.6Z: Synchronous Demodulator

• Return to book

AM–modulator (top) and synchronous demodulator (bottom)

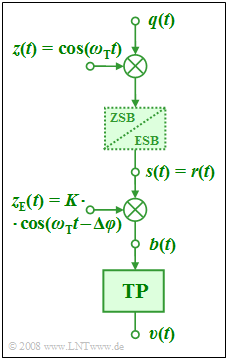
The depicted block diagram shows a transmission system

• with  Double-Sideband Amplitude Modulation  (ZSB-AM)
• and  Synchronous Demodulation (SD).

Let the source signal consist of two harmonic oscillations with frequencies  $f_2 = 2 \ \rm kHz$  and  $f_5 = 5 \ \rm kHz$:

$$q(t) = {2 \, \rm V} \cdot {\rm cos}(\omega_2 t )+ {1 \, \rm V} \cdot {\rm sin}(\omega_5 t ) .$$

• This signal is multiplied by the dimensionless carrier signal  $z(t) = \cos(\omega_{\rm T} \cdot T)$  of frequency  $f_{\rm T} = 50 \ \rm kHz$. For ZSB–AM the dashed block is irrelevant so that the following holds for the transmit signal:

$$s(t) = q(t) \cdot {\rm cos}(\omega_{\rm T} t ) .$$

• In the synchronous demodulator, the receiver signal  $r(t)$  – dentical to the transmit signal  $s(t)$  in an ideal channel – is multiplied by the receive-site carrier signal  $z_{\rm E}(t)$  where the following applies:

$$z_{\rm E}(t) = K \cdot {\rm cos}(\omega_{\rm T} t - \Delta \varphi ) .$$

• This signal should not only be frequency-synchronous with  $z(t)$  but also phase-synchronous – hence the name "synchronous demodulator".
• The above approach takes into account a phase shift between  $z(t)$  and  $z_{\rm E}(t)$, which should ideally be  $\Delta \varphi = 0$  but often cannot be avoided in real systems.

• The output signal  $b(t)$  of the second multiplier includes components around twice the carrier frequency in addition to the desired NF component.
• Using an ideal low-pass filter– for example with cut-off frequency  $f_{\rm T}$  – the sink signal  $v(t)$  can be obtained which ideally should be equal to the source signal  $q(t)$ .

For the transmitter, multiplication by the carrier signal  $z(t)$  generally results in two sidebands. In the  Single-Sideband Modulation  (ESB–AM) only one of the two bands is transmitted, for example the lower sideband (USB). Thus, the following is obtained with an ideal channel:

$$r(t) = s(t)= {1 \, \rm V} \cdot {\rm cos}\big [(\omega_{\rm T} - \omega_2 )\cdot t \big ] - {0.5 \, \rm V} \cdot {\rm sin}\big [(\omega_{\rm T} - \omega_5 )\cdot t \big ] .$$

• Here, synchronous demodulation results in the following distorted sink signal considering a phase shift  $\Delta \varphi$, the constant  $K = 4$  and the downstream low-pass filter:

$$v(t)= {1 \, \rm V} \cdot {1}/{2}\cdot 4 \cdot{\rm cos}( \omega_2 t - \Delta \varphi)+ {0.5 \, \rm V} \cdot {1}/{2}\cdot 4 \cdot{\rm sin}( \omega_5 t - \Delta \varphi)$$

$$\Rightarrow \hspace{0.5cm}v(t)= {2 \, \rm V} \cdot{\rm cos}( \omega_2 t - \Delta \varphi)+ {1 \, \rm V} \cdot{\rm sin}( \omega_5 t - \Delta \varphi)$$

• In the ideal case of phase-synchronous demodulation  $(\Delta \varphi = 0)$,    $v(t) = q(t)$ holds again.

Please note:

• The task belongs to the chapter  Linear Distortions.
• The topic "amplitude modulation/synchronous demodulator" is discussed in detail in the book  Modulation Methods .

• The following trigonometric relationships are given:

$$\cos^2(\alpha) = {1}/{2} \cdot \big [ 1 + \cos(2\alpha) \big ] \hspace{0.05cm}, $$

$$\cos(\alpha) \cdot \cos(\beta) = {1}/{2} \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$

$$ \sin(\alpha) \cdot \cos(\beta) = {1}/{2} \cdot \big[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \big] \hspace{0.05cm}.$$

Questions

1

What is the sink signal $v(t)$  for ZSB-AM and phase-synchronous synchronous modulation  ⇒   $\Delta \varphi = 0$?
How should  $K$  be chosen such that  $v(t) = q(t)$  holds?

$K \ = \ $

2

The following holds:  $K = 2$. Specify the sink signal $v(t)$  considering a phase shift $\Delta \varphi$  an.
Which of the following statements are true?

	$v(t) = q(t)$ holds independently of $\Delta \varphi$ .
	$\Delta \varphi \ne 0$  results in frequency-independent attenuation.
	A phase shift $\Delta \varphi \ne 0$  results in attenuation distortions.
	A phase shift $\Delta \varphi \ne 0$  results in phase distortions.
	$v(t) = q(t)/2$ holds with $\Delta \varphi = \hspace{-0.05cm}-\hspace{0.05cm}60^\circ$ .

3

Which statements hold for synchronous demodulation of the ESB–signal if a phase shift of $\Delta \varphi$  is considered?

	Regardless of $\Delta \varphi$,   $v(t) = q(t)$ holds.
	$\Delta \varphi \ne 0$  results in frequency-independent attenuation.
	A phase shift $\Delta \varphi \ne 0$  results in attenuation distortions.
	A phase shift $\Delta \varphi \ne 0$  results in phase distortions.
	$v(t) = q(t)/2$ holds with $\Delta \varphi = \hspace{-0.05cm}-\hspace{0.05cm}60^\circ$ .

Solution

Solution

(1)  The following holds for the band-pass signal after the second multiplier:

$$b(t) = r(t) \cdot z_{\rm E}(t)= q(t) \cdot z(t) \cdot z_{\rm E}(t)= K \cdot q(t)\cdot \cos^2(\omega_{\rm T} t).$$

• Using the trigonometric relation  $\cos^2(\omega_{\rm T} t) = {1}/{2} \cdot\big[ 1 + \cos(2\omega_{\rm T} t)\big]$, 

$$b(t) = {K}/{2} \cdot q(t) + {K}/{2} \cdot q(t)\cdot \cos(2\omega_{\rm T} t)$$ is obtained.

• Der zweite Anteil liegt um die doppelte Trägerfrequenz   ⇒   $2 f_{\rm T}$. 
• Dieser wird durch den Tiefpass  $($mit der Grenzfrequenz  $ f_{\rm G} = f_{\rm T})$  entfernt.
• Damit erhält man:   $v(t) = {K}/{2} \cdot q(t) .$
• Mit  $\underline {K = 2}$  ergibt sich eine ideale Demodulation   ⇒   $v(t) = q(t)$.

(2)  Unter Berücksichtigung der Beziehung

$$\cos(\omega_{\rm T} t) \cdot \cos(\omega_{\rm T} t - \Delta \varphi) = {1}/{2} \cdot \big[ \cos(\Delta \varphi)+ \cos(2\omega_{\rm T} t - \Delta \varphi) \big]$$

sowie des nachgeschalteten Tiefpasses, der wieder den Anteil um die doppelte Trägerfrequenz entfernt, erhält man hier mit  $ {K = 2}$:

$$v(t) = q(t) \cdot \cos(\Delta \varphi).$$

Richtig sind die Lösungsvorschläge 2 und 5:

• Ein Phasenversatz  $\Delta \varphi$  führt hier nur zu einer frequenzunabhängigen Dämpfung und nicht zu Dämpfungs– oder Phasenverzerrungen.
• Ein Phasenversatz um  $\varphi =\pm 60^\circ$  hat jeweils eine Halbierung des Signals zur Folge.

(3)  Richtig ist hier der Lösungsvorschlag 4.

• Bei beiden Summanden tritt genau der gleiche Phasenversatz  $\Delta \varphi$  auf, und es kommt hier zu Phasenverzerrungen:

$$v(t)= {2 \, \rm V} \cdot{\rm cos}\big[ \omega_2 \cdot (t - \tau_2) \big]+ {1 \, \rm V} \cdot{\rm sin}\big[ \omega_5 t \cdot (t - \tau_5)\big],$$

$${\rm wobei}\hspace{0.5cm}\tau_2 = \frac{\Delta \varphi}{\omega_2} \hspace{0.5cm}\ne \hspace{0.5cm} \tau_5 = \frac{\Delta \varphi}{\omega_5}.$$

• Ein Phasenversatz von  $\varphi =60^\circ$ entsprechend  $\pi/3$  führt hier zu den Verzögerungszeiten:

$$\tau_2 = \frac{\pi/3}{2 \pi \cdot 2\,\,{\rm kHz }} \approx 83.3\,{\rm µ s }, \hspace{0.5cm} \tau_5 = \frac{\pi/3}{2 \pi \cdot 5\,\,{\rm kHz }} \approx 33.3\,{\rm µ s }.$$

• Das niederfrequentere Signal wird also stärker verzögert.