Difference between revisions of "Aufgaben:Exercise 4.4: Conventional Entropy and Differential Entropy"
| Line 3: | Line 3: | ||
}} | }} | ||
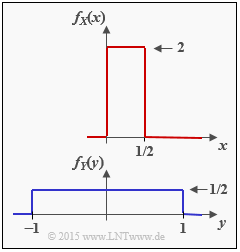
| − | [[File:P_ID2878__Inf_A_4_4.png|right|frame| | + | [[File:P_ID2878__Inf_A_4_4.png|right|frame|Two uniform distributions]] |
| − | + | We consider the two continuous-valued random variables $X$ and $Y$ with probability density functions $f_X(x)$ and $f_Y(y)$. For these random variables one can | |
| − | * | + | * not specify the conventional entropies $H(X)$ and $H(Y)$ , respectively, |
| − | * | + | * but the differential entropies $h(X)$ and $h(Y)$. |
| − | + | We also consider two discrete value random variables: | |
| − | * | + | *The random variable $Z_{X,\hspace{0.05cm}M}$ is obtained by (suitably) quantizing the random variable $X$ with the quantization step number $M$ <br>⇒ quantization interval width ${\it \Delta} = 0.5/M$. |
| − | * | + | * The random quantity $Z_{Y,\hspace{0.05cm}M}$ is obtained after quantization of the random quantity $Y$ with the quantization level number $M$ <br>⇒ quantization interval width ${\it \Delta} = 2/M$. |
| − | + | The probability density functions of these discrete random variables are each composed of $M$ Dirac functions whose momentum weights are given by the interval areas of the associated continuous-value random variables. | |
| − | + | From this, the entropies $H(Z_{X,\hspace{0.05cm}M})$ and $H(Z_{Y,\hspace{0.05cm}M})$ can be determined in the conventional way according to the chapter [[Information_Theory/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Probability_mass_function_and_entropy|Probability Mass Function and Entropy]] . | |
| − | + | In the section [[Information_Theory/Differentielle_Entropie#Entropy_of_value-continuous_random_variables_after_quantization|Entropy of Continuous-Value Random Variables after Quantization]] , an approximation was also given. For example: | |
:$$H(Z_{X, \hspace{0.05cm}M}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X)\hspace{0.05cm}. $$ | :$$H(Z_{X, \hspace{0.05cm}M}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X)\hspace{0.05cm}. $$ | ||
| − | * | + | *In the course of the task it will be shown that in the case of rectangular PDF ⇒ uniform distribution this "approximation" gives the same result as the direct calculation. |
| − | * | + | *But in the general case – so in [[Information_Theory/Differentielle_Entropie#Entropy_of_value-continuous_random_variables_after_quantization|$\text{Example 2}$]] with triangular PDF – above equation is in fact only an approximation, which agrees with the actual entropy $H(Z_{X,\hspace{0.05cm}M})$ only in the limiting case ${\it \Delta} \to 0$ . |
| Line 31: | Line 31: | ||
| − | + | Hints: | |
| − | + | *The exercise belongs to the chapter [[Information_Theory/Differentielle_Entropie|Differential Entropy]]. | |
| − | * | + | *Useful hints for solving this task can be found in particular on the page [[Information_Theory/Differentielle_Entropie#Entropy_of_value-continuous_random_variables_after_quantization|Entropy of continuous-valued random variables after quantization]] . |
| − | * | ||
Revision as of 13:24, 27 September 2021
We consider the two continuous-valued random variables $X$ and $Y$ with probability density functions $f_X(x)$ and $f_Y(y)$. For these random variables one can
- not specify the conventional entropies $H(X)$ and $H(Y)$ , respectively,
- but the differential entropies $h(X)$ and $h(Y)$.
We also consider two discrete value random variables:
- The random variable $Z_{X,\hspace{0.05cm}M}$ is obtained by (suitably) quantizing the random variable $X$ with the quantization step number $M$
⇒ quantization interval width ${\it \Delta} = 0.5/M$. - The random quantity $Z_{Y,\hspace{0.05cm}M}$ is obtained after quantization of the random quantity $Y$ with the quantization level number $M$
⇒ quantization interval width ${\it \Delta} = 2/M$.
The probability density functions of these discrete random variables are each composed of $M$ Dirac functions whose momentum weights are given by the interval areas of the associated continuous-value random variables.
From this, the entropies $H(Z_{X,\hspace{0.05cm}M})$ and $H(Z_{Y,\hspace{0.05cm}M})$ can be determined in the conventional way according to the chapter Probability Mass Function and Entropy .
In the section Entropy of Continuous-Value Random Variables after Quantization , an approximation was also given. For example:
- $$H(Z_{X, \hspace{0.05cm}M}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X)\hspace{0.05cm}. $$
- In the course of the task it will be shown that in the case of rectangular PDF ⇒ uniform distribution this "approximation" gives the same result as the direct calculation.
- But in the general case – so in $\text{Example 2}$ with triangular PDF – above equation is in fact only an approximation, which agrees with the actual entropy $H(Z_{X,\hspace{0.05cm}M})$ only in the limiting case ${\it \Delta} \to 0$ .
Hints:
- The exercise belongs to the chapter Differential Entropy.
- Useful hints for solving this task can be found in particular on the page Entropy of continuous-valued random variables after quantization .
Fragebogen
Musterlösung
- $$h(X) = {\rm log}_2 \hspace{0.1cm} (x_{\rm max} - x_{\rm min}) = {\rm log}_2 \hspace{0.1cm} (1/2) \hspace{0.15cm}\underline{= - 1\,{\rm bit}}\hspace{0.05cm}.$$
(2) Mit $y_{\rm min} = -1$ und $y_{\rm max} = +1$ ergibt sich dagegen für die differentielle Entropie der Zufallsgröße $Y$:
- $$h(Y) = {\rm log}_2 \hspace{0.1cm} (y_{\rm max} - y_{\rm min}) = {\rm log}_2 \hspace{0.1cm} (2) \hspace{0.15cm}\underline{= + 1\,{\rm bit}}\hspace{0.05cm}. $$
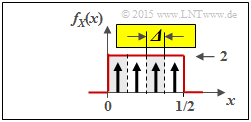
(3) Die nebenstehende Grafik verdeutlicht die bestmögliche Quantisierung der Zufallsgröße $X$ mit der Quantisierungsstufenzahl $M = 4$ ⇒ Zufallsgröße $Z_{X, \ M = 4}$:
- Die Intervallbreite ist hier gleich ${\it \Delta} = 0.5/4 = 1/8$.
- Die möglichen Werte (jeweils in der Intervallmitte) sind $z \in \{0.0625,\ 0.1875,\ 0.3125,\ 0.4375\}$.
Die direkte Entropieberechnung ergibt mit der Wahrscheinlichkeitsfunktion $P_Z(Z) = \big [1/4,\ \text{...} , \ 1/4 \big]$:
- $$H(Z_{X, \ M = 4}) = {\rm log}_2 \hspace{0.1cm} (4) \hspace{0.15cm}\underline{= 2\,{\rm bit}} \hspace{0.05cm}.$$
Mit der Näherung erhält man unter Berücksichtigung des Ergebnisses von (1):
- $$H(Z_{X,\hspace{0.05cm} M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X) = 3\,{\rm bit} +(- 1\,{\rm bit})\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}. $$
Hinweis: Nur bei der Gleichverteilung liefert die Näherung genau das gleiche Ergebnis wie die direkte Berechnung, also die tatsächliche Entropie.
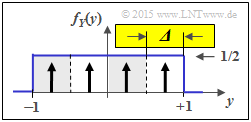
(4) Aus der zweiten Grafik erkennt man die Gemeinsamkeiten / Unterschiede zur Teilaufgabe (3):
- Der Quantisierungsparameter ist nun ${\it \Delta} = 2/4 = 1/2$.
- Die möglichen Werte sind nun $z \in \{\pm 0.75,\ \pm 0.25\}$.
- Somit liefert hier die "Näherung" (ebenso wie die direkte Berechnung) das Ergebnis:
- $$H(Z_{Y,\hspace{0.05cm} M = 4}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y) = 1\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 2\,{\rm bit}}\hspace{0.05cm}.$$
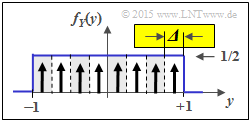
(5) Im Gegensatz zur Teilaufgabe (5) gilt nun ${\it \Delta} = 1/4$. Daraus folgt für die "Näherung":
- $$H(Z_{Y,\hspace{0.05cm} M = 8}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(Y) = 2\,{\rm bit} + 1\,{\rm bit}\hspace{0.15cm}\underline{= 3\,{\rm bit}}\hspace{0.05cm}.$$
Man erhält wieder das gleiche Ergebnis wie bei der direkten Berechnung.
(6) Richtig ist nur die Aussage 1:
- Die Entropie $H(Z)$ einer diskreten Zufallsgröße $Z = \{z_1, \ \text{...} \ , z_M\}$ ist nie negativ.
- Der Grenzfall $H(Z) = 0$ ergibt sich zum Beispiel für ${\rm Pr}(Z = z_1) = 1$ und ${\rm Pr}(Z = z_\mu) = 0$ für $2 \le \mu \le M$.
- Dagegen kann die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße $X$ wie folgt sein:
- $h(X) < 0$ $($Teilaufgabe 1$)$,
- $h(X) > 0$ $($Teilaufgabe 2$)$, oder auch
- $h(X) = 0$ $($zum Beispiel für $x_{\rm min} = 0$ und $x_{\rm max} = 1)$.