Difference between revisions of "Linear and Time Invariant Systems/Properties of Coaxial Cables"
m (Text replacement - "”" to """) |
|||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Properties of Electrical Cables |
| − | |Vorherige Seite= | + | |Vorherige Seite=Some Results from Line Transmission Theory |
| − | |Nächste Seite= | + | |Nächste Seite=Properties of Balanced Copper Pairs |
}} | }} | ||
| − | == | + | ==Complex propagation function of coaxial cables== |
<br> | <br> | ||
| − | + | Coaxial cables consist of an inner conductor and - separated by a dielectric - an outer conductor. Two different types of cable have been standardized, with the diameters of the inner and outer conductors mentioned for identification purposes: | |
| − | * | + | *the ''standard coaxial cable'' whose inner conductor has a diameter of $\text{2.6 mm}$ and whose outer diameter is $\text{9.5 mm}$ , |
| − | * | + | *the ''small coaxial cable'' with dimensions $\text{1.2 mm}$ and $\text{4.4 mm}$. |
| − | + | The cable frequency response $H_{\rm K}(f)$ results from the cable length $l$ and the complex propagation function (per unit length) | |
:$$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot (\beta_1 \cdot f + \beta_2 \cdot \sqrt {f})\hspace{0.05cm}\hspace{0.3cm} | :$$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot (\beta_1 \cdot f + \beta_2 \cdot \sqrt {f})\hspace{0.05cm}\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{-\gamma(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{-\alpha(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l}\hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{-\gamma(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{-\alpha(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l}\hspace{0.05cm}.$$ | ||
| − | + | The cable specific constants for the '''standard coaxial cable''' $\text{(2.6/9.5 mm)}$ are: | |
:$$\begin{align*}\alpha_0 & = 0.00162\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000435\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.2722\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 21.78\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$ | :$$\begin{align*}\alpha_0 & = 0.00162\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000435\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.2722\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 21.78\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$ | ||
| − | + | Accordingly, the kilometric attenuation and phase constants for the '''small coaxial cable''' $\text{(1.2/4.4 mm)}$: | |
:$$\begin{align*}\alpha_0 & = 0.00783\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} | :$$\begin{align*}\alpha_0 & = 0.00783\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} | ||
\alpha_1 = 0.000443\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.5984\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 22.18\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.5984\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$ | \alpha_1 = 0.000443\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.5984\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 22.18\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.5984\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$ | ||
| − | + | These values can be calculated from the geometric dimensions of the cables and have been confirmed by measurements at the Fernmeldetechnisches Zentralamt in Darmstadt - see [Wel77]<ref>Wellhausen, H. W.: ''Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren''. Frequenz 31, S. 23-28, 1977.</ref>. They apply to a temperature of $20^\circ\ \text{C (293 K)}$ and frequencies greater than $\text{200 kHz}$. | |
| − | + | There is the following connection to the [[Linear_and_Time_Invariant_Systems/Some_Results_from_Line_Transmission_Theory#Equivalent_circuit_diagram_of_a_short_transmission_line_section|primary line parameters]]: | |
| − | * | + | *The ohmic losses originating from the frequency-independent component $R\hspace{0.05cm}'$ are modeled by the parameter $α_0$ and cause a (small for coaxial cables) frequency-independent attenuation. |
| − | * | + | *The component $α_1 · f$ of the attenuation function (per unit length) is due to the derivation losses $(G\hspace{0.08cm}’)$ and the frequency-proportional term $β_1 · f$ causes only delay but no distortion. |
| − | * | + | *The components $α_2$ and $β_2$ are due to the [[Digital_Signal_Transmission/Ursachen_und_Auswirkungen_von_Impulsinterferenzen#Frequenzgang_eines_Koaxialkabels|skin effect]], which causes the current density inside the conductor to be lower than at the surface in the case of higher-frequency alternating current. As a result, the serial resistance (per unit length) $R\hspace{0.05cm}’$ of an electric line increases with the square root of the frequency. |
| − | == | + | ==Characteristic cable attenuation== |
<br> | <br> | ||
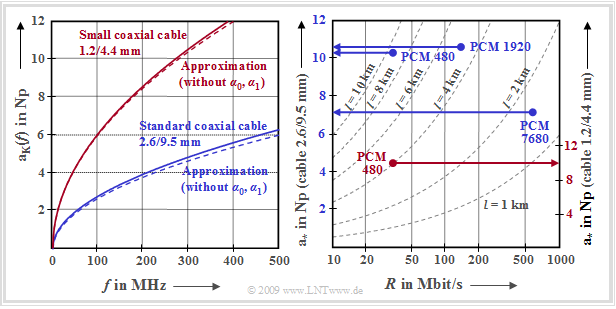
| − | + | The graph shows the frequency-dependent attenuation curve for the normal coaxial cable and the small coaxial cable. Shown on the left is the cable attenuation of the two coaxial cable types in the frequency range up to $\text{500 MHz}$: | |
| − | [[File:EN_LZI_4_2_S2.png |right|frame| | + | [[File:EN_LZI_4_2_S2.png |right|frame| Attenuation function and characteristic attenuation of coaxial cables]] |
:$${\rm a}_{\rm K}(f) \hspace{-0.05cm} = \hspace{-0.05cm}\big [ \alpha_0 \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_1 \cdot f \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_2 \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt {f} \hspace{0.01cm} \hspace{0.1cm} \big ] \cdot l \hspace{0.01cm}.$$ | :$${\rm a}_{\rm K}(f) \hspace{-0.05cm} = \hspace{-0.05cm}\big [ \alpha_0 \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_1 \cdot f \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_2 \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt {f} \hspace{0.01cm} \hspace{0.1cm} \big ] \cdot l \hspace{0.01cm}.$$ | ||
| − | '' | + | ''Notes on graphical representation:'' |
| − | * | + | *The ordinate labeling is given here in "Np/km". |
| − | * | + | *Often it is also expressed with "dB/km", where the following conversion applies:<br> $1 \ \rm dB = 0.11513\text{... Np}$, since $\ln(10)/20 = 0.11513\text{...}$ |
| − | * | + | *The attenuation curve is here labeled ${\rm a}_{\rm K}(f)$ rather than ${a}_{\rm K}(f)$ ⇒ ''italicized'' to make the difference between the attenuation function per unit length „alpha” and the attenuation function „a” (after multiplication with length) more apparent. |
<br clear=all> | <br clear=all> | ||
| − | + | It can be seen from the left graph that the error is still tolerable if the frequency-independent component $α_0$ and the frequency-proportional term $(α_1\cdot f)$ are neglected. In the following, we therefore assume the following simplified attenuation function: | |
:$${\rm a}_{\rm K}(f) = \alpha_2 \cdot \sqrt {f} \cdot l = {\rm a}_{\rm \star}\cdot \sqrt | :$${\rm a}_{\rm K}(f) = \alpha_2 \cdot \sqrt {f} \cdot l = {\rm a}_{\rm \star}\cdot \sqrt | ||
{ {2f}/{R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{- {\rm a}_{\rm K}(f)}\hspace{0.05cm}, \hspace{0.2cm} {\rm a}_{\rm K}(f)\hspace{0.15cm}{\rm in }\hspace{0.15cm}{\rm Np}\hspace{0.05cm}.$$ | { {2f}/{R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{- {\rm a}_{\rm K}(f)}\hspace{0.05cm}, \hspace{0.2cm} {\rm a}_{\rm K}(f)\hspace{0.15cm}{\rm in }\hspace{0.15cm}{\rm Np}\hspace{0.05cm}.$$ | ||
| Line 52: | Line 52: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | We denote the '''characteristic cable attenuation''' $\rm a_∗$ as the attenuation of a coaxial cable at half the bit rate neglecting the terms $α_0$ and $α_1$: | |
:$${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f = {R}/{2}) = \alpha_2 \cdot \sqrt {{R}/{2}} \cdot l\hspace{0.05cm}.$$ | :$${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f = {R}/{2}) = \alpha_2 \cdot \sqrt {{R}/{2}} \cdot l\hspace{0.05cm}.$$ | ||
| − | + | This value is particularly suitable for comparing different conducted transmission systems with different | |
| − | * | + | *coaxial cable types (for example, normal or small coaxial cable), each identified by the parameter $\alpha_2$, |
| − | * | + | *bit rates $(R)$ and |
| − | * | + | *cable lengths $(l)$.}} |
| − | + | The right diagram shows the characteristic cable attenuation $\rm a_∗$ in "Neper" (Np) as a function of the bit rate $R$ and the cable length $l$ | |
| − | * | + | *for the normal coaxial cable (left ordinate labeling) and |
| − | * | + | *for the small coaxial cable (right ordinate labeling). |
| − | + | This diagram shows the PCM systems of hierarchy levels $3$ to $5$ proposed by the [https://en.wikipedia.org/wiki/ITU-T ITU-T] (''ITU Telecommunication Standardization Sector'') in the 1970s. One recognizes: | |
| − | * | + | *For all these systems for PCM speech transmission, the characteristic cable attenuation assumes values between $7 \ \rm Np \ \ (≈ 61 \ dB)$ and $10.6 \ \rm Np \ \ (≈ 92 \ dB)$ . |
| − | * | + | *The system $\text{PCM 480}$ – designed for 480 simultaneous telephone calls - with the bit rate $R ≈ 35 \ \rm Mbit/s$ was specified for both the normal coaxial cable $($with $l = 9.3 \ \rm km)$ and for the small coaxial cable $($with $l = 4 \ \rm km)$ specified. The $\rm a_∗$values $10.4\ \rm Np$ and $9.9\ \rm Np$ respectively are in the same order of magnitude. |
| − | * | + | *The transmission system $\text{PCM 1920}$ of the fourth hierarchy level (specified for the normal coaxial cable) with $R ≈ 140 \ \rm Mbit/s$ and $l = 4.65 \ \rm km$ is parameterized by $\rm a_∗ = 10.6 \ \rm Np$ or $10.6 \ {\rm Np}· 8.688 \ \rm dB/Np ≈ 92\ \rm dB$ . |
| − | * | + | *Although the system $\text{PCM 7680}$ in contrast has four times the capacity $R ≈ 560 \rm Mbit/s$ , the characteristic cable attenuation of $\rm a_∗ ≈ 61 \ dB$ due to the better medium "normal coaxial cable" and the shorter cable sections by a factor of $3$ $(l = 1. 55 \ \rm km)$ significantly lower. |
| − | * | + | *These numerical values also show that for coaxial cable systems, the cable length $l$ is more critical than the bit rate $R$. If one wants to double the cable length, one has to reduce the bit rate by a factor $4$ . |
| − | + | You can view the topic described here with the interactive applet [[Applets:Dämpfung_von_Kupferkabeln|Attenuation of copper cables]] . | |
| − | == | + | ==Impulse response of a coaxial cable== |
<br> | <br> | ||
| − | + | To calculate the impulse response, the first two attenuation components of the five components of the complex propagation function (per unit length) can be neglected (the reasoning can be found in the previous section). So we start from the following equation: | |
:$$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \approx {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \hspace{0.05cm}.$$ | :$$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \approx {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \hspace{0.05cm}.$$ | ||
| − | + | Considering | |
| − | * | + | *the cable length $l$, |
| − | * | + | *the characteristic cable attenuation $\rm a_∗$ and |
| − | * | + | *that $α_2$ (in Np) and $β_2$ (in rad) are numerically equal, |
| − | + | thus applies to the frequency response of the coaxial cable: | |
:$$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.05cm} \sqrt{2f/R} }\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.02cm} \sqrt{2f/R}}= {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R}} \hspace{0.05cm}.$$ | :$$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.05cm} \sqrt{2f/R} }\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.02cm} \sqrt{2f/R}}= {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R}} \hspace{0.05cm}.$$ | ||
| − | + | The following abbreviations are used here: | |
:$$b_1\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm rad)}= \beta_1 \cdot l \hspace{0.05cm}, \hspace{0.8cm} {\rm a}_{\rm \star}\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm Np)}= \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}.$$ | :$$b_1\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm rad)}= \beta_1 \cdot l \hspace{0.05cm}, \hspace{0.8cm} {\rm a}_{\rm \star}\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm Np)}= \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}.$$ | ||
| − | + | The time domain display is obtained by applying the [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|Fourier inverse transform]] and the [[Signal_Representation/The_Convolution_Theorem_and_Operation|Convolution theorem]]: | |
:$$h_{\rm K}(t) = \mathcal{F}^{-1} \left \{ {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 | :$$h_{\rm K}(t) = \mathcal{F}^{-1} \left \{ {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 | ||
f}\right \} \star\mathcal{F}^{-1} \left \{ {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R} }\right \} \hspace{0.05cm}.$$ | f}\right \} \star\mathcal{F}^{-1} \left \{ {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R} }\right \} \hspace{0.05cm}.$$ | ||
| − | + | To be considered here: | |
| − | * | + | *The first term yields the Dirac function $δ(t – τ_{\rm P})$ shifted by the phase delay $τ_{\rm P} = b_1/2π$ . |
| − | * | + | *The second term can be given analytically closed. We write $h_{\rm K}(t + τ_P)$, so that the phase delay $τ_{\rm P}$ need not be considered further. |
:$$h_{\rm K}(t + \tau_{\rm P}) = \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \cdot R \cdot t^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \cdot R\cdot t}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$ | :$$h_{\rm K}(t + \tau_{\rm P}) = \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \cdot R \cdot t^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \cdot R\cdot t}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$ | ||
| − | * | + | *Since also the bit rate $R$ has already been considered in the definition of the characteristic cable attenuation $a_∗$ this equation can be easily represented with the normalized time $t\hspace{0.05cm}' = t/T$ : |
:$$h_{\rm K}(t\hspace{0.05cm}' + \tau_{\rm P}\hspace{0.05cm} ') = \frac {1}{T} \cdot \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \cdot t\hspace{0.05cm}'\hspace{0.05cm}^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \cdot t\hspace{0.05cm}'}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$ | :$$h_{\rm K}(t\hspace{0.05cm}' + \tau_{\rm P}\hspace{0.05cm} ') = \frac {1}{T} \cdot \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \cdot t\hspace{0.05cm}'\hspace{0.05cm}^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \cdot t\hspace{0.05cm}'}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$ | ||
| − | : | + | :Here $T = 1/R$ denotes the symbol duration of a binary system and it holds $τ_{\rm P} \hspace{0.05cm}' = τ_{\rm P}/T$. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | The results of this page are illustrated by the following graph as an example. | |
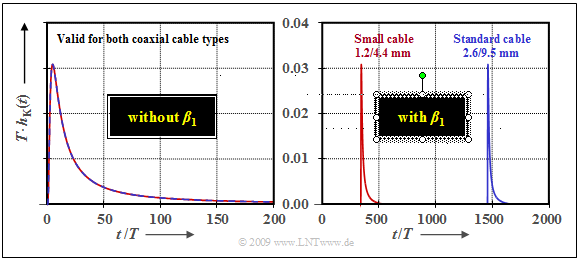
| − | * | + | *The normalized impulse response $T · h_{\rm K}(t)$ of a coaxial cable with $\rm a_∗ = 60 \ dB \ \ (6.9\ Np)$ is shown. |
| − | * | + | *The attenuation function parameters $α_0$ and $α_1$ are thus neglected. |
| − | * | + | *For the left graph, the parameter $β_1 = 0$ was also set. |
| − | [[File:EN_LZI_4_2_S3.png|center|frame| | + | [[File:EN_LZI_4_2_S3.png|center|frame| Impulse response of a coaxial cable with $\rm a_∗ = 60 \ dB$]] |
| − | + | Due to the parameterization by means of the characteristic cable attenuation $a_∗$ and the normalization of the time to the symbol duration $T$ the left curve is equally valid for systems with small or normal coaxial cable, different lengths and different bit rates, for example for a | |
| − | * | + | *normal coaxial cable $\text{2.6/9.5 mm}$, bit rate $R = 140 \ \rm Mbit/s$, cable length $l = 3 \ \rm km$ ⇒ system $\rm A$, |
| − | * | + | *small coaxial cable $\text{1.2/4.4 mm mm}$, bit rate $R = 35 \ \rm Mbit/s$, cable length $l = 2.8 \ \rm km$ ⇒ system $\rm B$. |
Revision as of 11:50, 8 November 2021
Contents
Complex propagation function of coaxial cables
Coaxial cables consist of an inner conductor and - separated by a dielectric - an outer conductor. Two different types of cable have been standardized, with the diameters of the inner and outer conductors mentioned for identification purposes:
- the standard coaxial cable whose inner conductor has a diameter of $\text{2.6 mm}$ and whose outer diameter is $\text{9.5 mm}$ ,
- the small coaxial cable with dimensions $\text{1.2 mm}$ and $\text{4.4 mm}$.
The cable frequency response $H_{\rm K}(f)$ results from the cable length $l$ and the complex propagation function (per unit length)
- $$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot (\beta_1 \cdot f + \beta_2 \cdot \sqrt {f})\hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{-\gamma(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{-\alpha(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l}\hspace{0.05cm}.$$
The cable specific constants for the standard coaxial cable $\text{(2.6/9.5 mm)}$ are:
- $$\begin{align*}\alpha_0 & = 0.00162\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000435\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.2722\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 21.78\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$
Accordingly, the kilometric attenuation and phase constants for the small coaxial cable $\text{(1.2/4.4 mm)}$:
- $$\begin{align*}\alpha_0 & = 0.00783\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000443\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.5984\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 22.18\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.5984\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$
These values can be calculated from the geometric dimensions of the cables and have been confirmed by measurements at the Fernmeldetechnisches Zentralamt in Darmstadt - see [Wel77][1]. They apply to a temperature of $20^\circ\ \text{C (293 K)}$ and frequencies greater than $\text{200 kHz}$.
There is the following connection to the primary line parameters:
- The ohmic losses originating from the frequency-independent component $R\hspace{0.05cm}'$ are modeled by the parameter $α_0$ and cause a (small for coaxial cables) frequency-independent attenuation.
- The component $α_1 · f$ of the attenuation function (per unit length) is due to the derivation losses $(G\hspace{0.08cm}’)$ and the frequency-proportional term $β_1 · f$ causes only delay but no distortion.
- The components $α_2$ and $β_2$ are due to the skin effect, which causes the current density inside the conductor to be lower than at the surface in the case of higher-frequency alternating current. As a result, the serial resistance (per unit length) $R\hspace{0.05cm}’$ of an electric line increases with the square root of the frequency.
Characteristic cable attenuation
The graph shows the frequency-dependent attenuation curve for the normal coaxial cable and the small coaxial cable. Shown on the left is the cable attenuation of the two coaxial cable types in the frequency range up to $\text{500 MHz}$:
- $${\rm a}_{\rm K}(f) \hspace{-0.05cm} = \hspace{-0.05cm}\big [ \alpha_0 \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_1 \cdot f \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_2 \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt {f} \hspace{0.01cm} \hspace{0.1cm} \big ] \cdot l \hspace{0.01cm}.$$
Notes on graphical representation:
- The ordinate labeling is given here in "Np/km".
- Often it is also expressed with "dB/km", where the following conversion applies:
$1 \ \rm dB = 0.11513\text{... Np}$, since $\ln(10)/20 = 0.11513\text{...}$
- The attenuation curve is here labeled ${\rm a}_{\rm K}(f)$ rather than ${a}_{\rm K}(f)$ ⇒ italicized to make the difference between the attenuation function per unit length „alpha” and the attenuation function „a” (after multiplication with length) more apparent.
It can be seen from the left graph that the error is still tolerable if the frequency-independent component $α_0$ and the frequency-proportional term $(α_1\cdot f)$ are neglected. In the following, we therefore assume the following simplified attenuation function:
- $${\rm a}_{\rm K}(f) = \alpha_2 \cdot \sqrt {f} \cdot l = {\rm a}_{\rm \star}\cdot \sqrt { {2f}/{R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{- {\rm a}_{\rm K}(f)}\hspace{0.05cm}, \hspace{0.2cm} {\rm a}_{\rm K}(f)\hspace{0.15cm}{\rm in }\hspace{0.15cm}{\rm Np}\hspace{0.05cm}.$$
$\text{Definition:}$ We denote the characteristic cable attenuation $\rm a_∗$ as the attenuation of a coaxial cable at half the bit rate neglecting the terms $α_0$ and $α_1$:
- $${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f = {R}/{2}) = \alpha_2 \cdot \sqrt {{R}/{2}} \cdot l\hspace{0.05cm}.$$
This value is particularly suitable for comparing different conducted transmission systems with different
- coaxial cable types (for example, normal or small coaxial cable), each identified by the parameter $\alpha_2$,
- bit rates $(R)$ and
- cable lengths $(l)$.
The right diagram shows the characteristic cable attenuation $\rm a_∗$ in "Neper" (Np) as a function of the bit rate $R$ and the cable length $l$
- for the normal coaxial cable (left ordinate labeling) and
- for the small coaxial cable (right ordinate labeling).
This diagram shows the PCM systems of hierarchy levels $3$ to $5$ proposed by the ITU-T (ITU Telecommunication Standardization Sector) in the 1970s. One recognizes:
- For all these systems for PCM speech transmission, the characteristic cable attenuation assumes values between $7 \ \rm Np \ \ (≈ 61 \ dB)$ and $10.6 \ \rm Np \ \ (≈ 92 \ dB)$ .
- The system $\text{PCM 480}$ – designed for 480 simultaneous telephone calls - with the bit rate $R ≈ 35 \ \rm Mbit/s$ was specified for both the normal coaxial cable $($with $l = 9.3 \ \rm km)$ and for the small coaxial cable $($with $l = 4 \ \rm km)$ specified. The $\rm a_∗$values $10.4\ \rm Np$ and $9.9\ \rm Np$ respectively are in the same order of magnitude.
- The transmission system $\text{PCM 1920}$ of the fourth hierarchy level (specified for the normal coaxial cable) with $R ≈ 140 \ \rm Mbit/s$ and $l = 4.65 \ \rm km$ is parameterized by $\rm a_∗ = 10.6 \ \rm Np$ or $10.6 \ {\rm Np}· 8.688 \ \rm dB/Np ≈ 92\ \rm dB$ .
- Although the system $\text{PCM 7680}$ in contrast has four times the capacity $R ≈ 560 \rm Mbit/s$ , the characteristic cable attenuation of $\rm a_∗ ≈ 61 \ dB$ due to the better medium "normal coaxial cable" and the shorter cable sections by a factor of $3$ $(l = 1. 55 \ \rm km)$ significantly lower.
- These numerical values also show that for coaxial cable systems, the cable length $l$ is more critical than the bit rate $R$. If one wants to double the cable length, one has to reduce the bit rate by a factor $4$ .
You can view the topic described here with the interactive applet Attenuation of copper cables .
Impulse response of a coaxial cable
To calculate the impulse response, the first two attenuation components of the five components of the complex propagation function (per unit length) can be neglected (the reasoning can be found in the previous section). So we start from the following equation:
- $$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \approx {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \hspace{0.05cm}.$$
Considering
- the cable length $l$,
- the characteristic cable attenuation $\rm a_∗$ and
- that $α_2$ (in Np) and $β_2$ (in rad) are numerically equal,
thus applies to the frequency response of the coaxial cable:
- $$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.05cm} \sqrt{2f/R} }\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.02cm} \sqrt{2f/R}}= {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R}} \hspace{0.05cm}.$$
The following abbreviations are used here:
- $$b_1\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm rad)}= \beta_1 \cdot l \hspace{0.05cm}, \hspace{0.8cm} {\rm a}_{\rm \star}\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm Np)}= \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}.$$
The time domain display is obtained by applying the Fourier inverse transform and the Convolution theorem:
- $$h_{\rm K}(t) = \mathcal{F}^{-1} \left \{ {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f}\right \} \star\mathcal{F}^{-1} \left \{ {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R} }\right \} \hspace{0.05cm}.$$
To be considered here:
- The first term yields the Dirac function $δ(t – τ_{\rm P})$ shifted by the phase delay $τ_{\rm P} = b_1/2π$ .
- The second term can be given analytically closed. We write $h_{\rm K}(t + τ_P)$, so that the phase delay $τ_{\rm P}$ need not be considered further.
- $$h_{\rm K}(t + \tau_{\rm P}) = \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \cdot R \cdot t^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \cdot R\cdot t}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$
- Since also the bit rate $R$ has already been considered in the definition of the characteristic cable attenuation $a_∗$ this equation can be easily represented with the normalized time $t\hspace{0.05cm}' = t/T$ :
- $$h_{\rm K}(t\hspace{0.05cm}' + \tau_{\rm P}\hspace{0.05cm} ') = \frac {1}{T} \cdot \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \cdot t\hspace{0.05cm}'\hspace{0.05cm}^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \cdot t\hspace{0.05cm}'}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$
- Here $T = 1/R$ denotes the symbol duration of a binary system and it holds $τ_{\rm P} \hspace{0.05cm}' = τ_{\rm P}/T$.
$\text{Example 1:}$ The results of this page are illustrated by the following graph as an example.
- The normalized impulse response $T · h_{\rm K}(t)$ of a coaxial cable with $\rm a_∗ = 60 \ dB \ \ (6.9\ Np)$ is shown.
- The attenuation function parameters $α_0$ and $α_1$ are thus neglected.
- For the left graph, the parameter $β_1 = 0$ was also set.
Due to the parameterization by means of the characteristic cable attenuation $a_∗$ and the normalization of the time to the symbol duration $T$ the left curve is equally valid for systems with small or normal coaxial cable, different lengths and different bit rates, for example for a
- normal coaxial cable $\text{2.6/9.5 mm}$, bit rate $R = 140 \ \rm Mbit/s$, cable length $l = 3 \ \rm km$ ⇒ system $\rm A$,
- small coaxial cable $\text{1.2/4.4 mm mm}$, bit rate $R = 35 \ \rm Mbit/s$, cable length $l = 2.8 \ \rm km$ ⇒ system $\rm B$.
Man erkennt, dass sich selbst bei dieser moderaten Kabeldämpfung $\rm a_∗ = 60 \ \rm dB$ die Impulsantwort aufgrund des Skineffektes $(α_2 = β_2 ≠ 0)$ schon über mehr als $200$ Symboldauern erstreckt. Da das Integral über $h_{\rm K}(t)$ gleich $H_{\rm K}(f = 0) = 1$ ist, wird der Maximalwert sehr klein:
- $${\rm Max}\big [h_{\rm K}(t)\big ] \approx 0.03.$$
In der rechten Grafik sind die Auswirkungen des Phasenparameters $β_1$ zu sehen. Beachten Sie die unterschiedlichen Zeitmaßstäbe der linken und der rechten Skizze:
- Beim System $\rm A$ $(β_1 = 21.78 \ \rm rad/(km · MHz)$, $T = 7.14\ \rm ns)$ führt $β_1$ zu einer Laufzeit von
- $$\tau_{\rm A}= \frac {\beta_1 \cdot l}{2\pi} =\frac {21.78\, { {\rm rad} }/{ {(\rm km \cdot MHz)} }\cdot 3\,{\rm km} }{2\pi} = 10.4\,{\rm \mu s}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\tau_{\rm A}\hspace{0.05cm}' = {\tau_{\rm A} }/{T} \approx 1457\hspace{0.05cm}.$$
- Dagegen erhält man für das System $\rm B$ $(β_1 = 22.18 \ \rm rad/(km · MHz)$, $T = 30 \ \rm ns)$:
- $$\tau_{\rm B}= \frac {\beta_1 \cdot l}{2\pi} =\frac {22.18\, { {\rm rad} }/{ {(\rm km \cdot MHz)} }\cdot 2.8\,{\rm km} }{2\pi} = 9.9\,{\rm µ s}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\tau_{\rm B}\hspace{0.05cm}' ={\tau_{\rm B} }/{T} \approx 330\hspace{0.05cm}.$$
Obwohl hier $τ_{\rm A} ≈ τ_{\rm B}$ gilt, ergeben sich wegen der Zeitnormierung auf $T = 1/R$ völlig unterschiedliche Verhältnisse.
$\text{Fazit:}$ Bei der Simulation und Optimierung von Nachrichtensystemen verzichtet man meist auf den Phasenterm mit $b_1 = β_1 · l$, da dieser ausschließlich eine (oft nicht störende) Laufzeit zur Folge hat, aber keine Signalverzerrung.
Empfangsgrundimpuls
Mit dem Sendegrundimpuls $g_s(t)$ und der Impulsantwort $h_{\rm K}(t)$ ergibt sich für den Empfangsgrundimpuls:
- $$g_r(t) = g_s(t) \star h_{\rm K}(t)\hspace{0.05cm}.$$
Verwendet man am Sender einen NRZ–Rechteckimpuls $g_s(t)$ mit Amplitude $s_0$ und Dauer $Δt_s = T$, so ergibt sich für den Grundimpuls am Ausgang des Koaxialkabels:
- $$g_r(t) = 2 s_0 \cdot \left [ {\rm Q} \left (\frac {{\rm a}_{\rm \star}/\sqrt {\pi}}{ \sqrt{ (t/T - 0.5)}}\right ) - {\rm Q} \left (\frac {{\rm a}_{\rm \star}/\sqrt {\pi}}{ \sqrt{ (t/T + 0.5)}}\right ) \right ]\hspace{0.05cm}.$$
Hierbei bezeichnet $\rm a_∗$ die charakteristische Kabeldämpfung in Neper und ${\rm Q}(x)$ die komplementäre Gaußsche Fehlerfunktion.
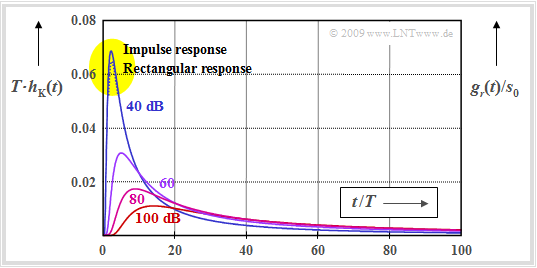
$\text{Beispiel 2:}$ Die Abbildung zeigt für die charakteristischen Kabeldämpfungen $\rm a_∗ = 40 \ \rm dB$, $60 \ \rm dB$, $80 \ \rm dB$ und $100 \ \rm dB$ jeweils
- die normierte Koaxialkabelimpulsantwort $T · h_{\rm K}(t)$ ⇒ Impulsantwort (durchgezogene Kurven), und
- den auf die Sendeamplitude $s_0$ normierten Empfangsgrundimpuls $g_r(t)$ ⇒ Rechteckantwort (gepunktete Linie).
Kleinere Werte von $\rm a_∗$ sind für die Praxis nicht relevant.
Man erkennt aus dieser Darstellung:
- Mit $\rm a_∗ = 40 \ \rm dB$ ist die normierte Rechteckantwort $g_r(t)/s_0$ an der Spitze geringfügig (etwa um den Faktor $0.95)$ kleiner als die normierte Impulsantwort $T · h_{\rm K}(t)$. Hier gibt es eine kleine Differenz zwischen Impulsantwort und Rechteckantwort.
- Dagegen sind für den Fall $a_∗ ≥ 60 \ \rm dB$ die Rechteckantwort und die Impulsantwort innerhalb der Zeichengenauigkeit nicht zu unterscheiden.
- Bei einem RZ–Impuls wäre die obige Gleichung für den Empfangsgrundimpuls noch mit dem Tastverhältnis $Δt_s/T$ zu multiplizieren. In diesem Fall ist $g_r(t)/s_0$ mindestens um diesen Faktor kleiner als $T · h_{\rm K}(t)$.
- Die so modifizierte Gleichung stellt auch eine gute Näherung für andere Sendegrundimpulse dar, so lange $\rm a_∗≥ 60 \ \rm dB$ hinreichend groß ist. $Δt_s$ gibt dann die äquivalente Impulsdauer des Sendegrundimpulses an.
Wir weisen Sie auf das interaktive Applet Zeitverhalten von Kupferkabeln hin, das die hier behandelte Thematik zum Inhalt hat.
Besonderheiten von Koaxialkabelsystemen
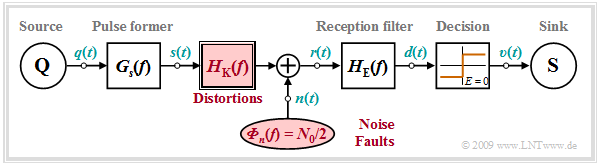
Geht man von binärer Übertragung mit NRZ–Rechteckimpulsen $($Symboldauer $T)$ und einem koaxialen Übertragungskanal aus, so ergibt sich das folgende Systemmodell:
Insbesondere ist zu beachten:
- Bei einer Simulation lässt man zweckmäßigerweise die Laufzeit des Koaxialkabels außer Betracht. Dann gilt für den Empfangsgrundimpuls $g_r(t)$ näherungsweise:
- $$g_r(t) \approx s_0 \cdot T \cdot h_{\rm K}(t) = \frac {s_0 \cdot {\rm a}_{\rm \star}/\pi}{ \sqrt{2 \cdot(t/T)^3}}\cdot {\rm e}^{ -{{\rm a}_{\rm \star}^2}/( {2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}t/T}) } \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} {\rm mit}\hspace{0.15cm}{\rm a}_{\rm \star}\hspace{0.15cm} {\rm in}\hspace{0.15cm} {\rm Neper}\hspace{0.05cm}.$$
- Wegen der guten Abschirmung der Koaxialkabel gegenüber anderen Störungen ist das thermische Rauschen die dominante Störursache. Das Störsignal $n(t)$ ist in diesem Fall gaußverteilt und weiß und wird durch die (zweiseitige) Rauschleistungsdichte $N_0/2$ beschrieben.
- Der weitaus größte Rauschanteil entsteht in der Eingangsstufe des Empfängers, so dass man das Rauschsignal $n(t)$ zweckmäßigerweise an der Schnittstelle "Kabel–Empfänger" addiert. Mit den Amplitudenkoeffizienten $a_{\nu}$ gilt dann für das Empfangssignal:
- $$r(t) = \sum_{\nu = - \infty}^{+ \infty}a_{\nu}\cdot g_r(t - \nu \cdot T)+ n(t) \hspace{0.05cm} .$$
- Dieser Rauschadditionspunkt ist auch deshalb sinnvoll, da durch den Frequenzgang $H_{\rm K}(f)$ alle entlang des Kabels akkumulierten Rauschstörungen entscheidend gedämpft werden.
Aufgaben zum Kapitel
Aufgabe 4.4: Koaxialkabel – Frequenzgang
Aufgabe 4.5: Koaxialkabel – Impulsantwort
Aufgabe 4.5Z: Nochmals Impulsantwort
Quellenverzeichnis
- ↑ Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.