Modulation Methods/Double-Sideband Amplitude Modulation

1. Modulation Methods
2. Amplitude Modulation and Demodulation
3. Double-Sideband Amplitude Modulation

• Previous page
• Next page

• Previous page
• Next page

# OVERVIEW OF SECOND MAIN CHAPTER #

$\Rightarrow \hspace{0.5cm}\text{We are just beginning the English translation of this chapter.}$

After some general explanations of modulation and demodulation, a detailed description of   amplitude modulation  and their associated  demodulators. This chapter deals in detail with:

• the description and realization of double-sideband amplitude modulation (DSB–AM) in the frequency and time domains,
• the characteristics of a synchronous demodulator and the possible applications of an envelope demodulator,
• the similarities/differences of single-sideband modulation compared to DSB-AM and modified AM methods.

Description in the frequency domain

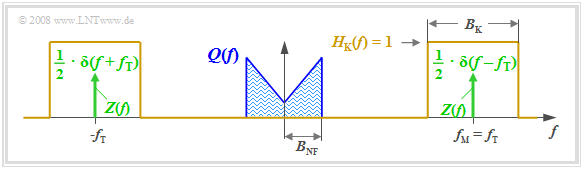
We consider the following problem: a message signal $q(t)$, whose spectrum  $Q(f)$  is bandlimited to the range  $\pm B_{\rm NF}$  (subscript NF from German "Niederfrequenz" ⇒ low frequency), is to be shifted to a higher frequency range where the channel frequency response $H_{\rm K}(f)$ has favorable characteristics, using a harmonic oscillation of frequency  $f_{\rm T}$, which we will refer to as the carrier signal $z(t)$ .

Representation of amplitude modulation in the frequency domain

The diagram illustrates the task, with the following simplifying assumptions:

• The spectrum  $Q(f)$  drawn here is schematic.  It states that only spectral components in the range  $|f| ≤ B_{\rm NF}$  are included in  $q(t)$ . $Q(f)$  could also be a line spectrum.
• Let the channel be ideal in a bandwidth range  $B_{\rm K}$  around frequency  $f_{\rm M}$ , that is, let  $H_{\rm K}(f) = 1$  for  $|f - f_{\rm M}| ≤ B_{\rm K}/2.$  Noise interference is ignored for now.
• Let the carrier signal be cosine   $($phase  $ϕ_T = 0)$  and have amplitude  $A_{\rm T} = 1$  (without a unit).  Let the carrier frequency  $f_{\rm T}$  be equal to the center frequency of the transmission band.
• Thus, the spectrum of the carrier signal  $z(t) = \cos(ω_{\rm T} · t)$  (plotted in green in the graph) is:

$$Z(f) = {1}/{2} \cdot \delta (f + f_{\rm T})+{1}/{2} \cdot \delta (f - f_{\rm T})\hspace{0.05cm}.$$

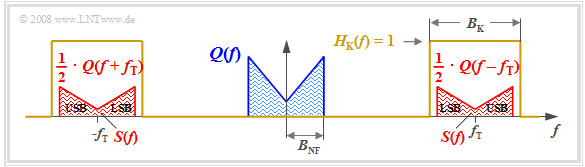
Those familiar with the  laws of spectral transformation  and in particular with the  Convolution Theorem  can immediately give a solution for the spectrum  $S(f)$  of the modulator output signal:

$$S(f)= Z(f) \star Q(f) = 1/2 \cdot \delta (f + f_{\rm T})\star Q(f)+1/2 \cdot \delta (f - f_{\rm T})\star Q(f) = 1/2 \cdot Q (f + f_{\rm T})+ 1/2 \cdot Q(f - f_{\rm T}) \hspace{0.05cm}.$$

$\text{Please note:}$  This equation takes into account that the convolution of a shifted Dirac function  $δ(x – x_0)$  with an arbitrary function $f(x)$  yields the   shifted function  $f(x - x_0)$ .

Spectrum of DSB-AM without a carrier

The diagram displays the result. One can identify the following characteristics:

• Due to the system-theoretic approach with positive and negative frequencies, $S(f)$  is composed of two parts around  $\pm f_{\rm T}$ , each of which have the same shape as  $Q(f)$ .
• The factor  $1/2$  results from the carrier amplitude  $A_{\rm T} = 1$.  Thus,  $s(t = 0) = q(t = 0)$, and the integrals over their spectral functions  $S(f)$  and  $Q(f)$  must also be equal.
• The channel bandwidth  $B_{\rm K}$  must be at least twice the signal bandwidth  $B_{\rm NF}$, which gives the name "double-sideband amplitude modulation"(DSB–AM).
• It should be noted that $B_{\rm NF}$ and $B_{\rm K}$  are absolute and  non-equivalent bandwidths.  The latter are defined over rectangles of equal area and are denoted by $Δf_q$  and  $Δf_{\rm K}$  in our tutorial, respectively.
• The Spectral function  $S(f)$  does not include any Dirac-lines at the carrier frequency  $(\pm f_{\rm T})$.  Therefore, this method is also referred to as "DSB-AM without carrier".
• The frequency components above the carrier frequency  $f_{\rm T}$  are called the upper sideband  (USB), and those below  $f_{\rm T}$  are the lower sideband  (LSB).

Description in the time domain

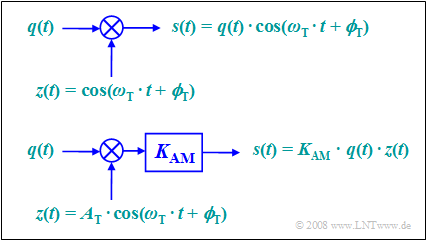
Adapting the notation and nomenclature to this problem, the convolution theorem reads:

$$S(f) = Z(f) \star Q(f)\hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} s(t) = q(t) \cdot z(t) = q(t) \cdot \cos(\omega_{\rm T}\cdot t + \phi_{\rm T})\hspace{0.05cm}.$$

This result is still true if the restrictions made on the last page $($real-valued spectrum  $Q(f)$, carrier phase  $ϕ_{\rm T} = 0)$  are removed. In general, this results in a complex-valued spectral function  $S(f)$.

Models of DSB–AM without a carrier

According to this equation, two models can be given for double-sideband amplitude modulation. These are to be interpreted as follows:

• The first model directly describes the relationship given above, where here the carrier  $z(t) = \cos(ω_{\rm T}t + ϕ_{\rm T})$  is applied without a unit.
• The second model is more in line with the physical conditions, after each signal also has a unit. If  $q(t)$  and  $z(t)$  are voltages respectively, the model still needs to provide a scaling with the modulator constant  $K_{\rm AM}$  (unitso that the output signal  $s(t)$  also represents a voltage waveform.
• If we set  $K_{\rm AM} = 1/A_{\rm T}$, both models are the same.  In the following, we will always assume the simpler model.

Signal waveforms in DSB–AM without a carrier

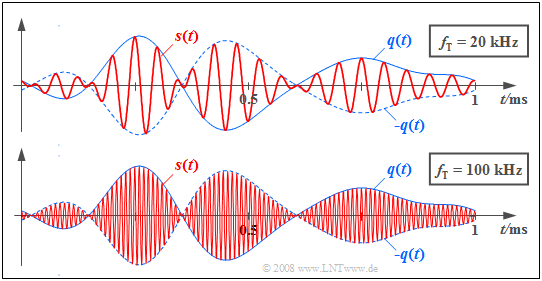
$\text{Example 1:}$  The graph shows in red the transmitted signals  $s(t)$  for DSB–AM with two different carrier frequencies. 

• The source signal  $q(t)$  with bandwidth  $B_{\rm NF} = 4\text{ kHz}$, which is the same in both cases, is drawn in solid blue and the signal  $-q(t)$&nbsp is dashed.
• The carrier signal  $z(t)$  has a cosine shape in both cases.
• In the upper image, the carrier frequency is  $f_{\rm T} = 20\text{ kHz}$  and the lower image  $f_{\rm T} = 100\text{ kHz}$.

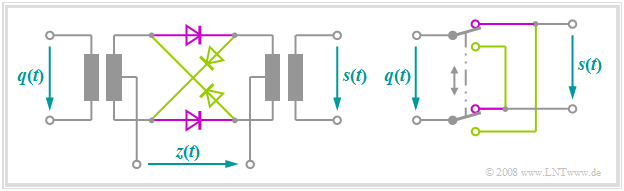
Ring modulator

One possibility to realize "double sideband amplitude modulation with carrier suppression" is offered by a so-called ring modulator, also known as double push-pull diode modulator. Below you can see the circuit on the left and a simple functional diagram on the right.

Ring modulator to realize DSB–AM without a carrier

Without claiming to be complete, the principle can be stated as follows:

• Let the amplitude of the harmonic carrier oscillation  $z(t)$  be much larger than the maximum value $q_{\rm max}$  of the message signal $q(t)$.  Thus, all diodes are operated as switches.
• When the half-wave of the carrier is positive  $(z(t) > 0)$  the two magenta diodes conduct while the light green ones block. Thus, without considering losses, $s(t) = q(t)$ holds.
• For a negative half-wave, the light green diodes conduct and the diodes in the longitudinal branches block. As can be seen from the right image,;$s(t) = \ – q(t)$ holds for this lower switch position.
• Due to the operation of this switch, the harmonic oscillation  $z(t)$  can also be replaced by a periodic square wave signal with identical period duration:

$$z_{\rm R}(t) = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {z(t) >0,} \\ {z(t) <0.} \\ \end{array}$$

• The modulated signal $s(t)$  is then obtained as the product of the message signal  $q(t)$  and this square wave signal  $z_{\rm R}(t)$, whereas in ideal DSB-AM one multiplies by a cosine signal.
• The carrier  $z(t)$  is not itself included in the signal $s(t)$.  Since this is supplied via the center taps of the transformers, the induced voltages cancel out ("DSB-AM without a carrier").

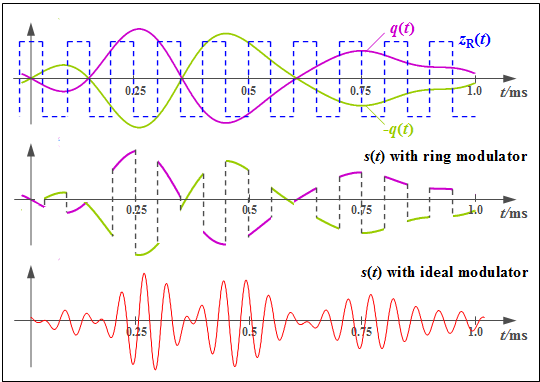
$\text{Example 2:}$  Now we will explain the mode of operation of a ring modulator using typical signal characteristics.  Let the carrier frequency be  $f_{\rm T} = 10\text{ kHz}$.

Signals to illustrate a ring modulator

• The top graph shows the signals  $q(t)$  and  $-q(t)$  as magenta and light green waveforms respectively.

• The bipolar square wave signal $z_{\rm R}(t)$  is shown in blue dashes, and takes the values  $±1$ .

• The middle chart shows the modulated signal from the ring modulator:

$$s_{\rm RM}(t) = q(t) · z_{\rm R}(t).$$

• For comparison, the conventional DSB-AM signal is shown in the bottom graph:

$$s(t) = q(t) · \cos(ω_{\rm T} · t).$$

One can see significant differences, but these can be compensated for in a simple way:

• The Fourier series representation of the periodic square wave signal $z_{\rm R}(t)$  is:

$$z_{\rm R}(t) = \frac{4}{\pi} \cdot \cos(\omega_{\rm T}\cdot t)-\frac{4}{3\pi} \cdot \cos(3\omega_{\rm T}\cdot t) +\frac{4}{5\pi} \cdot \cos(5\omega_{\rm T}\cdot t)- \text{ ...}$$

• The associated spectral function consists of Dirac lines at  $±f_{\rm T}, ±3f_{\rm T}, ±5f_{\rm T}$, etc.  Convolution with  $Q(f)$  leads to the spectral function (the subscript stands for "ring modulator"):

$$S_{\rm RM}(f) = \frac{2}{\pi} \cdot Q (f \pm f_{\rm T})-\frac{2}{3\pi} \cdot Q (f \pm 3f_{\rm T})+\frac{2}{5\pi} \cdot Q (f \pm 5f_{\rm T}) -\text{ ...} \hspace{0.05cm}$$

• From this, it can be seen that by appropriately band-limiting $($for example, to  $±2f_{\rm T})$ and attenuating with  $π/4 ≈ 0.785$  the familiar DSB-AM spectrum can be obtained:

$$S(f) = {1}/{2} \cdot Q (f \pm f_{\rm T})\hspace{0.05cm}.$$

Here it must be taken into account that in the above reasoning,  $B_{\rm NF} \ll f_{\rm T}$  can always be assumed.

AM signals and spectra with a harmonic input signal

Now we will consider a special case, which is important for testing purposes, where not only the carrier signal  $z(t)$ is a harmonic oscillation, but also the message signal to be modulated  $q(t)$ :

$$\begin{align*}q(t) & = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}, \\ \\ z(t) & = \hspace{0.15cm}1 \hspace{0.13cm} \cdot \hspace{0.1cm}\cos(\omega_{\rm T} \cdot t + \phi_{\rm T})\hspace{0.05cm}.\end{align*}$$

Please note:   since we are describing modulation processes, the phase term is used with a plus sign in the above equations.

• Thus,  $ϕ_{\rm N} = - 90^\circ$  represents a sinusoidal input signal  $q(t)$  and  $ϕ_{\rm T} = - 90^\circ$  denotes a sinusoidal carrier signal $z(t)$.
• Therefore, the equation for the modulated signal is:

$$s(t) = q(t) \cdot z(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} t + \phi_{\rm N})\cdot \cos(\omega_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$

This equation can be transformed using the trigonometric addition theorem:

$$s(t) = A_{\rm N}/{2} \cdot \cos \big [(\omega_{\rm T} +\omega_{\rm N})\cdot t + \phi_{\rm T}+ \phi_{\rm N} \big ] + A_{\rm N}/{2} \cdot \cos \big [(\omega_{\rm T} -\omega_{\rm N})\cdot t + \phi_{\rm T}- \phi_{\rm N} \big ]\hspace{0.05cm}.$$

• For cosinusoidal signals  $(ϕ_{\rm T} = ϕ_{\rm N} = 0)$ , this equation simplifies to

$$s(t) = {A_{\rm N}}/{2} \cdot \cos\big[(\omega_{\rm T}+\omega_{\rm N})\cdot t\big] + {A_{\rm N}}/{2} \cdot \cos\big[(\omega_{\rm T} -\omega_{\rm N})\cdot t \big]\hspace{0.05cm}.$$

• Using a Fourier transform we arrive at the spectral function:

$$S(f) = {A_{\rm N}}/{4} \cdot \big[\delta ( f - f_{\rm T} - f_{\rm N})+\delta ( f + f_{\rm T} + f_{\rm N})\big)] + {A_{\rm N}}/{4} \cdot \big[ \delta ( f - f_{\rm T}+ f_{\rm N})+\delta ( f+ f_{\rm T} - f_{\rm N} ) \big]\hspace{0.05cm}.$$

This result, which would also have been arrived at via convolution, states:

• The spectrum consists of four Dirac lines at frequencies  $±(f_{\rm T} + f_{\rm N})$  and  $±(f_{\rm T} - f_{\rm N})$, where in both bracket expressions the first Dirac function indicates the one for positive frequencies.
• The weights of all Dirac functions are equal and each is  $A_{\rm N}/4$.  The sum of these weights - that is, the integral over $S(f)$ – is equal to the signal value  $s(t = 0) = A_{\rm N}$.
• The Dirac lines remain for  $ϕ_{\rm T} ≠ 0$  and/or  $ϕ_{\rm N} ≠ 0$  at the same frequencies.  However, complex rotation factors must then be added to the weights  $A_{\rm N}/4$ .

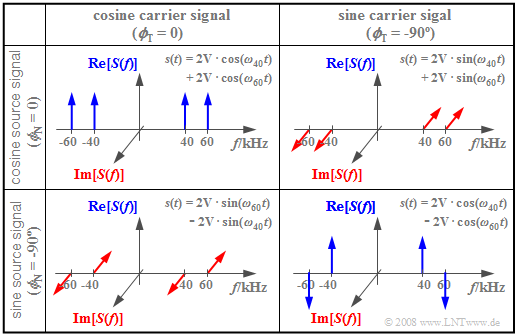
$\text{Example 3:}$  The following diagram shows the spectral functions  $S(f)$  for different values of  $ϕ_{\rm T}$  and  $ϕ_{\rm N}$, respectively.  The other parameters are assumed to be  $f_{\rm T} = 50\text{ kHz}$,  $f_{\rm N} = 10\text{ kHz}$  and  $A_{\rm N} = 4\text{ V}$ . Thus, the magnitudes of all Dirac lines are $A_{\rm N}/4 = 1\text{ V}$.

Typical spectra for DSB-AM

• The upper left image shows the case just discussed: both the carrier and the message signal are cosine. Thus, the amplitude modulated signal  $s(t)$  s composed of two cosine oscillations with  $ω_{60} = 2 π · 60\text{ kHz}$  and  $ω_{40} = 2 π · 40\text{ kHz}$ .

• For the other three constellations, at least one of the signals  $q(t)$  or  $z(t)$  sinusförmig, is sinusoidal, so that  $s(0) = 0$  always holds.  Thus, for these spectra, the sum of the four impulse weights each add up to zero.

• The bottom right image depicts  $s(t) = A_{\rm N} · \sin(ω_{\rm N} t) · \sin(ω_{\rm T}t)$.  Multiplying two odd functions yields the even function  $s(t)$  and thus a real spectrum  $S(f)$.  In contrast, the other two constellations each result in imaginary spectral functions.

Double-Sideband Amplitude Modulation with carrier

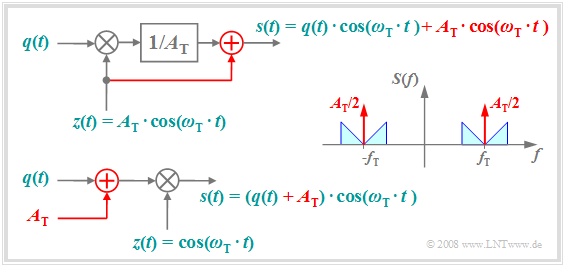
The following diagram shows how to get from "DSB-AM without a carrier" to the better known variant "DSB-AM with carrier". This has the advantage that the demodulator can be realized much more easily and cheaply by a simple manipulation at the transmitter.

Models of DSB–AM with carrier

The diagram is to be interpreted as follows:

• The top plot shows the physical model of the "DSB-AM with carrier", with changes from the "DSB-AM without a carrier" highlighted in red.
• The carrier signal  $z(t) = A_{\rm T} · \cos(ω_{\rm T} · t)$  is added to the signal  $s(t)$  , which causes two additional Dirac functions in the spectrum  $±f_{\rm T}$  bewirkt,  ach with impulse weight  $A_{\rm T}/2$.
• Adding the DC signal  $A_{\rm T}$  to the source signal and then multiplying by the dimensionless carrier  $z(t)$  as shown in the lower sketch results in the same signal  $s(t)$  and spectrum  $S(f)$  as above.
• Thus, the second representation is equivalent to the upper model. In both cases the carrier phase is only set to  $ϕ_{\rm T} = 0$  for the sake of simplified presentation.

$\text{Beispiel 4:}$  Die  Zweiseitenband-Amplitudenmodulation mit Träger  findet auch heutzutage noch ihre Hauptanwendung in der Rundfunkübertragung auf

• Langwelle    $($Frequenzbereich  $\text{30 kHz}$ ... $\text{300 kHz})$,
• Mittelwelle  $($Frequenzbereich  $\text{300 kHz}$ ... $\text{3 MHz})$,
• Kurzwelle    $($Frequenzbereich  $\text{3 MHz}$ ... $\text{30 MHz})$.

Diese Frequenzen werden jedoch mehr und mehr für digitale Anwendungen freigegeben, zum Beispiel für  Digital Video Broadcast  (DVB).

Eine Anwendung von  Zweiseitenband-Amplitudenmodulation ohne Träger  gibt es beispielsweise beim UKW-Stereo-Rundfunk:

• Hier wird das Differenzsignal zwischen den beiden Stereokanälen bei  $\text{39 kHz}$  trägerlos amplitudenmoduliert.
• Dann werden das Summensignal der beiden Kanäle  $($jeweils im Bereich  $\text{30 Hz}$ ... $\text{15 kHz})$, ein Hilfsträger bei  $\text{19 kHz}$  sowie das Differenzsignal zusammengefasst und frequenzmoduliert.

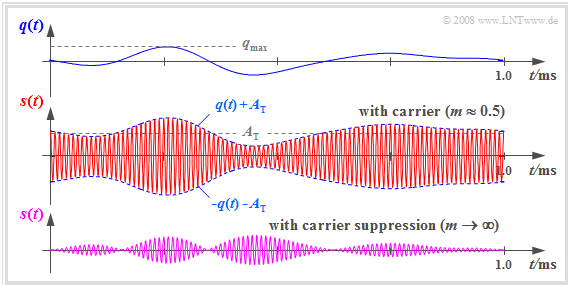
$\text{Beispiel 5:}$  Die folgenden Signalverläufe sollen das Prinzip der „ZSB–AM mit Träger” weiter verdeutlichen.

Signalverläufe bei der ZSB–AM mit Träger

• Oben sehen Sie einen Ausschnitt des auf Frequenzen  $\vert f \vert \le 4\text{ kHz}$  begrenzten Quellensignal  $q(t)$.

• $s(t)$  ergibt sich, wenn man zu  $q(t)$  den Gleichanteil  $A_{\rm T}$  addiert und die Signalsumme mit dem Trägersignal  $z(t)$  der Frequenz  $f_{\rm T} = 100\text{ kHz}$  multipliziert.

• Unten ist zum Vergleich das Sendesignal der „ZSB–AM ohne Träger” dargestellt.

Ein Vergleich dieser Signalverläufe zeigt:

• Durch die Zusetzung des Gleichanteils  $A_{\rm T}$  wurde erreicht, dass nun das Nachrichtensignal  $q(t)$  in der Hüllkurve von  $s(t)$  zu erkennen ist.
• Dadurch kann die  Hüllkurvendemodulation  angewandt werden, die einfacher und billiger zu realisieren ist als die kohärente  Synchrondemodulation.
• Voraussetzung für die Anwendung des Hüllkurvendemodulators ist aber ein Modulationsgrad  $m <1$.  Dieser ist wie folgt definiert:

$$m = \frac{q_{\rm max} }{A_{\rm T} } \hspace{0.3cm}{\rm mit}\hspace{0.3cm} q_{\rm max} = \max_{t} \hspace{0.05cm} \vert q(t) \vert\hspace{0.05cm}.$$

• Der Vorteil eines einfacheren Demodulators muss aber durch eine deutlich höhere Sendeleistung erkauft werden, da der Leistungsbeitrag des Trägers nicht zur Demodulation genutzt werden kann.
• Weiter ist zu darauf zu achten, dass das Quellensignal keinen Gleichanteil beinhaltet, da dieser durch den Träger überdeckt würde.  Bei Sprach– und Musiksignalen ist dies allerdings keine große Einschränkung.

Beschreibung der ZSB-AM durch das analytische Signal

Spektrum des analytischen Signals in zwei verschiedenen Darstellungsformen

Im weiteren Verlauf wird zur Vereinfachung von Grafiken meist das Spektrum  $S_+(f)$  des  analytischen Signals  anstelle des tatsächlichen, physikalischen Spektrums  $S(f)$  angegeben. 

Beispielhaft betrachten wir hier eine  „ZSB–AM mit Träger”  und folgende Signale:

$$\begin{align*}s(t) & = \left(q(t) + A_{\rm T}\right) \cdot \cos(\omega_{\rm T}\cdot t + \phi_{\rm T})\hspace{0.05cm}, \\ \\ q(t) & = A_{\rm N} \cdot \cos(\omega_{\rm N}\cdot t + \phi_{\rm N})\hspace{0.05cm}.\end{align*}$$

Dann lautet das dazugehörige analytische Signal:

$$s_+(t) = A_{\rm T} \cdot {\rm e}^{{\rm j}\hspace{0.03cm} \cdot \hspace{0.01cm}(\omega_{\rm T}\cdot \hspace{0.02cm}t \hspace{0.05cm}+ \hspace{0.05cm}\phi_{\rm T})}+ \frac{A_{\rm N}}{2} \cdot {\rm e}^{{\rm j}\hspace{0.03cm} \cdot \hspace{0.01cm}((\omega_{\rm T} \hspace{0.05cm}+ \hspace{0.05cm} \omega_{\rm N} )\hspace{0.02cm}\cdot \hspace{0.02cm}t \hspace{0.05cm}+ \hspace{0.05cm} \phi_{\rm T}+ \phi_{\rm N})} + \frac{A_{\rm N}}{2} \cdot {\rm e}^{{\rm j}\hspace{0.03cm} \cdot \hspace{0.01cm}((\omega_{\rm T} \hspace{0.05cm}- \hspace{0.05cm} \omega_{\rm N} )\hspace{0.02cm}\cdot \hspace{0.02cm}t \hspace{0.05cm}+ \hspace{0.05cm} \phi_{\rm T}- \phi_{\rm N})} \hspace{0.05cm}.$$

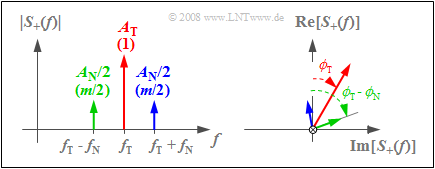
Die zugehörige Spektralfunktion  $S_+(f)$  besteht aus drei Diraclinien mit jeweils komplexen Gewichten entsprechend der Grafik:

• Die linke Skizze zeigt den Betrag  $|S_+(f)|$, wobei  $A_{\rm T}$  das Gewicht des Trägers angibt und  $A_{\rm N}/2$  die Gewichte von  OSB  (oberes Seitenband)  und  USB  (unteres Seitenband).
• In Klammern stehen die auf  $A_{\rm T}$  normierten Werte.  Da hier  $q_{\rm max} = A_{\rm N}$  gilt, erhält man mit dem Modulationsgrad  $m = A_{\rm N}/A_{\rm T}$  als normierte Gewichte von oberem und unterem Seitenband jeweils  $m/2$.
• Die rechte Skizze gibt einen Blick in Richtung der Frequenzachse und zeigt die Phasenwinkel von Träger  $(ϕ_{\rm T})$, USB  $(ϕ_{\rm T} – ϕ_{\rm N})$  und OSB  $(ϕ_{\rm T} + ϕ_{\rm N})$.

Amplitudenmodulation durch quadratische Kennlinie

Nichtlinearitäten sind in der Nachrichtentechnik meist unerwünscht und störend.  Wie im Kapitel  Nichtlineare Verzerrungen  des Buches „Lineare zeitinvariante Systeme” dargelegt, führen sie dazu, dass

• das Superpositionsprinzip nicht mehr anwendbar ist,
• das Übertragungsverhalten von der Größe des Eingangssignals abhängt,  und
• die Verzerrungen von nichtlinearer Art und damit irreversibel sind.

Eine Nichtlinearität der allgemeinen Form

$$y(t) = c_0 + c_1 \cdot x(t) + c_2 \cdot x^2(t)+ c_3 \cdot x^3(t) + \text{...}$$

kann aber auch zur Realisierung einer ZSB–AM genutzt werden.  Unter der Voraussetzung, dass

• nur die Koeffizienten  $c_1$  und  $c_2$  vorhanden sind, und
• das Eingangssignal  $x(t) = q(t) + z(t)$  angelegt wird,

erhält man für das Ausgangssignal der Nichtlinearität:

$$y(t) = c_1 \cdot q(t) + c_1 \cdot z(t) + c_2 \cdot q^2(t)+ 2 \cdot c_2 \cdot q(t)\cdot z(t)+ c_2 \cdot z^2(t)\hspace{0.05cm}.$$

Der erste, der dritte und der letzte Anteil liegen – spektral gesehen – bei  $| f | ≤ 2 · B_{\rm NF}$  bzw.  $| f | = 2 · f_{\rm T}$.

Entfernt man diese Signalanteile durch einen Bandpass und berücksichtigt  $z(t) = A_{\rm T} · \cos(ω_{\rm T} · t)$, so erhält man die für  „ZSB–AM mit Träger”  typische Gleichung 
(nur noch der zweite und der vierte Term):

$$s(t) = c_1 \cdot A_{\rm T} \cdot \cos(\omega_{\rm T} \cdot t ) + 2 \cdot c_2 \cdot A_{\rm T} \cdot q(t)\cdot \cos(\omega_{\rm T} \cdot t )\hspace{0.05cm}.$$

Der Modulationsgrad ist bei dieser Realisierungsform durch die Koeffiziente  $c_1$  und  $c_2$  veränderbar:

$$m = \frac{2 \cdot c_2 \cdot q_{\rm max}}{c_1} \hspace{0.05cm}.$$

Eine Diode und der Feldeffekttransistor besitzen mit guter Näherung eine solche quadratische Kennlinie und können zur Realisierung einer ZSB–AM genutzt werden.  Kubische Anteile  $(c_3 ≠ 0)$  und Nichtlinearitäten höherer Ordnung führen allerdings zu (großen) nichtlinearen Verzerrungen.

Aufgaben zum Kapitel

Aufgabe 2.1: ZSB-AM mit Cosinus? Oder mit Sinus?

Aufgabe 2.1Z: ZSB-AM ohne/mit Träger

Aufgabe 2.2: Modulationsgrad

Aufgabe 2.2Z: Leistungsbetrachtung

Aufgabe 2.3: ZSB–AM–Realisierung

Aufgabe 2.3Z: ZSB durch Nichtlinearität