Theory of Stochastic Signals/Markov Chains

1. Theory of Stochastic Signals
2. Probability Calculation
3. Markov Chains

• Previous page
• Next page

• Previous page
• Next page

Considered scenario

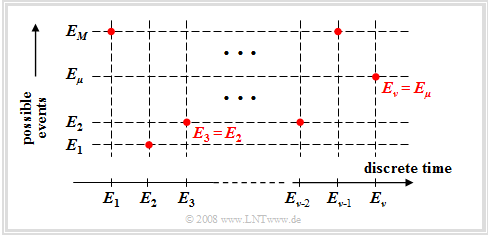
WFinally, we consider the case where one runs a random experiment continuously and that at each discrete time  $(ν = 1, 2, 3, \text{...})$  a new event  $E_ν$ . Here, let hold:

Possible events and event sequence

$$E_\nu \in G = \{ E_{\rm 1}, E_{\rm 2}, \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_\mu , \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_M \}.$$

This mathematically not quite proper nomenclature means (see graph):

• The  $M$  possible events are numbered consecutively with the index  $μ$ .
• The index  $ν$  names the discrete time points at which events occur.

For simplicity, we restrict ourselves in the following to the case  $M = 2$  with the universal set  $G = \{ A, \ B \}$.  Let further hold:

• The probability of event  $E_ν$  may well depend on all previous events – that is, on events  $E_{ν\hspace{0.05cm}-1},  E_{ν\hspace{0.05cm}-2},  E_{ν\hspace{0.05cm}-3},$ , and so on.
• This statement also means that in this chapter we consider a  sequence of events with internal statistical ties .

This scenario is a special case of a discrete-time, discrete-value random process, which will be discussed in more detail in the chapter } Random Processes  to be discussed in more detail.

$\text{Example 1:}$  Cards are drawn one after the other from a deck of  $32$  cards (including four aces). With the events

• $A\text{ :}=$  „the drawn card is an ace”, and
• $B = \overline{A}:=$  „the drawn card is not an ace”, the probabilities at time  $ν = 1$:

$${\rm Pr} (A_{\rm 1}) ={4}/{32}= {1}/{8}, \hspace{0.5cm}{\rm Pr} (B_{\rm 1}) = {28}/{32}= {7}/{8}.$$

The probability  ${\rm Pr} (A_{\rm 2})$,  that an ace is drawn as the second card  $(ν = 2)$  now depends on,

• whether an ace was drawn at time  $ν = 1$   ⇒   ${\rm Pr} (A_{\rm 2}) = 3/31 < 1/8$,  or
• whether at time  $ν = 1$  no ace was drawn   ⇒   ${\rm Pr} (A_{\rm 2}) = 4/31 > 1/8$.

Also, the probabilities  ${\rm Pr} (A_{\nu})$  at later times  $ν$  always depend on the occurrence or non-occurrence of all previous events  $E_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} ,E_{ν\hspace{0.05cm}–1}$ .

General definition of a Markov chain

In special cases, which however occur very frequently, the scenario described above can be described by a Markov chain.

$\text{Definition:}$  A  $k$-th orderMarkov Chain  serves as a model for time- and value-discrete processes, where

1.  the event probabilities at time  $ν$  depend on the previous events   $E_{ν\hspace{0.05cm}–1}, \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_{ν\hspace{0.05cm}–k}$  abhängen, and
2.   can be expressed by  $M^{k+1}$  conditional probabilities.

Second order Markov chain

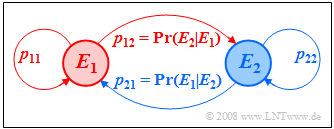
The diagram illustrates this issue using  $k = 2$ as an example..

Therefore, for  $M = 2$  there are  $2^{k+1}$  such conditional probabilities. 

$${\rm Pr} ( E_\nu \hspace {0.05cm}\vert \hspace {0.05cm}E_{\nu {\rm -1 } },\hspace {0.1cm}\text{...}\hspace {0.1cm}, E_{\nu { -k } }).$$

With  $E_{\nu }\in \{ A, B \}, \hspace {0.1cm}\text{...}\hspace {0.1cm}, E_{\nu { -k } } \in \{ A, B \}$  these are:

• ${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } }, A_{\nu { -2 } })$,  ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } }, A_{\nu { -2 } })$,  
• ${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } },B_{\nu { -2 } })$,  ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}A_{\nu {\rm -1 } }, B_{\nu { -2 } })$,  
• ${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, A_{\nu { -2 } })$,  ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, A_{\nu { -2 } })$,  
• ${\rm Pr} ( A_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, B_{\nu { -2 } })$,  ${\rm Pr} ( B_\nu \hspace {0.05cm}\vert \hspace {0.05cm}B_{\nu {\rm -1 } }, B_{\nu { -2 } })$.

$\text{Example 2:}$  Natural languages are often describable by Markov chains, although the order  $k$  tends to infinity.  In this example, however, texts are only approximated by second-order Markov chains.

Synthetically generated texts (German and English)

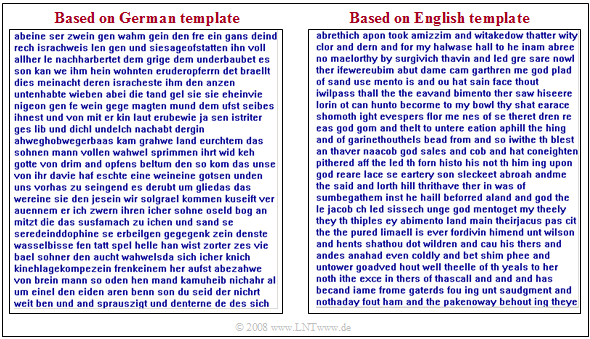
The graphic shows two synthetically generated texts:

• The left text was synthetically generated starting from a German book template with bindings up to second order.
• For the right text, an English template was used.

One recognizes despite the restriction to  $k = 2$  many (short) German and/or English words and also that German words are on the average longer than English.  There is no meaningful content, but the structure of the respective language is recognizable.

First order Markov chain

In the following, we always restrict ourselves to the special case  $k =1$ .

$\text{Definition:}$  In a  First Order Markov Chain  only the statistical binding to the last event is considered, which in practice is usually the strongest.

A binary first order Markov chain   ⇒   universal set  $G = \{ A, \ B \}$  has the following event probabilities at time  $\nu$ :

$${\rm Pr}(A_\nu) = {\rm Pr}(A_\nu \hspace{0.05cm} \vert \hspace{0.05cm}A_{\nu - 1}) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) \cdot {\rm Pr}(B_{\nu - 1}) ,$$

$${\rm Pr}(B_\nu) = {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}A_{\nu - 1}) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) \cdot {\rm Pr}(B_{\nu - 1}) .$$

Regarding these equations, we note:

• ${\rm Pr}(A_\nu)$  sis shorthand for the probability that at timenbsp; $ν$  the event   $E_ν = A = \overline{B}$  occurs, and  ${\rm Pr}(B_\nu) = 1 - {\rm Pr}(A_\nu)$ holds.
• At each time there are four transition probabilities  ${\rm Pr}(E_ν\hspace{0.05cm} |\hspace{0.05cm} E_{ν–1})$, but only two of them are independent, because it holds:

$${\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}) = 1 - {\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}), \hspace{0.5cm}{\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}) = 1 - {\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}).$$

• Generalizing this last statement, one arrives at the result that for a Markov chain with  $M$ events,  there are exactly  $M · (M – 1)$  independent transition probabilities at each time  $ν$ .

$\text{Example 3:}$  With the given transition probabilities

$${\rm Pr}(A_ν\hspace{0.05cm}\vert\hspace{0.05cm} A_{ν–1}) = 0.2 \hspace{0.3cm}\text{und}\hspace{0.3cm} {\rm Pr}(B_ν\hspace{0.05cm} \vert\hspace{0.05cm} B_{ν–1}) = 0.4$$

the other two transition probabilities are also uniquely specified

$${\rm Pr}(B_ν\hspace{0.05cm} \vert\hspace{0.05cm} A_{ν–1}) = 1- 0.2 = 0.8 \hspace{0.3cm}\text{und}\hspace{0.3cm} {\rm Pr}(A_ν\hspace{0.05cm} \vert\hspace{0.05cm} B_{ν–1}) = 1- 0.4 = 0.6.$$

Homogeneous Markov chains

Applicability of Markov chains to practical problems is usually only given further restrictive conditions.

$\text{Definition:}$  If all transition probabilities are independent of the time  $ν$, the Markov chain is  homogeneous .

In the case  $M = 2$  we use the following abbreviations for this:

$${\rm Pr}(A \hspace{0.05cm} \vert \hspace{0.05cm}A) = {\rm Pr}(A_\nu \hspace{0.05cm}\vert \hspace{0.05cm}A_{\nu - 1}) , \hspace{0.5cm} {\rm Pr}(A \hspace{0.05cm} \vert\hspace{0.05cm}B) = {\rm Pr}(A_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) ,$$

$${\rm Pr}(B \hspace{0.05cm} \vert\hspace{0.05cm}A) = {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}A_{\nu - 1}) , \hspace{0.5cm} {\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm}B) = {\rm Pr}(B_\nu \hspace{0.05cm} \vert \hspace{0.05cm}B_{\nu - 1}) .$$

Thus, the event probabilities of a binary homogeneous Markov chain, which are absolute probabilities in contrast to the conditional transition probabilities, are :

First order homogeneous Markov chain

$${\rm Pr}(A_\nu) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B_{\nu - 1}) ,$$

$${\rm Pr}(B_\nu) = {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B_{\nu - 1}) .$$

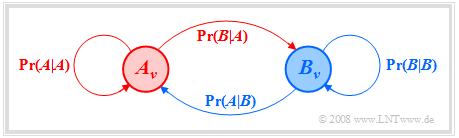
We can also read from the Markov diagram:

• The sum of the  outgoing arrows  of an event is always one

$${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) =1,$$

$${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) =1.$$

• The sums  ${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) + {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B)$  bzw.  ${\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B)$ , on the other hand, are not subject to any restrictions.

You can calculate and display the "transient behavior" of the event probabilities of such a binary Markov chain with the interactive applet (German)   Event Probabilities of a First Order Markov Chain. .

Stationäre Wahrscheinlichkeiten

Wichtige Eigenschaften von Zufallsprozessen sind  Stationarität  und  Ergodizität.  Obwohl diese Begriffe erst im vierten Hauptkapitel  "Zufallsgrößen mit statistischen Bindungen"  definiert werden, wenden wir sie hier bereits vorausgreifend auf Markovketten an.

$\text{Definition:}$  Sind bei einer Markovkette neben den Übergangswahrscheinlichkeiten auch alle Ereigniswahrscheinlichkeiten unabhängig von der Zeit  $ν$, so bezeichnet man die Markovkette als  stationär  (englisch:  stationary).  Man verzichtet dann auf den Index $ν$ und schreibt im binären Fall:

$${\rm Pr}(A_\nu ) = {\rm Pr}(A ) \hspace{0.5 cm} {\rm bzw.} \hspace{0.5 cm} {\rm Pr}(B_\nu ) = {\rm Pr}(B).$$

Diese Größen nennt man auch die  ergodischen Wahrscheinlichkeiten  der Markovkette.

Stationäre Markovketten weisen die nachfolgend genannten Besonderheiten auf:

• Zur Berechnung der ergodischen Wahrscheinlichkeiten einer binären Markovkette  $(M =2)$  kann man folgende Gleichungen verwenden:

$${\rm Pr}(A) = {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B) ,$$

$${\rm Pr}(B) = {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) \cdot {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}B) \cdot {\rm Pr}(B) .$$

• Da diese Gleichungen linear voneinander abhängen, darf man nur eine hiervon benutzen.  Als zweite Bestimmungsgleichung kann man beispielsweise verwenden:

$${\rm Pr}(A) + {\rm Pr}(B) = 1.$$

• Die ergodischen Wahrscheinlichkeiten ergeben sich daraus zu

$${\rm Pr}(A) = \frac {{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) }{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) }\hspace{0.1cm}, \hspace{0.5cm}{\rm Pr}(B) = \frac {{\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) }{{\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm}B) + {\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm}A) }.$$

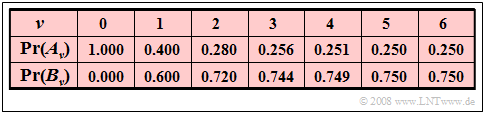
$\text{Beispiel 4:}$  Wir betrachten eine binäre Markovkette mit den Ereignissen  $A$  und $B$  und den Übergangswahrscheinlichkeiten  ${\rm Pr}(A \hspace{0.05cm} \vert\hspace{0.05cm}A) = 0.4$  und  ${\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm}B) = 0.8$.
Weiterhin setzen wir voraus, dass jede Realisierung dieser Kette zum Startzeitpunkt  $ν = 0$  mit dem Ereignis  $A$  beginnt.

Man erhält dann die nachfolgend aufgelisteten Ereigniswahrscheinlichkeiten (mit drei Nachkommastellen):

Zum Einschwingen der Ereigniswahrscheinlichkeiten

Es handelt sich hier im strengen Sinne um eine nichtstationäre Markovkette, die jedoch schon nach kurzer Zeit (nahezu) eingeschwungen ist:

• Zu späteren Zeiten  $(ν > 5)$  werden die Ereigniswahrscheinlichkeiten  ${\rm Pr}(A_ν) \approx 1/4$  und  ${\rm Pr}(B_ν) \approx 3/4$  nicht mehr gravierend verändert.
• Aus der Angabe  ${\rm Pr}(A_{ν=5}) = 0.250$  und  ${\rm Pr}(B_{ν=5}) = 0.750$  sollte allerdings nicht geschlossen werden, dass die Markovkette zum Zeitpunkt  $ν = 5$  schon vollkommen eingeschwungen ist.
• Die exakten Werte sind nämlich  ${\rm Pr}(A_{ν=5}) = 0.25024$  und  ${\rm Pr}(B_{ν=5}) = 0.74976$.

$\text{Fazit:}$  Bei einer stationären Markovkette treten sehr lange nach Einschalten der Kette  $(ν → ∞)$  mit guter Näherung stets die ergodischen Wahrscheinlichkeiten auf, unabhängig von den Startbedingungen  ${\rm Pr}(A_0)$  und  ${\rm Pr}(B_0) = 1 - {\rm Pr}(A_0)$.

Matrix-Vektordarstellung

Homogene Markovketten können mit Vektoren und Matrizen sehr kompakt dargestellt werden. Dies empfiehlt sich insbesondere bei mehr als zwei Ereignissen:

$$E_\nu \in G = \{ E_{\rm 1}, E_{\rm 2}, \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_\mu , \hspace{0.1cm}\text{...}\hspace{0.1cm}, E_M \}.$$

Für die Matrix-Vektorendarstellung verwenden wir folgende Nomenklatur:

• Die  $M$  Wahrscheinlichkeiten zum Zeitpunkt  $ν$  fassen wir in einem Spaltenvektor zusammen:

$${\mathbf{p}^{(\nu)}} = \left[ \begin{array}{c} {p_{\rm 1}}^{(\nu)} \\ \dots \\ {p_{M}}^{(\nu)} \end{array} \right] \hspace{0.5cm}{\rm mit} \hspace{0.5cm} {p_{\mu}}^{(\nu)} = {\rm Pr}(E_\nu = E_\mu ).$$

• Die Übergangswahrscheinlichkeiten werden durch eine  $M \times M$-Matrix ausgedrückt:

$${\mathbf{P}} =\left( p_{ij} \right) = \left[ \begin{array}{cccc} p_{11} & p_{12} & \cdots & p_{1M} \\ p_{21} & p_{22}& \cdots & p_{2M} \\ \dots & \dots & \dots & \dots \\ p_{M1} & p_{M2} & \cdots & p_{MM} \end{array} \right] \hspace{0.5cm}{\rm mit} \hspace{0.5cm} {p_{ij}} = {\rm Pr}(E_{\nu +1 } = E_j \hspace{0.05cm}| \hspace{0.05cm} E_{\nu } = E_i).$$

Die nebenstehende Abbildung verdeutlicht diese Nomenklatur am Beispiel  $M = 2$.  Der neue Ereigniswahrscheinlichkeitsvektor nach einem Schritt lautet:

Zur Bezeichnung der Übergangswahrscheinlichkeiten

$${\mathbf{p}^{(\nu + 1)}} = {\mathbf{P}}^{\rm T} \cdot {\mathbf{p}^{(\nu )}} .$$

${\mathbf{P}^{\rm T}}$  bezeichnet hierbei die  transponierte  Matrix zu  $\mathbf{P}$.  Nach  $n$  Schritten ergibt sich somit

$${\mathbf{p}^{(\nu +{\it n})}} = \left( {\mathbf{P}}^{\rm T} \right)^n \cdot {\mathbf{p}^{(\nu )}} .$$

Im Grenzübergang  $(n → ∞)$  erreicht man dann stets die Stationarität der Markovkette:

$$\lim_{n \to\infty}\hspace{0.1cm}{\mathbf{p}^{(\nu + n)}} = \lim_{n \to\infty} \left( {\mathbf{P}}^{\rm T} \right)^n \cdot {\mathbf{p}^{(\nu )}} = {\mathbf{p}}_{\rm erg}= \left[ \begin{array}{c} {p_{\rm 1}} \\ \dots \\ {p_{M}} \end{array} \right] .$$

$\text{Definition:}$  Multipliziert man die Übergangsmatrix  ${\mathbf{P} }$  unendlich oft mit sich selbst und benennt das Ergebnis mit  ${\mathbf{P} }_{\rm erg}$, so besteht die resultierende Matrix aus  $M$  gleichen Zeilen:

$${\mathbf{P} }_{\rm erg} = \lim_{n \to\infty} {\mathbf{P} }^n = \left[ \begin{array}{cccc} p_{1} & p_{2} & \cdots & p_{M} \\ p_{1} & p_{2}& \cdots & p_{M} \\ \dots & \dots & \dots & \dots \\ p_{1} & p_{2} & \cdots & p_{M} \end{array} \right] .$$

Die Wahrscheinlichkeiten  $p_1, \hspace{0.1cm}\text{...}\hspace{0.1cm}, p_M$  in jeder dieser Zeilen bezeichnet man als die  ergodischen Wahrscheinlichkeiten.

Markovdiagramm mit drei Ereignissen

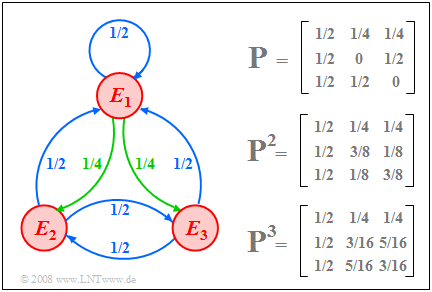
$\text{Beispiel 5:}$  Wir betrachten beispelhaft eine Markovkette mit den Ereignissen  $E_1,  E_2$  und  $E_3$   ⇒   $M=3$. Die Grafik zeigt

• links das Markovdiagramm,
• rechts oben die Übergangsmatrix  $\mathbf{P}$ und
• darunter deren Potenzen  $\mathbf{P}^2$  und  $\mathbf{P}^3$.

Im Markovdiagramm sind alle Übergangswahrscheinlichkeiten mit dem Zahlenwert  $1/2$  blau eingezeichnet;  grün kennzeichnet die Wahrscheinlichkeit  $1/4$.

• Beim Start  $(ν =0)$  seien alle Ereignisse gleichwahrscheinlich.  Für  $ν = 1$  gilt dann:

$${\mathbf{p}^{(1)} } = {\mathbf{P} }^{\rm T} \cdot {\mathbf{p}^{(0 )} }= \left[ \begin{array}{ccc} 1/2 & 1/2& 1/2 \\ 1/4 & 0 & 1/2 \\ 1/4& 1/2& 0 \end{array} \right] \left[ \begin{array}{c} 1/3 \\ 1/3 \\ 1/3 \end{array} \right] = \left[ \begin{array}{c} 1/2 \\ 1/4 \\ 1/4 \end{array} \right] .$$

Hieraus ist zu ersehen, dass man von der Matrix  $\mathbf{P}$  durch den Austausch der Zeilen und Spalten zur transponierten Matrix  ${\mathbf{P}^{\rm T} }$  kommt.

• Zum Zeitpunkt  $ν =2$  (und auch zu allen späteren Zeiten) ergeben sich die gleichen Wahrscheinlichkeiten:

$${\mathbf{p}^{(2)} } = {\mathbf{P} }^{\rm T} \cdot {\mathbf{p}^{(1 )} }= \left[ \begin{array}{ccc} 1/2 & 1/2& 1/2 \\ 1/4 & 0 & 1/2 \\ 1/4& 1/2& 0 \end{array} \right] \left[ \begin{array}{c} 1/2 \\ 1/4 \\ 1/4 \end{array} \right] = \left[ \begin{array}{c} 1/2 \\ 1/4 \\ 1/4 \end{array} \right] .$$

Das bedeutet:  Die ergodischen Wahrscheinlichkeiten der drei Ereignisse sind  $1/2$  $($für  $E_1)$,  $1/4$  $($für  $E_2)$,  und $1/4$  $($für  $E_3)$.

• Dieses Ergebnis hätte man auch direkt aus der ergodischen Matrix ablesen können:

$${\mathbf{P} }_{\rm erg} = \lim_{n \to\infty} {\mathbf{P} }^n = \left[ \begin{array}{ccc} 1/2 & 1/4 & 1/4 \\ 1/2 & 1/4 & 1/4 \\ 1/2 & 1/4 & 1/4 \end{array} \right] .$$

Diese ergibt sich durch fortlaufende Multiplikation der Übergangsmatrix mit sich selbst.

• Im obigen Bild sind die Potenzen  $\mathbf{P}^2$  und  $\mathbf{P}^3$  angegeben, die sich der Matrix  $\mathbf{P}_{\rm erg}$  annähern.

Aufgaben zum Kapitel

Aufgabe 1.6: Übergangswahrscheinlichkeiten

Aufgabe 1.6Z: Ergodische Wahrscheinlichkeiten

Aufgabe 1.7: Ternäre Markovkette

Aufgabe 1.7Z: BARBARA-Generator