Difference between revisions of "Theory of Stochastic Signals/Poisson Distribution"
| Line 8: | Line 8: | ||
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ The '''Poisson distribution''' is a limiting case of the [[Theory_of_Stochastic_Signals/Binomial_Distribution#General_description_of_the_binomial_distribution|binomial distribution]], where | + | $\text{Definition:}$ The '''Poisson distribution''' is a limiting case of the [[Theory_of_Stochastic_Signals/Binomial_Distribution#General_description_of_the_binomial_distribution|binomial distribution]], where |
| − | *on the one hand, the limit transitions $I → ∞$ and $p → 0$ are assumed, | + | *on the one hand, the limit transitions $I → ∞$ and $p → 0$ are assumed, |
| − | *additionally, it is assumed that the product $I · p = λ$ has a finite value. | + | *additionally, it is assumed that the product $I · p = λ$ has a finite value. |
| − | The parameter $λ$ gives the average number of "ones" in a fixed unit of time and is called the '''rate''' | + | The parameter $λ$ gives the average number of "ones" in a fixed unit of time and is called the '''rate'''. }} |
| − | Further, it should be noted: | + | Further, it should be noted: |
| − | *In contrast to the binomial distribution $(0 ≤ μ ≤ I)$ here the random quantity can take on arbitrarily large (integer, non-negative) values. | + | *In contrast to the binomial distribution $(0 ≤ μ ≤ I)$ here the random quantity can take on arbitrarily large (integer, non-negative) values. |
*This means that the set of possible values here is uncountable. | *This means that the set of possible values here is uncountable. | ||
| − | *But since no intermediate values can occur, this is also called a | + | *But since no intermediate values can occur, this is also called a "discrete distribution". |
| Line 25: | Line 25: | ||
$\text{Calculation rule:}$ | $\text{Calculation rule:}$ | ||
| − | Considering above limit transitions for the [[Theory_of_Stochastic_Signals/Binomial_Distribution#Probabilities_of_the_binomial_distribution|probabilities of the binomial distribution]], it follows for the '''Probabilities of Poisson Distribution''' : | + | *Considering above limit transitions for the [[Theory_of_Stochastic_Signals/Binomial_Distribution#Probabilities_of_the_binomial_distribution|probabilities of the binomial distribution]], it follows for the '''Probabilities of Poisson Distribution''': |
:$$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$ | :$$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$ | ||
| − | From this, after some algebraic transformations, we obtain: | + | *From this, after some algebraic transformations, we obtain: |
:$$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$}} | :$$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$}} | ||
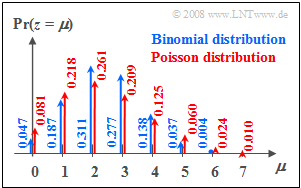
| − | [[File: EN_Sto_T_2_4_S1_neu.png |frame| Probabilities of the Poisson distribution | right]] | + | [[File: EN_Sto_T_2_4_S1_neu.png |frame| Probabilities of the Poisson distribution<br>compared to the binomial probabilities| right]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 1:}$ The probabilities | $\text{Example 1:}$ The probabilities | ||
| − | *of the binomial distribution with $I =6$, $p = 0.4$, and | + | *of the binomial distribution with $I =6$, $p = 0.4$, and |
*of the Poisson distribution with $λ = 2.4$ | *of the Poisson distribution with $λ = 2.4$ | ||
| − | can be seen in the graph on the right. | + | can be seen in the graph on the right. You can recognize: |
*Both distributions have the same mean $m_1 = 2.4$. | *Both distributions have the same mean $m_1 = 2.4$. | ||
| − | *In the Poisson distribution (red arrows and labels) the "outer values" are more probable than in the binomial distribution. | + | *In the Poisson distribution (red arrows and labels) the "outer values" are more probable than in the binomial distribution. |
| − | *In addition, random variables $z > 6$ are also possible with the Poisson distribution | + | *In addition, random variables $z > 6$ are also possible with the Poisson distribution, but their probabilities are also rather small at the chosen rate. }} |
| Line 49: | Line 49: | ||
$\text{Calculation rule:}$ | $\text{Calculation rule:}$ | ||
| − | The mean and rms of the Poisson distribution are obtained directly from the [[Theory_of_Stochastic_Signals/Binomial_Distribution#Moments_of_the_binomial_distribution|corresponding equations of the binomial distribution]] by twofold limiting: | + | *The '''mean''' and the '''rms value''' of the Poisson distribution are obtained directly from the [[Theory_of_Stochastic_Signals/Binomial_Distribution#Moments_of_the_binomial_distribution|corresponding equations of the binomial distribution]] by twofold limiting: |
:$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} I \cdot p= \lambda,$$ | :$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} I \cdot p= \lambda,$$ | ||
:$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$ | :$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$ | ||
| − | From this it can be seen that in the Poisson distribution | + | *From this it can be seen that in the Poisson distribution the varianc is always $σ^2 = m_1 = λ$. }} |
| Line 60: | Line 60: | ||
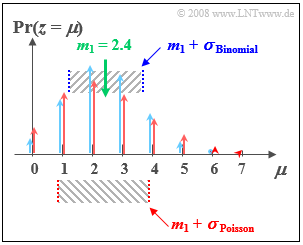
$\text{Example 2:}$ | $\text{Example 2:}$ | ||
| − | As in $\text{Example 1}$ | + | As in $\text{Example 1}$, here we compare: |
*the binomial distribution with $I =6$, $p = 0.4$, and | *the binomial distribution with $I =6$, $p = 0.4$, and | ||
| − | * | + | *the Poisson distribution with $λ = 2.4$. |
| Line 68: | Line 68: | ||
*Both distributions have exactly the same mean $m_1 = 2.4$. | *Both distributions have exactly the same mean $m_1 = 2.4$. | ||
| − | *For the Poisson distribution (marked red in the figure), the | + | *For the Poisson distribution (marked red in the figure), the rms value  (standard deviation) $σ ≈ 1.55$. |
| − | *In contrast, for the (blue) binomial distribution, the | + | *In contrast, for the (blue) binomial distribution, the rms value is only $σ = 1.2$.}} |
| − | With the interactive applet [[Applets:Binomial_and_Poisson_Distribution_(Applet)|Binomial | + | With the interactive HTML 5/JavaScript applet [[Applets:Binomial_and_Poisson_Distribution_(Applet)|"Binomial and Poisson Distribution"]] |
| + | *you can determine the probabilities and means (moments) of the Poisson distribution for any $λ$-values | ||
| + | *and visualize the similarities and differences compared to the binomial distribution. | ||
==Comparison of binomial distribution vs. Poisson distribution== | ==Comparison of binomial distribution vs. Poisson distribution== | ||
<br> | <br> | ||
| − | Now both the similarities and the differences between binomial and | + | Now both the similarities and the differences between binomial and Poisson distributed random variables shall be worked out again. |
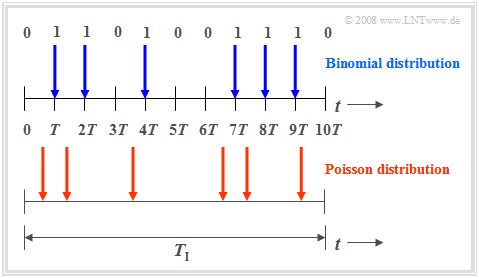
| − | + | [[File: EN_Sto_T_2_4_S3.png |right|frame| Scheme for binomial distribution (red) and Poisson distribution (blue)]] | |
| − | |||
| − | |||
| + | The '''binomial distribution''' is suitable for the description of such stochastic events, which are characterized by a given clock $T$. For example, for [[Examples_of_Communication_Systems/General_Description_of_ISDN|ISDN]] ("Integrated Services Digital Network") with $64 \ \rm kbit/s$ ⇒ the clock time $T \approx 15.6 \ \rm µ s$. | ||
| + | *'''Binary events only occur in this time grid'''. Such events are, for example, error-free $(e_i = 0)$ or errored $(e_i = 1)$ transmission of individual symbols. | ||
| + | *The binomial distribution now allows statistical statements about the number of transmission errors to be expected in a longer time interval $T_{\rm I} = I ⋅ T$ according to the upper diagram of the graph (time marked in blue). | ||
| − | |||
Also the '''Poisson distribution''' makes statements about the number of occurring binary events in a finite time interval: | Also the '''Poisson distribution''' makes statements about the number of occurring binary events in a finite time interval: | ||
| − | *If one assumes | + | *If one assumes the same observation period $T_{\rm I}$ and increases the number $I$ of subintervals more and more, then the clock time $T$, at which a new binary event ("0" or "1") can occur, becomes smaller and smaller. In the limiting case $T \to 0$. |
| − | *This means: In the Poisson distribution, the binary events are possible not only at discrete points | + | *This means: In the Poisson distribution, '''the binary events are possible''' not only at discrete time points given by a time grid, but '''at any time'''. The time diagram below illustrates this fact. |
| − | *In order to obtain on average during time $T_{\rm I}$ exactly as many "ones" as in the binomial distribution (in the example: six), however, the characteristic probability related to the infinitesimally small time interval $T$ must tend to zero | + | *In order to obtain on average during time $T_{\rm I}$ exactly as many "ones" as in the binomial distribution (in the example: six), however, the characteristic probability $p = {\rm Pr}( e_i = 1)$ related to the infinitesimally small time interval $T$ must tend to zero. |
| Line 96: | Line 98: | ||
The Poisson distribution is the result of a so-called [https://en.wikipedia.org/wiki/Poisson_point_process Poisson process]. Such a process is often used as a model for sequences of events that may occur at random times. Examples of such events include. | The Poisson distribution is the result of a so-called [https://en.wikipedia.org/wiki/Poisson_point_process Poisson process]. Such a process is often used as a model for sequences of events that may occur at random times. Examples of such events include. | ||
*the failure of equipment - an important task in reliability theory, | *the failure of equipment - an important task in reliability theory, | ||
| − | *the shot noise in optical transmission, and | + | *the shot noise in optical transmission, and |
*the start of telephone calls in a switching center ("teletraffic engineering"). | *the start of telephone calls in a switching center ("teletraffic engineering"). | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Example 3:}$ If ninety switching requests per minute $($ | + | $\text{Example 3:}$ If ninety switching requests per minute $($⇒ $λ = 1.5 \text{ per second})$ are received by a switching center on a long–term average, the probabilities $p_\mu$ that exactly $\mu$ connections occur in any one-second period are: |
:$$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$ | :$$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$ | ||
| − | This gives the numerical values $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, etc. | + | This gives the numerical values $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, etc. |
| − | From this, further characteristics can be derived: | + | From this, further characteristics can be derived: |
| − | *The distance $τ$ between two | + | *The distance $τ$ between two placement requests satisfies the [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#One-sided_exponential_distribution|exponential distribution]]. |
| − | *The mean time interval between two | + | *The mean time interval between two placement requests is ${\rm E}[\hspace{0.05cm}τ\hspace{0.05cm}] = 1/λ ≈ 0.667 \ \rm s$.}} |
Revision as of 15:06, 14 December 2021
Contents
Probabilities of the Poisson distribution
$\text{Definition:}$ The Poisson distribution is a limiting case of the binomial distribution, where
- on the one hand, the limit transitions $I → ∞$ and $p → 0$ are assumed,
- additionally, it is assumed that the product $I · p = λ$ has a finite value.
The parameter $λ$ gives the average number of "ones" in a fixed unit of time and is called the rate.
Further, it should be noted:
- In contrast to the binomial distribution $(0 ≤ μ ≤ I)$ here the random quantity can take on arbitrarily large (integer, non-negative) values.
- This means that the set of possible values here is uncountable.
- But since no intermediate values can occur, this is also called a "discrete distribution".
$\text{Calculation rule:}$
- Considering above limit transitions for the probabilities of the binomial distribution, it follows for the Probabilities of Poisson Distribution:
- $$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$
- From this, after some algebraic transformations, we obtain:
- $$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$
$\text{Example 1:}$ The probabilities
- of the binomial distribution with $I =6$, $p = 0.4$, and
- of the Poisson distribution with $λ = 2.4$
can be seen in the graph on the right. You can recognize:
- Both distributions have the same mean $m_1 = 2.4$.
- In the Poisson distribution (red arrows and labels) the "outer values" are more probable than in the binomial distribution.
- In addition, random variables $z > 6$ are also possible with the Poisson distribution, but their probabilities are also rather small at the chosen rate.
Moments of the Poisson distribution
$\text{Calculation rule:}$
- The mean and the rms value of the Poisson distribution are obtained directly from the corresponding equations of the binomial distribution by twofold limiting:
- $$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} I \cdot p= \lambda,$$
- $$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0} }\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$
- From this it can be seen that in the Poisson distribution the varianc is always $σ^2 = m_1 = λ$.
$\text{Example 2:}$
As in $\text{Example 1}$, here we compare:
- the binomial distribution with $I =6$, $p = 0.4$, and
- the Poisson distribution with $λ = 2.4$.
One can see from the accompanying sketch:
- Both distributions have exactly the same mean $m_1 = 2.4$.
- For the Poisson distribution (marked red in the figure), the rms value  (standard deviation) $σ ≈ 1.55$.
- In contrast, for the (blue) binomial distribution, the rms value is only $σ = 1.2$.
With the interactive HTML 5/JavaScript applet "Binomial and Poisson Distribution"
- you can determine the probabilities and means (moments) of the Poisson distribution for any $λ$-values
- and visualize the similarities and differences compared to the binomial distribution.
Comparison of binomial distribution vs. Poisson distribution
Now both the similarities and the differences between binomial and Poisson distributed random variables shall be worked out again.
The binomial distribution is suitable for the description of such stochastic events, which are characterized by a given clock $T$. For example, for ISDN ("Integrated Services Digital Network") with $64 \ \rm kbit/s$ ⇒ the clock time $T \approx 15.6 \ \rm µ s$.
- Binary events only occur in this time grid. Such events are, for example, error-free $(e_i = 0)$ or errored $(e_i = 1)$ transmission of individual symbols.
- The binomial distribution now allows statistical statements about the number of transmission errors to be expected in a longer time interval $T_{\rm I} = I ⋅ T$ according to the upper diagram of the graph (time marked in blue).
Also the Poisson distribution makes statements about the number of occurring binary events in a finite time interval:
- If one assumes the same observation period $T_{\rm I}$ and increases the number $I$ of subintervals more and more, then the clock time $T$, at which a new binary event ("0" or "1") can occur, becomes smaller and smaller. In the limiting case $T \to 0$.
- This means: In the Poisson distribution, the binary events are possible not only at discrete time points given by a time grid, but at any time. The time diagram below illustrates this fact.
- In order to obtain on average during time $T_{\rm I}$ exactly as many "ones" as in the binomial distribution (in the example: six), however, the characteristic probability $p = {\rm Pr}( e_i = 1)$ related to the infinitesimally small time interval $T$ must tend to zero.
Applications of the Poisson distribution
The Poisson distribution is the result of a so-called Poisson process. Such a process is often used as a model for sequences of events that may occur at random times. Examples of such events include.
- the failure of equipment - an important task in reliability theory,
- the shot noise in optical transmission, and
- the start of telephone calls in a switching center ("teletraffic engineering").
$\text{Example 3:}$ If ninety switching requests per minute $($⇒ $λ = 1.5 \text{ per second})$ are received by a switching center on a long–term average, the probabilities $p_\mu$ that exactly $\mu$ connections occur in any one-second period are:
- $$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$
This gives the numerical values $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, etc.
From this, further characteristics can be derived:
- The distance $τ$ between two placement requests satisfies the exponential distribution.
- The mean time interval between two placement requests is ${\rm E}[\hspace{0.05cm}τ\hspace{0.05cm}] = 1/λ ≈ 0.667 \ \rm s$.
Exercises for the chapter
Aufgabe 2.5: „Binomial” oder „Poisson”?