Aufgaben:Exercise 2.11: Envelope Demodulation of an SSB Signal

• Return to book

(Normalized) envelope in
Single-sideband modulation

Let us consider the transmission of the cosine signal

$$ q(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t)$$

according to the modulation method "USB–AM with carrier".  At the receiver, the high frequency is reset to the LF range with an   envelope demodulator .

The channel is assumed to be ideal such that the received signal    $r(t)$  is identical to the transmit signal  $s(t)$ .  With a sideband-to-carrier ratio

$$ \mu = \frac{A_{\rm N}}{2 \cdot A_{\rm T}}$$

the equivalent lowpass signal can be written as:

$$r_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + \mu \cdot {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right) \hspace{0.05cm}$$

The envelope – i.e., the magnitude of this complex signal – can be determined by geometric considerations.  Independent of the parameter  $μ$, one obtains:

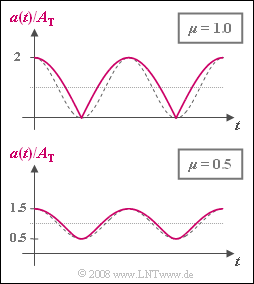
$$a(t ) = A_{\rm T} \cdot \sqrt{1+ \mu^2 + 2 \mu \cdot \cos(\omega_{\rm N} \cdot t)}\hspace{0.05cm}.$$

The time-independent envelope  $a(t)$  for  $μ = 1$  and  $μ = 0.5$  is shown in the graph.  In each case, the amplitude-matched cosine oscillations, which would be a prerequisite for distortion-free demodulation, are plotted as dashed comparison curves.

• The periodic signal $a(t)$  can be approximated by a  Fourier Series :

$$a(t ) = A_{\rm 0} + A_{\rm 1} \cdot \cos(\omega_{\rm N} \cdot t) + A_{\rm 2} \cdot \cos(2\omega_{\rm N} \cdot t)+ A_{\rm 3} \cdot \cos(3\omega_{\rm N} \cdot t)\hspace{0.05cm}+\text{...}$$

• The Fourier coefficients were determined using a simulation program.   With  $μ = 1$  the following values were obtained:

$$A_{\rm 0} = 1.273\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.849\,{\rm V},\hspace{0.3cm}A_{\rm 2} = -0.170\,{\rm V},\hspace{0.3cm} A_{\rm 3} = 0.073\,{\rm V},\hspace{0.3cm}A_{\rm 4} = 0.040\,{\rm V} \hspace{0.05cm}.$$

• Accordingly, for  $μ = 0.5$, the simulation yielded:

$$A_{\rm 0} = 1.064\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.484\,{\rm V},\hspace{0.3cm}A_{\rm 2} = 0.058\,{\rm V} \hspace{0.05cm}.$$

The values not given here can be ignored when calculating of the distortion factor.

• The sink signal  $v(t)$  is obtained from  $a(t)$  as follows:

$$v(t) = 2 \cdot \big [a(t ) - A_{\rm 0} \big ] \hspace{0.05cm}.$$

The factor of  $2$  corrects for the amplitude loss due to SSB-AM, while the subtraction of the DC signal coefficient  $A_0$  takes into account the influence of the high-pass within the envelope demodulator.

In questions  (1)  to  (3) , it is assumed that  $A_{\rm N} = 2 \ \rm V$, $A_{\rm T} = 1 \ \rm V$   ⇒   $μ = 1$ , whereas from question  (4) , $A_{\rm N} = A_{\rm T} = 1 \ \rm V$  should apply for the parameter  $μ = 0.5$.

Hints:

• This exercise belongs to the chapter  Single-Sideband Modulation.
• Particular reference is made to the page   Sideband-to-carrier ratio.
• Also compare your results to the rule of thumb which states that for the envelope demodulation of an SSB-AM signal with sideband-to-carrier ratio  $μ$ , the distortion factor is  $K ≈ μ/4$ .

Questions

1

Give the maximum and minimum values of the sink signal  $v(t)$  when  $μ = 1$ .

$v_{\rm max} \ = \ $ $\ \rm V$

$v_{\rm min} \ = \ $ $\ \rm V$

2

Calculate the distortion factor when  $μ = 1$.

$K \ = \ $ $\ \text{%}$

3

How can you recognize the nonlinear distortions in the present signal  $v(t)$?

	The lower cosine half-wave is more peaked than the upper one.
	The DC component  ${\rm Ε}\big[v(t)\big ] = 0$.

4

Give the maximum and minimum values of the sink signal  $v(t)$  when  $μ = 0.5$ .

$v_{\rm max} \ = \ $ $\ \rm V$

$v_{\rm min} \ = \ $ $\ \rm V$

5

Calculate the distortion factor when  $μ = 0.5$.

$K \ = \ $ $\ \text{%}$

6

What is the upper bound  $K_{\rm max}$  of the distortion factor in DSB-AM with  $m = 0.5$  and envelope demodulation, if one sideband is completely damped by the channel.

$K_{\rm max} \ = \ $ $\ \text{%}$

Solution

Solution

(1)  The maximum value   $a_{\rm max} = 2\ \rm V$  and the minimum value   $a_{\rm min} = 0$  can be read of the graph or calculated using the equation given:

$$ a_{\rm max} = A_{\rm T} \cdot \sqrt{1+ \mu^2 + 2 \mu}= A_{\rm T} \cdot (1+ \mu) = 2\,{\rm V} \hspace{0.05cm},$$

$$a_{\rm min} = A_{\rm T} \cdot \sqrt{1+ \mu^2 - 2 \mu}= A_{\rm T} \cdot (1- \mu) = 0 \hspace{0.05cm}.$$

• Für die beiden Extremwerte des Sinkensignals folgt daraus:

$$ v_{\rm max} = 2 \cdot [a_{\rm max} - A_{\rm 0}] = 2 \cdot [2\,{\rm V} - 1.273\,{\rm V}] \hspace{0.15cm}\underline {=1.454\,{\rm V}}\hspace{0.05cm},$$

$$ v_{\rm min} = -2 \cdot A_{\rm 0} \hspace{0.15cm}\underline {= -2.546\,{\rm V}}\hspace{0.05cm}.$$

(2)  Unter Vernachlässigung der Fourierkoeffizienten  $A_5$,  $A_6$,  usw. erhält man:

$$K = \frac{\sqrt{A_2^2 + A_3^2+ A_4^2 }}{A_1}= \frac{\sqrt{0.170^2 + 0.073^2 + 0.040^2 }{\,\rm V}}{0.849\,{\rm V}}\hspace{0.15cm}\underline { \approx 22.3 \%}.$$

• Die Näherung  $K ≈ μ/4$  liefert hier den Wert $25\%$.

(3)  Nur der erste Lösungsvorschlag ist richtig.

• Aufgrund des Hochpasses innerhalb des Hüllkurvendemodulators wäre der Gleichsignalanteil auch dann Null, wenn keine Verzerrungen vorlägen.

(4)  Analog zur Teilaufgabe  (1)  gilt hier:

$$v_{\rm max} = 2 \cdot [a_{\rm max} - A_{\rm 0}] = 2 \cdot [1.5\,{\rm V} - 1.064\,{\rm V}] \hspace{0.15cm}\underline {= 0.872\,{\rm V}}\hspace{0.05cm},$$

$$ v_{\rm min} = -2 \cdot A_{\rm 0} \hspace{0.15cm}\underline {= -2.128\,{\rm V}}\hspace{0.05cm}.$$

(5)  Bei kleinerem Seitenband–zu–Träger–Verhältnis ergibt sich auch ein kleinerer Klirrfaktor:

$$K = \frac{0.058{\,\rm V}}{0.484\,{\rm V}}\hspace{0.15cm}\underline { \approx 12 \%}.$$

• Die einfache Näherung  $K ≈ μ/4$  ergibt hier  $12.5\%$.
• Daraus kann geschlossen werden, dass die angegebene Faustformel bei kleinerem  $μ$  genauer ist.

(6)  Der Klirrfaktor ist dann am größten, wenn eines der Seitenbänder völlig abgeschnitten wird. 

• Da aber der Hüllkurvendemodulator keinerlei Kenntnis davon hat, ob
  • eine ESB–AM, oder
  • eine durch den Kanal extrem beeinträchtigte ZSB–AM

vorliegt, gibt  $K_{\rm max} ≈ μ/4$  gleichzeitig eine obere Schranke für die ZSB–AM an.

• Ein Vergleich der Parameter  $m = A_{\rm N}/A_{\rm T}$  und  $μ = A_{\rm N}/(2A_{\rm T})$  führt zum Ergebnis:

$$K_{\rm max} = \frac{\mu}{4} = \frac{m}{8} \hspace{0.15cm}\underline {=6.25 \%}.$$