Difference between revisions of "Aufgaben:Exercise 3.2: CDF for Exercise 3.1"
From LNTwww
| Line 75: | Line 75: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Since $x$ is | + | '''(1)''' Since the continuous valued random variable $x$ is limited to the range $|\hspace{0.05cm}x\hspace{0.05cm}< 2|$, <u>all three given statements</u> are correct. |
| − | '''(2)''' Only <u>statements 2 and 3</u> are correct here: | + | '''(2)''' Only <u>statements 2 and 3</u> are correct here: |
| − | *For a discrete random variable, the distribution function increases only weakly monotonically. | + | *For a discrete valued random variable, the cumulative distribution function increases only weakly monotonically. |
| − | * That means: Except for unit steps, there are only horizontal sections of the CDF. | + | * That means: Except for unit steps, there are only horizontal sections of the CDF. |
| − | *Since at the unit step points the right-hand side limit value | + | *Since at the unit step points the right-hand side limit value ⇒ $F_y(-2) = 0.1$, i.e. not equal to zero. |
| Line 88: | Line 88: | ||
'''(3)''' The CDF $F_x(r)$ is calculated as the integral from $-\infty$ to $r$ over the PDF $f_x(x)$. | '''(3)''' The CDF $F_x(r)$ is calculated as the integral from $-\infty$ to $r$ over the PDF $f_x(x)$. | ||
| − | Due to symmetry, herefore can be written in the range $0 \le r \le +2$ | + | *Due to symmetry, herefore can be written in the range $0 \le r \le +2$: |
:$$F_{x} (r) =\frac{1}{2} + \int_{0}^{r} f_x(x)\;{\rm d}x = \frac{1}{2} + \int_{0}^{ r} {1}/{2}\cdot \cos^2 ({\pi}/{4}\cdot x)\;{\rm d}x.$$ | :$$F_{x} (r) =\frac{1}{2} + \int_{0}^{r} f_x(x)\;{\rm d}x = \frac{1}{2} + \int_{0}^{ r} {1}/{2}\cdot \cos^2 ({\pi}/{4}\cdot x)\;{\rm d}x.$$ | ||
| − | In the same way as for the subtask '''(7)''' of Exercise 3.1, we thus obtain: | + | *In the same way as for the subtask '''(7)''' of Exercise 3.1, we thus obtain: |
:$$F_{x} (r) =\frac{1}{2} + \frac{ r}{ 4} + \frac{1}{2 \pi} \cdot \sin({\pi}/{2}\cdot r),$$ | :$$F_{x} (r) =\frac{1}{2} + \frac{ r}{ 4} + \frac{1}{2 \pi} \cdot \sin({\pi}/{2}\cdot r),$$ | ||
:$$F_{x} (r=0) =\rm \frac{1}{2} + \rm \frac{1}{2 \pi} \cdot\rm sin(\rm 0)\hspace{0.15cm}{= 0.500},$$ | :$$F_{x} (r=0) =\rm \frac{1}{2} + \rm \frac{1}{2 \pi} \cdot\rm sin(\rm 0)\hspace{0.15cm}{= 0.500},$$ | ||
| Line 98: | Line 98: | ||
| − | '''(4)''' Because of the point symmetry around $r=0$ resp. $F_{x} (0) = 1/2$ and because of $\sin(-x) = -\sin(x)$ this formula holds in the whole domain, as the following control calculation shows: | + | '''(4)''' Because of the point symmetry around $r=0$ resp. $F_{x} (0) = 1/2$ and because of $\sin(-x) = -\sin(x)$ this formula holds in the whole domain, as the following control calculation shows: |
:$$F_{x} (r=-2) =\rm \frac{1}{2} - \frac{\rm1}{\rm 2} - \rm \frac{1}{2 \pi} \cdot\rm sin(\pi)=0,$$ | :$$F_{x} (r=-2) =\rm \frac{1}{2} - \frac{\rm1}{\rm 2} - \rm \frac{1}{2 \pi} \cdot\rm sin(\pi)=0,$$ | ||
:$$F_{x} (r=-1) =\rm \frac{1}{2} - \frac{\rm1}{\rm 4} - \rm \frac{1}{2 \pi} \cdot\rm sin({\pi}/{2})\hspace{0.15cm}\underline{= 0.091}.$$ | :$$F_{x} (r=-1) =\rm \frac{1}{2} - \frac{\rm1}{\rm 4} - \rm \frac{1}{2 \pi} \cdot\rm sin({\pi}/{2})\hspace{0.15cm}\underline{= 0.091}.$$ | ||
| − | '''(5)''' For the probability that $x$ lies between $-1$ and $+1$ | + | '''(5)''' For the probability that $x$ lies between $-1$ and $+1$: |
:$${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}|< 1)= F_{x}(+1) - F_{ x}(-1)= 0.909-0.091\hspace{0.15cm}\underline{= 0.818}.$$ | :$${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}|< 1)= F_{x}(+1) - F_{ x}(-1)= 0.909-0.091\hspace{0.15cm}\underline{= 0.818}.$$ | ||
| − | *This result agrees exactly with the result of the subtask '''(7)''' of Exercise 3.1 & | + | *This result agrees exactly with the result of the subtask '''(7)''' of Exercise 3.1 which was obtained by direct integration üover the WDF. |
| − | '''(6)''' The | + | |
| + | '''(6)''' The CDF of the discrete valued random variable $y$ at the location $y =0$ is the sum of the probabilities of $-2$, $-1$ and $0$. So: | ||
:$$F_y(r = 0)\hspace{0.15cm}\underline{= 0.7}.$$ | :$$F_y(r = 0)\hspace{0.15cm}\underline{= 0.7}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 15:18, 4 January 2022
The same conditions apply as for Exercise 3.1.
- The PDF of the continuous valued random variable is identically zero in the ranges $|x| > 2$.
- In the range $-2 \le x \le +2$ holds:
- $$f_x(x)={1}/{2}\cdot \cos^2({\pi}/{4}\cdot x).$$
- The discrete valued random variable $y$ is limited too to the range $\pm 2$ Here, the following probabilities apply:
- $${\rm \Pr}(y=0)=0.4,$$
- $${\rm \Pr}(y=+1)={\rm \Pr}(y=-1)=0.2,$$
- $${\rm \Pr}(y=+2)={\rm \Pr}(y=-2)=0.1.$$
Hints:
- The exercise belongs to the chapter Cumulative Distribution Function.
- The topic of this chapter is illustrated with examples in the (German language) learning video
"Zusammenhang zwischen WDF und VTF" $\Rightarrow$ "Relationship between PDF and CDF". - Given the following equation:
- $$\int \cos^{\rm 2}( ax)\, {\rm d}x=\frac{x}{2}+\frac{1}{4 a}\cdot \sin(2 ax).$$
Questions
Solution
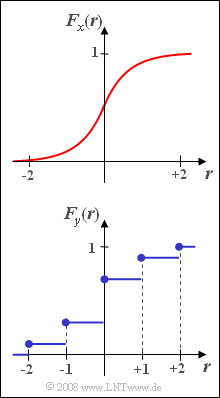
(1) Since the continuous valued random variable $x$ is limited to the range $|\hspace{0.05cm}x\hspace{0.05cm}< 2|$, all three given statements are correct.
(2) Only statements 2 and 3 are correct here:
- For a discrete valued random variable, the cumulative distribution function increases only weakly monotonically.
- That means: Except for unit steps, there are only horizontal sections of the CDF.
- Since at the unit step points the right-hand side limit value ⇒ $F_y(-2) = 0.1$, i.e. not equal to zero.
(3) The CDF $F_x(r)$ is calculated as the integral from $-\infty$ to $r$ over the PDF $f_x(x)$.
- Due to symmetry, herefore can be written in the range $0 \le r \le +2$:
- $$F_{x} (r) =\frac{1}{2} + \int_{0}^{r} f_x(x)\;{\rm d}x = \frac{1}{2} + \int_{0}^{ r} {1}/{2}\cdot \cos^2 ({\pi}/{4}\cdot x)\;{\rm d}x.$$
- In the same way as for the subtask (7) of Exercise 3.1, we thus obtain:
- $$F_{x} (r) =\frac{1}{2} + \frac{ r}{ 4} + \frac{1}{2 \pi} \cdot \sin({\pi}/{2}\cdot r),$$
- $$F_{x} (r=0) =\rm \frac{1}{2} + \rm \frac{1}{2 \pi} \cdot\rm sin(\rm 0)\hspace{0.15cm}{= 0.500},$$
- $$F_{x} (r=1) =\rm \frac{1}{2} + \frac{\rm 1}{\rm 4} + \rm \frac{1}{2 \pi}\cdot \rm sin({\pi}/{2})\hspace{0.15cm}\underline{=0.909},$$
- $$F_{x} (r=2) =\rm \frac{1}{2} + \frac{\rm1}{\rm 2} + \rm \frac{1}{2 \pi} \cdot \rm sin(\pi)\hspace{0.15cm}{= 1.000}.$$
(4) Because of the point symmetry around $r=0$ resp. $F_{x} (0) = 1/2$ and because of $\sin(-x) = -\sin(x)$ this formula holds in the whole domain, as the following control calculation shows:
- $$F_{x} (r=-2) =\rm \frac{1}{2} - \frac{\rm1}{\rm 2} - \rm \frac{1}{2 \pi} \cdot\rm sin(\pi)=0,$$
- $$F_{x} (r=-1) =\rm \frac{1}{2} - \frac{\rm1}{\rm 4} - \rm \frac{1}{2 \pi} \cdot\rm sin({\pi}/{2})\hspace{0.15cm}\underline{= 0.091}.$$
(5) For the probability that $x$ lies between $-1$ and $+1$:
- $${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}|< 1)= F_{x}(+1) - F_{ x}(-1)= 0.909-0.091\hspace{0.15cm}\underline{= 0.818}.$$
- This result agrees exactly with the result of the subtask (7) of Exercise 3.1 which was obtained by direct integration üover the WDF.
(6) The CDF of the discrete valued random variable $y$ at the location $y =0$ is the sum of the probabilities of $-2$, $-1$ and $0$. So:
- $$F_y(r = 0)\hspace{0.15cm}\underline{= 0.7}.$$