Theory of Stochastic Signals/Exponentially Distributed Random Variables

1. Theory of Stochastic Signals
2. Continuous Random Variables
3. Exponentially Distributed Random Variables

• Previous page
• Next page

• Previous page
• Next page

One-sided exponential distribution

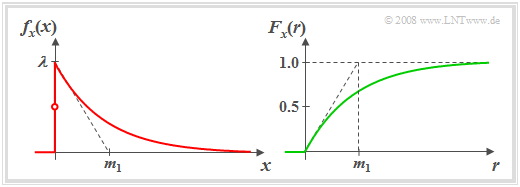
$\text{Definition:}$  A continuous random variable  $x$  is called (one-sided)  exponentially distributed if it can take only non–negative values and the PDF for  $x>0$  has the following shape:

$$f_x(x)=\it \lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}.$$

PDF and CDF of an exponentially distributed random variable

The left image shows the  probability density function  (PDF) of such an exponentially distributed random variable  $x$.  Highlight:

• The larger the distribution parameter  $λ$  is, the steeper the decay occurs.
• By definition  $f_{x}(0) = λ/2$, i.e. the mean of left-hand limit  $(0)$  and right-hand limit  $(\lambda)$.

For the  cumulative distribution function  (right graph), we obtain for  $r > 0$  by integration over the PDF:

$$F_{x}(r)=1-\rm e^{\it -\lambda\hspace{0.05cm}\cdot \hspace{0.03cm} r}.$$

The  moments  of the one-sided exponential distribution are generally equal to  

$$m_k = k!/λ^k.$$

From this and from Steiner's theorem, we get for the mean and the rms:

$$m_1={1}/{\lambda},$$

$$\sigma=\sqrt{m_2-m_1^2}=\sqrt{\frac{2}{\lambda^2}-\frac{1}{\lambda^2}}={1}/{\lambda}.$$

$\text{Example 1:}$  The exponential distribution has great importance for reliability studies, and the term "lifetime distribution" is also commonly used in this context.

• In these applications, the random variable is often the time  $t$ that elapses before a component fails.
• Furthermore, it should be noted that the exponential distribution is closely related to the  Poisson distribution .

Transformation of random variables

To generate such an exponentially distributed random variable on a digital computer, for example, a  nonlinear transformation  The underlying principle is first stated here in general terms.

$\text{Procedure:}$  If a continuous random variable  $u$  possesses the PDF  $f_{u}(u)$, then the probability density function of the random variable transformed at the nonlinear characteristic  $x = g(u)$  $x$ holds:

$$f_{x}(x)=\frac{f_u(u)}{\mid g\hspace{0.05cm}'(u)\mid}\Bigg \vert_{\hspace{0.1cm} u=h(x)}.$$

Here  $g\hspace{0.05cm}'(u)$  denotes the derivative of the characteristic curve  $g(u)$  and  $h(x)$  gives the inverse function to  $g(u)$  .

• The above equation is valid, however, only under the condition that the derivative  $g\hspace{0.03cm}'(u) \ne 0$  .
• For a characteristic with horizontal sections  $(g\hspace{0.05cm}'(u) = 0)$  additional Dirac functions appear in the PDF if the input quantity has components in the range.
• The weights of these Dirac functions are equal to the probabilities that the input quantity lies in these domains.

To transform random variables

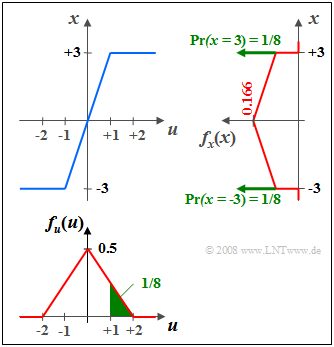
$\text{Example 2:}$  Given a random variable distributed between  $-2$  and  $+2$  triangularly  $u$  on a nonlinearity with characteristic  $x = g(u)$,

• which, in the range  $\vert u \vert ≤ 1$  triples the input values,  and
• mapping all values  $\vert u \vert > 1$  to  $x = \pm 3$  depending on the sign,

then the PDF $f_{x}(x)$ sketched on the right is obtained.

Please note:

(1)   Due to the amplification by a factor of  $3$  $f_{x}(x)$  is wider and lower than $f_{u}(u) by this factor.$

(2)   The two horizontal limits of the characteristic at  $u = ±1$  lead to the two Dirac functions at  $x = ±3$, each with weight  $1/8$.

(3)   The weight  $1/8$  corresponds to the green areas in the PDF $f_{u}(u).$

Generation of an exponentially distributed random variable

$\text{Procedure:}$  Now we assume that the random variable to be transformed  $u$  is uniformly distributed between  $0$  (inclusive) and  $1$  (exclusive).  Moreover, we consider the monotonically increasing characteristic curve

$$x=g_1(u) =\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{1-\it u}).$$

It can be shown that by this characteristic  $x=g_1(u)$  a one-sided exponentially distributed random variable  $x$  with the following PDF arises 
(derivation see next page):

$$f_{x}(x)=\lambda\cdot\rm e^{\it -\lambda \hspace{0.05cm}\cdot \hspace{0.03cm} x}\hspace{0.2cm}{\rm for}\hspace{0.2cm} {\it x}>0.$$

• For  $x = 0$  the PDF value is half  $(\lambda/2)$.
• Negative  $x$ values do not occur because for  $0 ≤ u < 1$  the argument of the (natural) logarithm function does not become smaller than  $1$.

By the way, the same PDF is obtained with the monotonically decreasing characteristic curve

$$x=g_2(u)=\frac{1}{\lambda}\cdot \rm ln \ (\frac{1}{\it u})=-\frac{1}{\lambda}\cdot \rm ln(\it u \rm ).$$

Please note:

• When using a computer implementation corresponding to the first transformation characteristic  $x=g_1(u)$  the value  $u = 1$  must be excluded.
• If one uses the second transformation characteristic  $x=g_2(u)$, on the other hand, the value  $u =0$  must be excluded.

The (German) learning video  Erzeugung einer Exponentialverteilung  $\Rightarrow$ Generation of an exponential distribution, shall clarify the transformations derived here.

Derivation of the corresponding transformation characteristic

$\text{Exercise:}$  Now derive the transformation characteristic  $x = g_1(u)= g(u)$  already used on the last page, which is derived from a random variable  equally distributed between  $0$  and  $1$  ; $u$  with the probability density function (PDF)  $f_{u}(u)$  forms a one-sided exponentially distributed random variable  $x$  with the PDF  $f_{x}(x)$  :

$$f_{u}(u)= \left\{ \begin{array}{*{2}{c} } 1 & \rm if\hspace{0.3cm} 0 < {\it u} < 1,\\ 0.5 & \rm if\hspace{0.3cm} {\it u} = 0, {\it u} = 1,\ 0 & \rm else, \end{array} \right. \hspace{0.5cm}\rightarrow \hspace{0.5cm} f_{x}(x)= \left\{ \begin{array}{*{2}{c} } \lambda\cdot\rm e^{\it -\lambda\hspace{0.03cm} \cdot \hspace{0.03cm} x} & \rm if\hspace{0.3cm} {\it x} > 0,\ \lambda/2 & \rm if\hspace{0.3cm} {\it x} = 0 ,\ 0 & \rm if\hspace{0.3cm} {\it x} < 0. \ \end{array} \right.$$

$\text{Solution:}$ 

(1)  Starting from the general transformation equation.

$$f_{x}(x)=\frac{f_{u}(u)}{\mid g\hspace{0.05cm}'(u) \mid }\Bigg \vert _{\hspace{0.1cm} u=h(x)}$$

is obtained by converting and substituting the given PDF $f_{ x}(x):$

$$\mid g\hspace{0.05cm}'(u)\mid\hspace{0.1cm}=\frac{f_{u}(u)}{f_{x}(x)}\Bigg \vert _{\hspace{0.1cm} x=g(u)}= {1}/{\lambda} \cdot {\rm e}^{\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}g(u)}.$$

Here  $x = g\hspace{0.05cm}'(u)$  gives the derivative of the characteristic curve, which we assume to be monotonically increasing.

(2)  With this assumption we get  $\vert g\hspace{0.05cm}'(u)\vert = g\hspace{0.05cm}'(u) = {\rm d}x/{\rm d}u$  and the differential equation  ${\rm d}u = \lambda\ \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}\, {\rm d}x$  with solution  $u = K - {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}.$

(3)  From the condition that the input quantity  $u =0$  should lead to the output value  $x =0$ , we obtain for the constant  $K =1$  and thus  $u = 1- {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm} x}.$

(4)  Solving this equation for  $x$  yields the equation given in front:

$$x = g_1(u)= \frac{1}{\lambda} \cdot {\rm ln} \left(\frac{1}{1 - u} \right) .$$

• In a computer implementation, however, ensure that the critical value  $1$  is excluded for the equally distributed input variable  $u$   
• This, however, has (almost) no effect on the final result.

Two-sided exponential distribution - Laplace distribution

Closely related to the exponential distribution is the so-called  Laplace distrubtion  with the probability density function

$$f_{x}(x)=\frac{\lambda}{2}\cdot\rm e^{\it -\lambda \hspace{0.05cm} \cdot \hspace{0.05cm} | x|}.$$

The Laplace distribution is a  two-sided exponential distribution that approximates sufficiently well, in particular, the amplitude distribution of speech– and music signals.

• The moments  $k$–th order   ⇒   $m_k$  of the Laplace distribution agree with those of the exponential distribution for even  $k$  .
• For odd  $k$  on the other hand, the (symmetric) Laplace distribution always yields  $m_k= 0$.

For generation one uses a between  $±1$  equally distributed random variable  $v$  (where  $v = 0$  must be excluded)  and the transformation characteristic curve

$$x=\frac{{\rm sign}(v)}{\lambda}\cdot \rm ln(\it v \rm ).$$

Further notes:

• From the  Exercise 3.8  one can see further properties of the Laplace distribution.

• In the (German) learning video  Wahrscheinlichkeit und WDF  $\Rightarrow$ Probability and PDF, it is shown which meaning the Laplace distribution has for the description of speech– and music signals.
• With the applet  PDF, CDF and Moments  you can display the characteristics  $($PDF, CDF, Moments$)$  of exponential and Laplace distributions.
• We also refer you to the applet  Two-dimensional Laplace random quantities .

Exercises for the chapter

Exercise 3.8: Amplification and Limitation

Exercise 3.8Z: Circle (Ring) Area

Exercise 3.9: Characteristic Curve for Cosine PDF

Exercise 3.9Z: Sine Transformation