Difference between revisions of "Aufgaben:Exercise 4.16Z: Multi-dimensional Data Reduction"
m (Guenter moved page Exercise 4.16Z: Multidimensional Data Reduction to Exercise 4.16Z: Multi-dimensional Data Reduction) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID678__Sto_Z_4_16.png|right|frame| | + | [[File:P_ID678__Sto_Z_4_16.png|right|frame|Matrices $\mathbf{K_y}$ and $\mathbf{K_z}$ ]] |
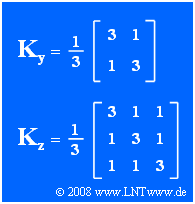
| − | We consider Gaussian zero mean random variables $\mathbf{x}$, $\mathbf{y}$ and $\mathbf{z}$ with dimensions $N= 1$, $N= 2$ and $N= 3$: | + | We consider Gaussian zero mean random variables $\mathbf{x}$, $\mathbf{y}$ and $\mathbf{z}$ with dimensions $N= 1$, $N= 2$ and $N= 3$: |
| − | * The one-dimensional random variable $\mathbf{x}$ is characterized by the variance $\sigma^2 = 1$ and the standard deviation $\sigma = 1$ respectively. <br>Because of the dimension $N= 1$ $\mathbf{x} = x$ | + | * The one-dimensional random variable $\mathbf{x}$ is characterized by the variance $\sigma^2 = 1$ and the standard deviation $\sigma = 1$ respectively. <br>Because of the dimension $N= 1$ ⇒ $\mathbf{x} = x$. |
* The correlation coefficient between the components $y_1$ and $y_2$ of the 2D random variable $\mathbf{y}$ is $\rho = 1/3$ $($see matrix $\mathbf{K_y})$. <br>$y_1$ and $y_2$ also have the standard deviation $\sigma = 1$. | * The correlation coefficient between the components $y_1$ and $y_2$ of the 2D random variable $\mathbf{y}$ is $\rho = 1/3$ $($see matrix $\mathbf{K_y})$. <br>$y_1$ and $y_2$ also have the standard deviation $\sigma = 1$. | ||
| Line 12: | Line 12: | ||
| − | If one quantizes the random variable $\mathbf{x}$ in the range between $-4$ and $+4$ with interval width $\Delta_x = 1/32$, there are altogether $N_1 = 256$ different quantization values, for whose transmission thus $n_1 = 8\ \rm {bit}$ would be needed. | + | If one quantizes the random variable $\mathbf{x}$ in the range between $-4$ and $+4$ with interval width $\Delta_x = 1/32$, there are altogether $N_1 = 256$ different quantization values, for whose transmission thus $n_1 = 8\ \rm {bit}$ would be needed. |
| − | Similarly, the random variable $\mathbf{y}$ results in a total of $N_2 = 256^2 = 65536$ different quantized value pairs, if the correlation between $y_1$ and $y_2$ is not taken into account. | + | Similarly, the random variable $\mathbf{y}$ results in a total of $N_2 = 256^2 = 65536$ different quantized value pairs, if the correlation between $y_1$ and $y_2$ is not taken into account. |
| − | Exploiting this correlation– for example, by coordinate transformation from the original system $(y_1, y_2)$ to the new system $(\eta_1, \eta_2)$ – results in a smaller number $N_2\hspace{0.01cm}'$ of quantized value pairs. | + | Exploiting this correlation – for example, by coordinate transformation from the original system $(y_1, y_2)$ to the new system $(\eta_1, \eta_2)$ – results in a smaller number $N_2\hspace{0.01cm}'$ of quantized value pairs. |
| − | *Here, it is to be considered that each component is to be quantized according to its respective | + | *Here, it is to be considered that each component is to be quantized according to its respective standard deviation $(\sigma_1$ resp. $\sigma_2)$ in the range of $-4$ to $+4$ and the quantization intervals should be the same in both directions: $\Delta_x = \Delta_y =1/32$. |
| − | *We denote the quotient $N_2\hspace{0.01cm}'/N_2$ as the data reduction factor with respect to the | + | *We denote the quotient $N_2\hspace{0.01cm}'/N_2$ as the data reduction factor with respect to the two-dimensional random variable $\mathbf{y}$. |
| − | *In analogous definition $N_3'/N_3$ is the corresponding reduction factor of the | + | *In analogous definition $N_3'/N_3$ is the corresponding reduction factor of the three-dimensional random variable $\mathbf{z}$ for $\Delta_x = \Delta_y =\Delta_z =1/32.$ |
*Note that in both cases the smallest possible value of this quotient would be favorable. | *Note that in both cases the smallest possible value of this quotient would be favorable. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 35: | Line 31: | ||
Hints: | Hints: | ||
*The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables|Generalization to N-Dimensional Random Variables]]. | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables|Generalization to N-Dimensional Random Variables]]. | ||
| − | *In particular, reference is made to the | + | *In particular, reference is made to the section [[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables#Eigenvalues_and_eigenvectors|Eigenvalues and Eigenvectors]] . |
| − | *Some basics on the application of vectors and matrices can be found on the pages [[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables#Basics_of_matrix_operations:_Determinant_of_a_matrix|Determinant of a Matrix]] | + | *Some basics on the application of vectors and matrices can be found on the pages |
| − | + | **[[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables#Basics_of_matrix_operations:_Determinant_of_a_matrix|Determinant of a Matrix]], | |
| − | *The equation | + | **[[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables#Basics_of_matrix_operations:_Inverse_of_a_matrix|Inverse of a Matrix]] . |
| + | *The equation for determination the eigenvalues of $\mathbf{K_z}$ is: $\lambda^3 - 3 \lambda^2 + {24}/{9}\lambda - {20}/{27} = 0.$ | ||
*One of the three solutions of this equation is $\lambda_1 = 5/3$. | *One of the three solutions of this equation is $\lambda_1 = 5/3$. | ||
| Line 51: | Line 48: | ||
| − | {What is the data reduction factor for the | + | {What is the data reduction factor for the two-dimensional random variable $\mathbf{y}$? |
|type="{}"} | |type="{}"} | ||
$N_2\hspace{0.01cm}'/N_2 \ = $ { 0.943 3% } | $N_2\hspace{0.01cm}'/N_2 \ = $ { 0.943 3% } | ||
| Line 62: | Line 59: | ||
| − | {What is the data reduction factor for the | + | {What is the data reduction factor for the three-dimensional random variable $\mathbf{z}$? |
|type="{}"} | |type="{}"} | ||
$N_3\hspace{0.01cm}'/N_3 \ = $ { 0.861 3% } | $N_3\hspace{0.01cm}'/N_3 \ = $ { 0.861 3% } | ||
Revision as of 15:42, 29 March 2022
We consider Gaussian zero mean random variables $\mathbf{x}$, $\mathbf{y}$ and $\mathbf{z}$ with dimensions $N= 1$, $N= 2$ and $N= 3$:
- The one-dimensional random variable $\mathbf{x}$ is characterized by the variance $\sigma^2 = 1$ and the standard deviation $\sigma = 1$ respectively.
Because of the dimension $N= 1$ ⇒ $\mathbf{x} = x$.
- The correlation coefficient between the components $y_1$ and $y_2$ of the 2D random variable $\mathbf{y}$ is $\rho = 1/3$ $($see matrix $\mathbf{K_y})$.
$y_1$ and $y_2$ also have the standard deviation $\sigma = 1$.
- The statistics of the three-dimensional random variable $\mathbf{z}$ is completely determined by the correlation matrix $\mathbf{K_z}$ .
If one quantizes the random variable $\mathbf{x}$ in the range between $-4$ and $+4$ with interval width $\Delta_x = 1/32$, there are altogether $N_1 = 256$ different quantization values, for whose transmission thus $n_1 = 8\ \rm {bit}$ would be needed.
Similarly, the random variable $\mathbf{y}$ results in a total of $N_2 = 256^2 = 65536$ different quantized value pairs, if the correlation between $y_1$ and $y_2$ is not taken into account.
Exploiting this correlation – for example, by coordinate transformation from the original system $(y_1, y_2)$ to the new system $(\eta_1, \eta_2)$ – results in a smaller number $N_2\hspace{0.01cm}'$ of quantized value pairs.
- Here, it is to be considered that each component is to be quantized according to its respective standard deviation $(\sigma_1$ resp. $\sigma_2)$ in the range of $-4$ to $+4$ and the quantization intervals should be the same in both directions: $\Delta_x = \Delta_y =1/32$.
- We denote the quotient $N_2\hspace{0.01cm}'/N_2$ as the data reduction factor with respect to the two-dimensional random variable $\mathbf{y}$.
- In analogous definition $N_3'/N_3$ is the corresponding reduction factor of the three-dimensional random variable $\mathbf{z}$ for $\Delta_x = \Delta_y =\Delta_z =1/32.$
- Note that in both cases the smallest possible value of this quotient would be favorable.
Hints:
- The exercise belongs to the chapter Generalization to N-Dimensional Random Variables.
- In particular, reference is made to the section Eigenvalues and Eigenvectors .
- Some basics on the application of vectors and matrices can be found on the pages
- The equation for determination the eigenvalues of $\mathbf{K_z}$ is: $\lambda^3 - 3 \lambda^2 + {24}/{9}\lambda - {20}/{27} = 0.$
- One of the three solutions of this equation is $\lambda_1 = 5/3$.
Questions
Solution
- $${\rm det}\left[ \begin{array}{cc} 1- \lambda & 1/3 \ 1/3 & 1- \lambda \end{array} \right] = (1-\lambda)^2 -{1}/{9} = 0 \hspace{0.3cm}\rightarrow \hspace{0.3cm}\lambda^2 -2\lambda+ {8}/{9}= 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\lambda_{1/2}= 1 \pm \sqrt{1-{8}/{9}}= 1 \pm {1}/{3}.$$
- The eigenvalues of this $2\times2$ matrix are thus $\lambda_1 = 4/3\hspace{0.15cm}\underline{=1.333}$ and $\lambda_2 = 2/3\hspace{0.15cm}\underline{=0.667}$.
(2) Without considering correlations, there are $N_2 = \left({8}/{ \Delta_x}\right)^2= 256^2 = 65536$ different pairs of values.
- Taking into account the correlations and the fact that the two components created by coordinate rotation $\eta_1$ and $\eta_2$ are each in the range $-4\sigma_1$ to $+4\sigma_1$ $($bzw. from $-4\sigma_2$ to $+4\sigma_2)$ ) are to be quantized, one obtains
- $$N_2\hspace{0.01cm}' = \frac{8 \hspace{0.05cm}\sigma_1}{\it \Delta_x}\cdot\frac{8 \hspace{0.05cm}\sigma_2}{\it \Delta_y}= N_2 \cdot \sigma_1 \cdot \sigma_2 .$$
- The quotient is thus with $\sigma_1^2 = \lambda_1$ and $\sigma_2^2 = \lambda_2$:
- $${N_2\hspace{0.01cm}'}/{N_2} = \sigma_1 \cdot \sigma_2 = \sqrt{{4}/{3}} \cdot \sqrt{{2}/{3}} = \frac{2 \cdot \sqrt{2}}{3} \hspace{0.15cm}\underline{ \approx 0.943}.$$
(3) The equation of determination of the eigenvalues of $\mathbf{K_z}$ is:
- $${\rm det} \left[ \begin{array}{ccc} 1-\lambda & 1/3 & 1/3\\ 1/3 & 1-\lambda & 1/3\\ 1/3 & 1/3 & 1-\lambda \end{array}\right] = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}(1- \lambda) \left[(1- \lambda)^2 - \frac{1}{9} \right]- \frac{1}{3} \left[\frac{1}{3}(1- \lambda) - \frac{1}{9} \right] + \frac{1}{3} \left[\frac{1}{9} - \frac{1}{3}(1- \lambda) \right] = 0$$
- $$\Rightarrow \hspace{0.3cm}(1- \lambda) (\lambda^2 -2\lambda+ \frac{8}{9})- \frac{1}{9} (\frac{2}{3}- \lambda )+ \frac{1}{9} ( \lambda - \frac{2}{3})= 0$$
- $$\Rightarrow \hspace{0.3cm}\lambda^2 - 2\lambda + \frac{8}{9} - \lambda^3 + 2 \lambda^2 - \frac{8}{9}\lambda - \frac{4}{27} + \frac{2}{9}\lambda = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\lambda^3 - 3 \lambda^2 + \frac{24}{9}\lambda - \frac{20}{27} = 0.$$
- This equation has already been given as a solution hint, as well as one of the solutions: $\lambda_1= 5/3$.
- This gives the equation of determination for the further eigenvalues $\lambda_2$ and $\lambda_3$ to.
- $$\frac{\lambda^3 - 3 \lambda^2 + {24}/{9}\lambda - {20}/{27}}{\lambda -{5}/{3}} = \lambda^2 - {4}/{3} \cdot \lambda + {4}/{9} =0.$$
- This equation of determination can be transformed as follows: $(\lambda - {2}/{3})^2 =0.$
- The other eigenvalues besides $\lambda_1= 5/3$ are thus equal and result in $\lambda_2 = \lambda_3 =2/3\hspace{0.15cm}\underline{=0.667}$.
(4) Analogous to the procedure in the subtask (2) results here:
- $${N_3\hspace{0.01cm}'}/{N_3} = \sqrt{\lambda_1 \cdot \lambda_2\cdot \lambda_3} = \sqrt{\frac{5}{3} \cdot \frac{2}{3}\cdot \frac{2}{3}} = \sqrt{\frac{20}{27}} \hspace{0.15cm}\underline{ \approx 0.861}.$$