Difference between revisions of "Aufgaben:Exercise 3.11: Viterbi Receiver and Trellis Diagram"
| Line 33: | Line 33: | ||
- The noise power is only affected by $H_{\rm MF}(f)$, not by $H_{\rm DF}(f)$. | - The noise power is only affected by $H_{\rm MF}(f)$, not by $H_{\rm DF}(f)$. | ||
| − | { | + | {At what times $\nu$ can we finally decide the current symbol $a_{\rm \nu}$? |
|type="[]"} | |type="[]"} | ||
+ $\nu = 1,$ | + $\nu = 1,$ | ||
| Line 41: | Line 41: | ||
+ $\nu = 5.$ | + $\nu = 5.$ | ||
| − | { | + | {What is the sequence decided by the Viterbi receiver? |
|type="{}"} | |type="{}"} | ||
$a_1 \ = \ $ { 0. } | $a_1 \ = \ $ { 0. } | ||
| Line 49: | Line 49: | ||
$a_5 \ = \ $ { 0. } | $a_5 \ = \ $ { 0. } | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - It is certain that the detected sequence was also sent. |
| − | + | + | + A MAP receiver would have the same error probability. |
| − | - | + | - Threshold decision is the same as this maximum likelihood receiver. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The <u>first two solutions</u> are correct: |
| − | * | + | *The signal $m(t)$ after the matched filter $H_{\rm MF}(f)$ has the largest possible signal-to-interference power ratio. |
| − | * | + | * However, the noise components of the sequence $〈m_{\rm \nu}〉$ are (strongly) correlated due to the spectral shaping. |
| − | * | + | *The task of the discrete-time decorrelation filter with the frequency response $H_{\rm DF}(f)$ is to dissolve these bonds, which is why the name "whitening filter" is also used for $H_{\rm DF}(f)$. |
| − | * | + | *However, this is possible only at the cost of increased noise power ⇒ consequently, the last proposed solution does not apply. |
| − | '''(2)''' | + | '''(2)''' The two arrows arriving at $\underline {\nu = 1}$ are each drawn in blue and indicate the symbol $a_1 = 0$. Thus, the initial symbol $a_1$ is already fixed at this point. Similarly, the symbols $a_3 = 1$ and $a_5 = 0$ are already fixed at the timesn $\underline {\nu = 3}$ and $\underline {\nu = 5}$, respectively. |
| − | + | In contrast, at time $\nu = 2$, a decision regarding symbol $a_2$ is not possible. | |
| − | * | + | *Under the hypothesis that the following symbol $a_3 = 0$ would result in symbol $a_2 = 1$ (at "$0$" a red path arrives, thus coming from "$1$"). |
| − | * | + | * In contrast, the hypothesis $a_3 = 1$ leads to the result $a_2 = 0$ (the path arriving at "$1$" is blue). |
| − | + | The situation is similar at time $\nu = 4$. | |
| − | '''(3)''' | + | '''(3)''' From the continuous paths at $\nu = 5$ it can be seen: |
:$$a_{1}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} | :$$a_{1}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} | ||
a_{2}\hspace{0.15cm}\underline { =0} \hspace{0.05cm},\hspace{0.2cm}a_{3}\hspace{0.15cm}\underline {=1} | a_{2}\hspace{0.15cm}\underline { =0} \hspace{0.05cm},\hspace{0.2cm}a_{3}\hspace{0.15cm}\underline {=1} | ||
| Line 83: | Line 83: | ||
| − | '''(4)''' | + | '''(4)''' Only the <u>second statement</u> is correct: |
| − | * | + | *Since the source symbols "$0$" and "$1$" were assumed to be equally probable, the ML receiver (Viterbi) is identical to the MAP receiver. |
| − | * | + | *A threshold decision (which makes a symbol-by-symbol decision at each clock) has the same error probability as the Viterbi receiver only if there is no intersymbol interference. |
| − | * | + | *This is obviously not the case here, otherwise it should be possible to make a final decision at every time $\nu$. |
| − | * | + | *The first statement is also not true. Indeed, this would mean that the Viterbi receiver can have error probability $0$ in the presence of statistical noise. This is not possible for information-theoretic reasons. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 09:47, 8 June 2022
The Viterbi receiver allows a low-effort realization of the maximum likelihood decision rule. It contains the system components listed below:
- a matched filter adapted to the basic transmission pulse with frequency response $H_{\rm MF}(f)$ and output signal $m(t)$,
- a sampler spaced at the symbol duration (bit duration) $T$, which converts the continuous-time signal $m(t)$ into the discrete-time sequence $〈m_{\rm \nu}〉$,
- a decorrelation filter with frequency response $H_{\rm DF}(f)$ for removing statistical ties between the noise components of the sequence $〈d_{\rm \nu}〉$,
- the Viterbi decision, which uses a trellis-based algorithm to obtain the sink symbol sequence $〈v_{\rm \nu}〉$.
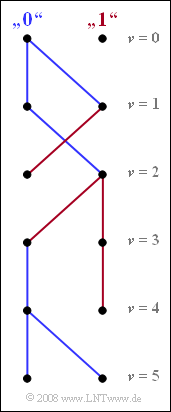
The graph shows the simplified trellis diagram of the two states "$0$" and "$1$" for time points $\nu ≤ 5$. This diagram is obtained as a result of evaluating the two minimum total error quantities ${\it \Gamma}_{\rm \nu}(0)$ and ${\it \Gamma}_{\rm \nu}(1)$ corresponding to "Exercise 3.11Z".
Notes:
- The exercise belongs to the chapter "Viterbi Receiver".
- Reference is also made to the section "MAP and Maximum–Likelihood decision rule".
- All quantities here are to be understood normalized. Also assume unipolar and equal probability amplitude coefficients: ${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$
- The topic is also covered in the interactive applet "Properties of the Viterbi Receiver".
Questions
Solution
- The signal $m(t)$ after the matched filter $H_{\rm MF}(f)$ has the largest possible signal-to-interference power ratio.
- However, the noise components of the sequence $〈m_{\rm \nu}〉$ are (strongly) correlated due to the spectral shaping.
- The task of the discrete-time decorrelation filter with the frequency response $H_{\rm DF}(f)$ is to dissolve these bonds, which is why the name "whitening filter" is also used for $H_{\rm DF}(f)$.
- However, this is possible only at the cost of increased noise power ⇒ consequently, the last proposed solution does not apply.
(2) The two arrows arriving at $\underline {\nu = 1}$ are each drawn in blue and indicate the symbol $a_1 = 0$. Thus, the initial symbol $a_1$ is already fixed at this point. Similarly, the symbols $a_3 = 1$ and $a_5 = 0$ are already fixed at the timesn $\underline {\nu = 3}$ and $\underline {\nu = 5}$, respectively.
In contrast, at time $\nu = 2$, a decision regarding symbol $a_2$ is not possible.
- Under the hypothesis that the following symbol $a_3 = 0$ would result in symbol $a_2 = 1$ (at "$0$" a red path arrives, thus coming from "$1$").
- In contrast, the hypothesis $a_3 = 1$ leads to the result $a_2 = 0$ (the path arriving at "$1$" is blue).
The situation is similar at time $\nu = 4$.
(3) From the continuous paths at $\nu = 5$ it can be seen:
- $$a_{1}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} a_{2}\hspace{0.15cm}\underline { =0} \hspace{0.05cm},\hspace{0.2cm}a_{3}\hspace{0.15cm}\underline {=1} \hspace{0.05cm},\hspace{0.2cm} a_{4}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} a_{5}\hspace{0.15cm}\underline {=0} \hspace{0.05cm}.$$
(4) Only the second statement is correct:
- Since the source symbols "$0$" and "$1$" were assumed to be equally probable, the ML receiver (Viterbi) is identical to the MAP receiver.
- A threshold decision (which makes a symbol-by-symbol decision at each clock) has the same error probability as the Viterbi receiver only if there is no intersymbol interference.
- This is obviously not the case here, otherwise it should be possible to make a final decision at every time $\nu$.
- The first statement is also not true. Indeed, this would mean that the Viterbi receiver can have error probability $0$ in the presence of statistical noise. This is not possible for information-theoretic reasons.