Difference between revisions of "Aufgaben:Exercise 4.06Z: Signal Space Constellations"
| Line 3: | Line 3: | ||
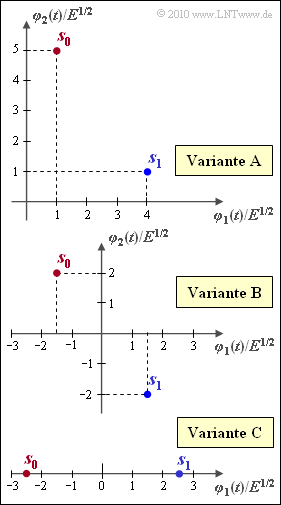
[[File:P_ID2016__Dig_Z_4_6.png|right|frame|Three signal space constellations]] | [[File:P_ID2016__Dig_Z_4_6.png|right|frame|Three signal space constellations]] | ||
| − | + | The (mean) error probability of an optimal binary system is: | |
:$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )\hspace{0.05cm}.$$ | :$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )\hspace{0.05cm}.$$ | ||
| − | + | It should be noted here: | |
| − | * ${\rm Q}(x)$ | + | * ${\rm Q}(x)$ denotes the complementary Gaussian error function (definition and approximation): |
:$${\rm Q}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u | :$${\rm Q}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u | ||
\approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} | \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * $d$ | + | * $d$ specifies the distance between the two transmitted signal points $s_0$ and $s_1$ in vector space: |
:$$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} \hspace{0.05cm}.$$ | :$$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} \hspace{0.05cm}.$$ | ||
| − | * $\sigma_n^2$ | + | * $\sigma_n^2$ is the variance of the AWGN noise after the detector, which, for example, can be implemented as a matched filter. <br>It is assumed that $\sigma_n^2 = N_0/2$. |
| − | + | The graphic shows three different signal space constellations, namely | |
| − | * | + | * Variant $\rm A$: $s_0 = (+1, \, +5), \hspace{0.4cm} s_1 = (+4, \, +1)$, |
| − | * | + | * Variant $\rm B$: $s_0 = (-1.5, \, +2), \, s_1 = (+1.5, \, -2)$, |
| − | * | + | * Variant $\rm C$: $s_0 = (-2.5, \, 0), \hspace{0.45cm} s_1 = (+2.5, \, 0)$. |
| − | + | The mean energy per symbol $(E_{\rm S})$ can be calculated as follows: | |
:$$E_{\rm S} = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot || \boldsymbol{ s }_0||^2 + | :$$E_{\rm S} = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot || \boldsymbol{ s }_0||^2 + | ||
{\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot || \boldsymbol{ s }_1||^2\hspace{0.05cm}.$$ | {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot || \boldsymbol{ s }_1||^2\hspace{0.05cm}.$$ | ||
| Line 34: | Line 34: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | * The chapter belongs to the chapter [[Digital_Signal_Transmission/Approximation_of_the_Error_Probability|"Approximation of the Error Probability"]]. |
| − | * | + | * For numeric calculations, the energy $E = 1$ can be set for simplification. |
| − | * | + | * Unless otherwise specified, equally probable symbols can be assumed: |
:$${\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) = 0.5\hspace{0.05cm}.$$ | :$${\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) = 0.5\hspace{0.05cm}.$$ | ||
| Line 44: | Line 44: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which prerequisites must absolutely (in any case) be fulfilled so that the given error probability equation is valid? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Additive white Gaussian noise with variance $\sigma_n^2$. |
| − | + | + | + Optimal binary receiver. |
| − | + | + | + Decision boundary in the middle between the symbols. |
| − | - | + | - Equally likely symbols $s_0$ and $s_1$. |
| − | { | + | {Which statement applies to the error probability with $\sigma_n^2 = E$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Variant $\rm A$ has the lowest error probability. |
| − | - | + | - Variant $\rm B$ has the lowest error probability. |
| − | - | + | - Variant $\rm C$ has the lowest error probability. |
| − | + | + | + All variants show the same error behavior. |
| − | { | + | {Give the error probability for variant $\rm A$ with $\sigma_n^2 = E$. You can calculate ${\rm Q}(x)$ according to the approximation. |
|type="{}"} | |type="{}"} | ||
$p_{\rm S} \ = \ $ { 0.7 3% } $\ \%$ | $p_{\rm S} \ = \ $ { 0.7 3% } $\ \%$ | ||
| − | { | + | {It is assumed that $N_0 = 2 \cdot 10^{\rm –6} \ {\rm W/Hz}$, $E_{\rm S} = 6.25 \cdot 10^{\rm –6} \ \rm Ws$. What is the probability for variant $\rm C$ with equally probable symbols? |
|type="{}"} | |type="{}"} | ||
$p_{\rm S} \ = \ $ { 0.7 3% } $\ \%$ | $p_{\rm S} \ = \ $ { 0.7 3% } $\ \%$ | ||
| − | { | + | {What is the error probability for variant $\rm B$ under the same conditions? |
|type="{}"} | |type="{}"} | ||
$p_{\rm S} \ = \ $ { 0.7 3% } $\ \%$ | $p_{\rm S} \ = \ $ { 0.7 3% } $\ \%$ | ||
| − | { | + | {How large should the average energy per symbol $(E_{\rm S})$ be chosen for variant $\rm A$ in order to obtain the same error probability as for system $\rm C$? |
|type="{}"} | |type="{}"} | ||
$E_{\rm S} \ = \ $ { 21.5 3% } $\ \cdot 10^{\rm –6} \ \rm Ws$ | $E_{\rm S} \ = \ $ { 21.5 3% } $\ \cdot 10^{\rm –6} \ \rm Ws$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The <u>first three prerequisites</u> must be met in any case: |
| − | * | + | *The equation then applies independently of the occurrence probabilities. |
| − | * | + | *In the case of ${\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_0) ≠ {\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_1)$, a lower error probability can be achieved by shifting the decision threshold. |
| − | '''(2)''' | + | '''(2)''' The noise rms value $\sigma_n$ and thus also the signal energy $E = \sigma_n^2$ are the same for all three considered variants. The same applies to the distance of the signal space points. For variant $\rm A$, for example, the following applies: |
:$$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} = \sqrt{ E \cdot (4-1)^2 + E \cdot (1-5)^2} = 5 \cdot \sqrt{E}\hspace{0.05cm}.$$ | :$$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} = \sqrt{ E \cdot (4-1)^2 + E \cdot (1-5)^2} = 5 \cdot \sqrt{E}\hspace{0.05cm}.$$ | ||
| − | + | Due to the shifting of the coordinate system, the distance between $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$ does not change (variant $\rm B$), and the same distance results in variant $\rm C$ (after rotation). | |
| − | + | <u>Solution 4</u> is correct: | |
*Durch eine Drehung des Koordinatensystems kann man bei einem Binärsystem $(M = 2)$ stets mit einer Basisfunktion $(N = 1)$ auskommen. | *Durch eine Drehung des Koordinatensystems kann man bei einem Binärsystem $(M = 2)$ stets mit einer Basisfunktion $(N = 1)$ auskommen. | ||
*Da das zweidimensionale Rauschen zirkulär symmetrisch ist ⇒ gleiche Streuung $\sigma_n$ in alle Richtungen, kann auch der Rauschterm wie im Kapitel [[Digitalsignal%C3%BCbertragung/Fehlerwahrscheinlichkeit_bei_Basisband%C3%BCbertragung|Fehlerwahrscheinlichkeit bei Basisbandübertragung]] eindimensional beschrieben werden. | *Da das zweidimensionale Rauschen zirkulär symmetrisch ist ⇒ gleiche Streuung $\sigma_n$ in alle Richtungen, kann auch der Rauschterm wie im Kapitel [[Digitalsignal%C3%BCbertragung/Fehlerwahrscheinlichkeit_bei_Basisband%C3%BCbertragung|Fehlerwahrscheinlichkeit bei Basisbandübertragung]] eindimensional beschrieben werden. | ||
Revision as of 14:39, 5 July 2022
The (mean) error probability of an optimal binary system is:
- $$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )\hspace{0.05cm}.$$
It should be noted here:
- ${\rm Q}(x)$ denotes the complementary Gaussian error function (definition and approximation):
- $${\rm Q}(x) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u \approx \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$
- $d$ specifies the distance between the two transmitted signal points $s_0$ and $s_1$ in vector space:
- $$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} \hspace{0.05cm}.$$
- $\sigma_n^2$ is the variance of the AWGN noise after the detector, which, for example, can be implemented as a matched filter.
It is assumed that $\sigma_n^2 = N_0/2$.
The graphic shows three different signal space constellations, namely
- Variant $\rm A$: $s_0 = (+1, \, +5), \hspace{0.4cm} s_1 = (+4, \, +1)$,
- Variant $\rm B$: $s_0 = (-1.5, \, +2), \, s_1 = (+1.5, \, -2)$,
- Variant $\rm C$: $s_0 = (-2.5, \, 0), \hspace{0.45cm} s_1 = (+2.5, \, 0)$.
The mean energy per symbol $(E_{\rm S})$ can be calculated as follows:
- $$E_{\rm S} = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot || \boldsymbol{ s }_0||^2 + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot || \boldsymbol{ s }_1||^2\hspace{0.05cm}.$$
Notes:
- The chapter belongs to the chapter "Approximation of the Error Probability".
- For numeric calculations, the energy $E = 1$ can be set for simplification.
- Unless otherwise specified, equally probable symbols can be assumed:
- $${\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) = {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) = 0.5\hspace{0.05cm}.$$
Questions
Solution
- The equation then applies independently of the occurrence probabilities.
- In the case of ${\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_0) ≠ {\rm Pr}(\boldsymbol{s} = \boldsymbol{s}_1)$, a lower error probability can be achieved by shifting the decision threshold.
(2) The noise rms value $\sigma_n$ and thus also the signal energy $E = \sigma_n^2$ are the same for all three considered variants. The same applies to the distance of the signal space points. For variant $\rm A$, for example, the following applies:
- $$d = \sqrt{ || \boldsymbol{ s }_1 - \boldsymbol{ s }_0||^2} = \sqrt{ E \cdot (4-1)^2 + E \cdot (1-5)^2} = 5 \cdot \sqrt{E}\hspace{0.05cm}.$$
Due to the shifting of the coordinate system, the distance between $\boldsymbol{s}_0$ and $\boldsymbol{s}_1$ does not change (variant $\rm B$), and the same distance results in variant $\rm C$ (after rotation).
Solution 4 is correct:
- Durch eine Drehung des Koordinatensystems kann man bei einem Binärsystem $(M = 2)$ stets mit einer Basisfunktion $(N = 1)$ auskommen.
- Da das zweidimensionale Rauschen zirkulär symmetrisch ist ⇒ gleiche Streuung $\sigma_n$ in alle Richtungen, kann auch der Rauschterm wie im Kapitel Fehlerwahrscheinlichkeit bei Basisbandübertragung eindimensional beschrieben werden.
(3) Für alle hier betrachteten Varianten gilt, also auch für die Variante $\rm A$:
- $$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right )= {\rm Q} \left ( \frac{5/2 \cdot \sqrt{E}}{\sigma_n} \right ) = {\rm Q}(2.5)\hspace{0.05cm}.$$
Mit der angegebenen Näherung erhält man
- $$p_{\rm S} = \frac{1}{\sqrt{2\pi} \cdot 2.5} \cdot {\rm e}^{-2.5^2/2} \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.7 \%}\hspace{0.05cm}.$$
(4) Bei der Variante $\rm C$ ergibt sich für die mittlere Energie pro Symbol:
- $$E_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \cdot (-2.5 \cdot \sqrt{E})^2 + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_1) \cdot (+ 2.5 \cdot \sqrt{E})^2 = \left [ {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) + {\rm Pr}(\boldsymbol{ s } = \boldsymbol{ s }_0) \right ] \cdot 6.25 \cdot E = 6.25 \cdot E$$
- $$\Rightarrow \hspace{0.3cm} E = \frac {E_{\rm S}}{6.25} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sqrt{E}= \frac {\sqrt{E_{\rm S}}}{2.5} \hspace{0.05cm}.$$
Setzt man dieses Ergebnis in die unter (3) gefundene Gleichung ein, so erhält man mit $\sigma_n^2 = N_0/2$:
- $$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Q} \left ( \frac{2.5 \cdot \sqrt{E}}{\sigma_n} \right )= {\rm Q} \left ( \frac{ \sqrt{E_{\rm S}}}{\sigma_n} \right ) = {\rm Q} \left ( \frac{ \sqrt{2 \cdot E_{\rm S}}}{N_0} \right ) ={\rm Q} \left ( \sqrt{\frac{ 2 \cdot 6.25 \cdot 10^{-6}\,{\rm Ws}}{2 \cdot 10^{-6}\,{\rm W/Hz}}} \right ) ={\rm Q}(2.5) \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.7 \%}\hspace{0.05cm}. $$
(5) Durch Drehung des Koordinatensystems ändert sich nichts an den Energieverhältnissen. Deshalb erhält man wieder $p_{\rm S} \ \underline {\approx 0.7\%}$.
(6) Bei der Variante $\rm A$ ist die mittlere Energie pro Symbol
- $$E_{\rm S} = {1}/{2} \cdot \left [ (1^2 + 5^2) \cdot E + (4^2 + 1^2) \cdot E \right ] = 21.5 \cdot E \hspace{0.05cm}. $$
Der Abstand von der Schwelle, die bei gleichwahrscheinlichen Symbolen in der Mitte zwischen $\boldsymbol{s}_0$ und $\boldsymbol{s}_1$ liegen sollte, ist wie bei den anderen Varianten $d/2 = 2.5 \cdot E^{\rm 1/2}$. Mit $\sigma_n^2 = N_0/2$ erhält man somit die Bestimmungsgleichung:
- $$p_{\rm S} = {\rm Q} \left ( \frac{ 2.5 \cdot \sqrt{E}}{\sqrt{N_0/2}} \right ) ={\rm Q}(2.5)\approx 0.7 \cdot 10^{-2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sqrt{\frac {2E}{N_0}} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac {E}{N_0} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\frac {E_{\rm S}}{21.5 \cdot N_0} = 0.5$$
- $$\Rightarrow \hspace{0.3cm} {E_{\rm S}} = 0.5 \cdot {21.5 \cdot N_0} \hspace{0.1cm} \hspace{0.15cm}\underline { = 21.5 \cdot 10^{-6}\,{\rm Ws}}\hspace{0.05cm}.$$
Das bedeutet: Bei der Variante $\rm A$ ist gegenüber den beiden anderen Symbolen eine um den Faktor $3.44$ größere mittlere Symbolenergie $E_{\rm S}$ erforderlich, um die gleiche Fehlerwahrscheinlichkeit $p_{\rm S} = 0.7%$ zu erzielen.
- Das heißt: Diese Signalraumkonstellation ist sehr ungünstig. Es ergibt sich ein sehr großes $E_{\rm S}$, ohne dass gleichzeitig der Abstand $d$ vergrößert wird.
- Mit $E_{\rm S} = 6.25 \cdot 10^{\rm –6} \ \rm Ws$ würde sich dagegen $p_{\rm S} = {\rm Q}(2.5/3.44^{\rm 1/2}) \approx {\rm Q}(1.35) \approx 9\%$ ergeben.
- Das heißt: Die Fehlerwahrscheinlichkeit würde um mehr als eine Zehnerpotenz größer.