Aufgaben:Exercise 4.4: Maximum–a–posteriori and Maximum–Likelihood

• Return to book

Channel transition probabilities

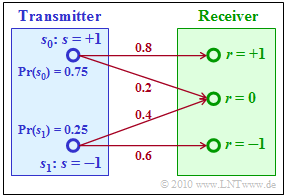
To illustrate  "maximum–a–posteriori"  $\rm (MAP)$  and  "maximum likelihood"  $\rm (ML)$  decision,  we now construct a very simple example with only two possible messages  $m_0 = 0$  and  $m_1 = 1$,  represented by the signal values  $s_0$  resp.  $s_1$:

$$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_0 = +1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_0 = 0\hspace{0.05cm},$$

$$s \hspace{-0.15cm} \ = \ \hspace{-0.15cm}s_1 = -1 \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm}m = m_1 = 1\hspace{0.05cm}.$$

• Let the probabilities of occurrence be:

$${\rm Pr}(s = s_0) = 0.75,\hspace{0.2cm}{\rm Pr}(s = s_1) = 0.25 \hspace{0.05cm}.$$

• The received signal can – for whatever reason – take three different values, i.e.

$$r = +1,\hspace{0.2cm}r = 0,\hspace{0.2cm}r = -1 \hspace{0.05cm}.$$

• The conditional channel probabilities can be taken from the graph.

After transmission, the message is to be estimated by an optimal receiver.  Available are:

• the  maximum likelihood receiver  $\rm (ML$  receiver$)$,  which does not know the occurrence probabilities  ${\rm Pr}(s = s_i)$,  with the decision rule:

$$\hat{m}_{\rm ML} = {\rm arg} \max_i \hspace{0.1cm} \big[ p_{r |s } \hspace{0.05cm} (\rho |s_i ) \big]\hspace{0.05cm},$$

• the  maximum-a-posteriori receiver$\rm (MAP$  receiver$)$;  this receiver also considers the symbol probabilities of the source in its decision process:

$$\hat{m}_{\rm MAP} = {\rm arg} \max_i \hspace{0.1cm} \big[ {\rm Pr}( s = s_i) \cdot p_{r |s } \hspace{0.05cm} (\rho |s_i ) \big ]\hspace{0.05cm}.$$

Notes:

• The exercise belongs to the chapter  "Optimal Receiver Strategies".

• Reference is also made to the chapter  "Structure of the Optimal Receiver.

• The necessary statistical principles can be found in the chapter  "Statistical Dependence and Independence"  of the book  "Theory of Stochastic Signals".

Questions

1

With which probabilities do the received values occur?

${\rm Pr}(r = +1) \ = \ $

${\rm Pr}(r = -1) \ = \ $

${\rm Pr}(r = 0) \hspace{0.45cm} = \ $

2

Calculate all inference probabilities.

${\rm Pr}(s_0|r = +1) \ = \ $

${\rm Pr}(s_1|r = +1) \ = \ $

${\rm Pr}(s_0|r = -1) \ = \ $

${\rm Pr}(s_1|r = -1) \ = \ $

${\rm Pr}(s_0|r = 0) \hspace{0.45cm} = \ $

${\rm Pr}(s_1|r = 0) \hspace{0.45cm} = \ $

3

Do MAP and ML receivers differ under the condition  "$r = +1$"?

	yes,
	no.

4

Do MAP and ML receivers differ under the condition  "$r = -1$"?

	yes,
	no.

5

Which statements are true under the condition  "$r = 0$"?

	The MAP receiver decides for  $s_0$.
	The MAP receiver decides for  $s_1$.
	The ML receiver decides for  $s_0$.
	The ML receiver decides for  $s_1$.

6

Calculate the symbol error probability of the  ML receiver.

${\rm Pr(symbol\hspace{0.15cm} error)}\ = \ $

7

Calculate the symbol error probability of the  MAP receiver.

${\rm Pr(symbol\hspace{0.15cm}error)}\ = \ $

Solution

Solution

(1)  The receiver side occurrence probabilities we are looking for are

$${\rm Pr} ( r = +1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} ( s_0) \cdot {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s = +1) = 0.75 \cdot 0.8 \hspace{0.05cm}\hspace{0.15cm}\underline { = 0.6}\hspace{0.05cm},$$

$${\rm Pr} ( r = -1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm Pr} ( s_1) \cdot {\rm Pr} ( r = -1 \hspace{0.05cm}| \hspace{0.05cm}s = -1) = 0.25 \cdot 0.6 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15}\hspace{0.05cm},$$

$${\rm Pr} ( r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 - {\rm Pr} ( r = +1) - {\rm Pr} ( r = -1) = 1 - 0.6 - 0.15 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm}.$$

For the last probability also holds:

$${\rm Pr} ( r = 0) = 0.75 \cdot 0.2 + 0.25 \cdot 0.4 = 0.25\hspace{0.05cm}.$$

(2)  For the first inference probability we are looking for holds:

$${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = \frac{{\rm Pr} ( r = +1 \hspace{0.05cm}|\hspace{0.05cm}s_0 ) \cdot {\rm Pr} ( s_0)}{{\rm Pr} ( r = +1)} = \frac{0.8 \cdot 0.75}{0.6} \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$

Correspondingly, we obtain for the other probabilities:

$${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{-0.1cm} \ = \ 1 - {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$

$${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$

$${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = -1) \hspace{0.05cm}\hspace{0.15cm}\underline {= 1}\hspace{0.05cm},$$

$${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm}\frac{{\rm Pr} ( r = 0 \hspace{0.05cm}|\hspace{0.05cm}s_0 ) \cdot {\rm Pr} ( s_0)}{{\rm Pr} ( r = 0 )}= \frac{0.2 \cdot 0.75}{0.25} \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.6}\hspace{0.05cm},$$

$${\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1- {\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.4} \hspace{0.05cm}.$$

(3)  Let $r = +1$. Then decides

• the MAP receiver for $s_0$, because ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = +1) = 1 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = +1)= 0\hspace{0.05cm},$
• the ML receiver likewise for $s_0$, since ${\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.8 > {\rm Pr} ( r = +1 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0 \hspace{0.05cm}.$

So the correct answer is NO.

(4)  NO is also true under the condition "$r = \, –1$", since there is no connection between $s_0$ and "$r = \, –1$".

(5)  Solutions 1 and 4 are correct:

• The MAP receiver will choose event $s_0$, since ${\rm Pr} (s_0 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.6 > {\rm Pr} (s_1 \hspace{0.05cm}| \hspace{0.05cm}r = 0) = 0.4 \hspace{0.05cm}.$
• In contrast, the ML receiver will choose $s_1$, since ${\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_1) = 0.4 > {\rm Pr} ( r = 0 \hspace{0.05cm}| \hspace{0.05cm}s_0) = 0.2 \hspace{0.05cm}.$

(6)  The maximum likelihood receiver

• decides for $s_0$ only if $r = +1$,
• thus makes no error if $s_1$ was sent,
• only makes an error when "$s_0$" and "$r = 0$" are combined:

$${\rm Pr} ({\rm symbol error} ) = {\rm Pr} ({\cal E } ) = 0.75 \cdot 0.2 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.15} \hspace{0.05cm}.$$

(7)  The MAP receiver, on the other hand, decides to use $s_0$ when "$r = 0$". So there is a symbol error only in the combination "$s_1$" and "$r = 0$". From this follows:

$${\rm Pr} ({\rm symbol error} ) = {\rm Pr} ({\cal E } ) = 0.25 \cdot 0.4 \hspace{0.05cm}\hspace{0.15cm}\underline {= 0.1} \hspace{0.05cm}.$$

• The error probability here is lower than for the ML receiver,
• because now also the different apriori probabilities ${\rm Pr}(s_0)$ and ${\rm Pr}(s_1)$ are considered.