Aufgaben:Exercise 5.2: Error Correlation Function

• Return to book

Probabilities of error distances and ECF

For the characterization of digital channel models one uses among other things

• the error correlation function (ECF)

$$\varphi_{e}(k) = {\rm E}\big[e_{\nu} \cdot e_{\nu + k}\big]\hspace{0.05cm}, \hspace{0.2cm} k \ge 0\hspace{0.05cm},$$

• the error distance probabilities

$${\rm Pr}( a =k) \hspace{0.05cm}, \hspace{0.2cm} k \ge 1\hspace{0.05cm}.$$

Here denote:

• $〈e_{\rm \nu}〉$  is the error sequence with  $e_{\rm \nu} ∈ \{0, 1\}$.
• $a$  indicates the error distance.

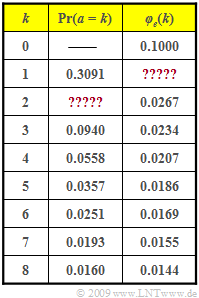
Two directly consecutive bit errors are thus characterized by the error distance  $a = 1$. 

The table shows exemplary values of the error distance probabilities  ${\rm Pr}(a = k)$  as well as the error correlation function  $\varphi_e(k)$.

• Some data are missing in the table.
• These values are to be calculated from the given values.

Note:

• The exercise covers the subject matter of the chapter  "Parameters of Digital Channel Models".

Questions

1

Which value results for the average error probability?

$p_{\rm M} \ = \ $

2

Which value results for the mean error distance?

${\rm E}\big[a\big] \ = \ $

3

Calculate the value of the error correlation function (ECF) for  $k = 1$.

$\varphi_e(k = 1) \ = \ $

4

What is the approximation for the probability of the error distance  $a = 2$?

${\rm Pr}(a = 2) \ = \ $

Solution

Solution

(1)  The mean probability of error is equal to the ECF value for $k = 0$. Namely, because of $e_{\nu} ∈ \{0, 1\}$:

$$\varphi_{e}(k = 0) = {\rm E}[e_{\nu}^2 ]= {\rm E}[e_{\nu} ]= p_{\rm M} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm M}\hspace{0.15cm}\underline { = 0.1} \hspace{0.05cm}.$$

(2)  The mean error distance is equal to the reciprocal of the mean error probability. That is:

$${\rm E}\big[a\big] = 1/p_{\rm M} \ \underline {= 10}.$$

(3)  According to the definition equation and "Bayes' theorem", the following result is obtained:

$$\varphi_{e}(k = 1) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm E}[e_{\nu} \cdot e_{\nu + 1}] = {\rm E}[(e_{\nu} = 1) \cdot (e_{\nu + 1}=1)]={\rm Pr}(e_{\nu + 1}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot {\rm Pr}(e_{\nu} = 1) \hspace{0.05cm}.$$

• The first probability is equal to ${\rm Pr}(a = 1)$ and the second probability is equal to $p_{\rm M}$:

$$\varphi_{e}(k = 1) = 0.3091 \cdot 0.1\hspace{0.15cm}\underline { = 0.0309} \hspace{0.05cm}.$$

(4)  The ECF value $\varphi_e(k = 2)$ can be interpreted (approximately) as follows:

$$\varphi_{e}(k = 2) ={\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) \cdot p_{\rm M} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = \frac{\varphi_{e}(k = 2)}{p_{\rm M}} = \frac{0.0267}{0.1} = 0.267\hspace{0.05cm}.$$

This probability is composed of  "At time $\nu+1$ an error occurs"  and  "At time $\nu+1$ there is no error":

$${\rm Pr}(e_{\nu + 2}=1 \hspace{0.05cm}|\hspace{0.05cm} e_{\nu} = 1) = {\rm Pr}( a =1) \cdot {\rm Pr}( a =1) + {\rm Pr}( a =2)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}( a =2)= 0.267 - 0.3091^2 \hspace{0.15cm}\underline {= 0.1715}\hspace{0.05cm}.$$

In the calculation, it was assumed that the individual error distances are statistically independent of each other.

• However, this assumption is valid only for a special class of channel models called "renewing".
• The bundle fault model considered here does not satisfy this condition.
• The actual probability  ${\rm Pr}(a = 2) = 0.1675$  therefore deviates slightly from the value calculated here  $(0.1715)$.