Difference between revisions of "Aufgaben:Exercise 4.19: Orthogonal Multilevel FSK"
| Line 69: | Line 69: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
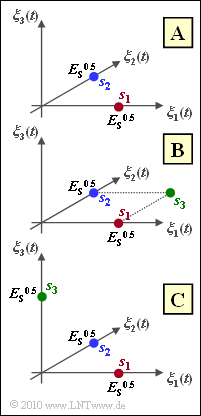
| − | '''(1)''' <u>Solutions 1 and 3</u> are correct: | + | '''(1)''' <u>Solutions 1 and 3</u> are correct: |
| − | *In constellation $\rm B$ the orthogonality is not given. Rather $M = 3$ and $N = 2$ are valid here. | + | *In constellation $\rm B$ the orthogonality is not given. Rather $M = 3$ and $N = 2$ are valid here. |
| − | '''(2)''' For the binary FSK $(M = 2)$ applies with the abbreviation $x = E_{\rm S}/N_0 = 6$: | + | '''(2)''' For the binary FSK $(M = 2)$ applies with the abbreviation $x = E_{\rm S}/N_0 = 6$: |
:$$p_{\rm S} = (-1)^{2} \cdot {1 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-x/2 } = {1}/{2} \cdot {\rm e }^{-3} \hspace{0.15cm}\underline{\approx 2.49 \%} | :$$p_{\rm S} = (-1)^{2} \cdot {1 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-x/2 } = {1}/{2} \cdot {\rm e }^{-3} \hspace{0.15cm}\underline{\approx 2.49 \%} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Accordingly, for the ternary FSK $(M = 3)$ we obtain: | + | *Accordingly, for the ternary FSK $(M = 3)$ we obtain: |
:$$p_{\rm S} = (-1)^{2} \cdot {2 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-(1/2) \hspace{0.05cm} \cdot \hspace{0.05cm} x} + | :$$p_{\rm S} = (-1)^{2} \cdot {2 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-(1/2) \hspace{0.05cm} \cdot \hspace{0.05cm} x} + | ||
(-1)^{3} \cdot {2 \choose 2 } \cdot {1}/{3}\cdot {\rm e }^{-(2/3) \hspace{0.05cm} \cdot \hspace{0.05cm} x}= | (-1)^{3} \cdot {2 \choose 2 } \cdot {1}/{3}\cdot {\rm e }^{-(2/3) \hspace{0.05cm} \cdot \hspace{0.05cm} x}= | ||
| Line 84: | Line 84: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Finally, for the quaternary FSK $(M = 4)$ we obtain: | + | *Finally, for the quaternary FSK $(M = 4)$ we obtain: |
:$$p_{\rm S} = (-1)^{2} \cdot {3 \choose 1 } \cdot \frac{{\rm e }^{-x/2}}{2} + | :$$p_{\rm S} = (-1)^{2} \cdot {3 \choose 1 } \cdot \frac{{\rm e }^{-x/2}}{2} + | ||
(-1)^{3} \cdot {3 \choose 2 } \cdot \frac{{\rm e }^{-2x/3}}{3} | (-1)^{3} \cdot {3 \choose 2 } \cdot \frac{{\rm e }^{-2x/3}}{3} | ||
| Line 93: | Line 93: | ||
| − | '''(3)''' For equal $E_{\rm S}/N_0 = 6$, $p_{\rm S, \ max} ≥ p_{\rm S}$ always holds: | + | '''(3)''' For equal $E_{\rm S}/N_0 = 6$, $p_{\rm S, \ max} ≥ p_{\rm S}$ always holds: |
:$$M =2\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=2.49\%} = p_{\rm S} \hspace{0.05cm},$$ | :$$M =2\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=2.49\%} = p_{\rm S} \hspace{0.05cm},$$ | ||
:$$M =3\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=4.98\%} > 4.37\% = p_{\rm S} \hspace{0.05cm},$$ | :$$M =3\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=4.98\%} > 4.37\% = p_{\rm S} \hspace{0.05cm},$$ | ||
:$$M =4\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=7.47\%} > {6.75\%} = p_{\rm S} \hspace{0.05cm}.$$ | :$$M =4\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=7.47\%} > {6.75\%} = p_{\rm S} \hspace{0.05cm}.$$ | ||
| − | Analyzing the equation $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ in more detail, we see that this bound exactly specifies the [[Digital_Signal_Transmission/Approximation_of_the_Error_Probability#Union_Bound_-_Upper_bound_for_the_error_probability| "Union Bound"]]: | + | Analyzing the equation $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ in more detail, we see that this bound exactly specifies the [[Digital_Signal_Transmission/Approximation_of_the_Error_Probability#Union_Bound_-_Upper_bound_for_the_error_probability| "Union Bound"]]: |
| − | * For the binary system, $1/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ gives the falsification probability, for example from $\boldsymbol{s}_1$ to $\boldsymbol{s}_2$ or vice versa. | + | * For the binary system, $1/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ gives the falsification probability, for example from $\boldsymbol{s}_1$ to $\boldsymbol{s}_2$ or vice versa. |
| − | * For the | + | |
| − | * The "Union Bound" considers the distortion possibilities of a point to each of the generally $M–1$ other points by the factor $M -1$. | + | * For the $M$–level system, the distance between $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$ is exactly the same. But also the points $\boldsymbol{s}_3, \ \text{... ,} \, \boldsymbol{s}_M$ are at the same distance from $\boldsymbol{s}_1$ or from $\boldsymbol{s}_2$. |
| + | |||
| + | * The "Union Bound" considers the distortion possibilities of a point to each of the generally $M–1$ other points by the factor $M -1$. | ||
| + | |||
'''(4)''' With $E_{\rm B} = E_{\rm S}/{\rm log}_2(M)$ one obtains $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-\log_2 \ (M) E_{\rm B}/(2N_{\rm 0})}$. | '''(4)''' With $E_{\rm B} = E_{\rm S}/{\rm log}_2(M)$ one obtains $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-\log_2 \ (M) E_{\rm B}/(2N_{\rm 0})}$. | ||
| − | *The error probability becomes smaller as the number | + | *The error probability becomes smaller as the level-number increases, because at constant $E_{\rm B}$ the energy $E_{\rm S}$ per symbol increases by the factor ${\rm log}_2 \, (M)$. |
| − | *The factor $M-1$ (considers the falsification possibilities of a signal space point) has less influence than the increase of the negative exponent: | + | |
| + | *The factor $M-1$ (considers the falsification possibilities of a signal space point) has less influence than the increase of the negative exponent: | ||
:$$M =2\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{ 2} \cdot {\rm e }^{-3} \hspace{0.15cm} \underline{= 2.49\%} \hspace{0.05cm},$$ | :$$M =2\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{ 2} \cdot {\rm e }^{-3} \hspace{0.15cm} \underline{= 2.49\%} \hspace{0.05cm},$$ | ||
:$$M =3\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm e }^{-4.755} \hspace{0.5cm} \underline{= 0.86\%} \hspace{0.05cm},$$ | :$$M =3\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm e }^{-4.755} \hspace{0.5cm} \underline{= 0.86\%} \hspace{0.05cm},$$ | ||
Revision as of 13:13, 31 August 2022
In this last exercise of this chapter we consider "Frequency Shift Keying" $\rm (FSK)$ with $M$ waveforms and assume that they are orthogonal to each other in pairs.
- In this case, the equivalent low–pass signals $s_i(t)$ with $i = 1, \ \text{...} \ , M$ can be represented in the following form:
- $$s_i(t) = \sqrt{E_{\rm S}} \cdot \xi_i(t) \hspace{0.05cm}.$$
- $\xi_i(t)$ are complex basis functions for which in general $i = 1, \ \text{...} \ , N$. However, for orthogonal signaling, $M = N$ is always true.
- The diagram shows three different signal space constellations. However, not all three describe an orthogonal FSK. This is referred to in the subtask (1).
In the "theory part", the exact formula for the probability of a correct decision in the case of AWGN noise is given:
- $${\rm Pr}({\cal{C}}) =\sum_{i = 0}^{M-1} (-1)^i \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm e }^{ - i/(i+1) \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm S}/ N_0} \hspace{0.05cm}.$$
- From this it is very easy to calculate the symbol error probability:
- $$p_{\rm S} = {\rm Pr}({\cal{E}}) = 1 - {\rm Pr}({\cal{C}}) = \sum_{i = 1}^{M-1} (-1)^{i+1} \cdot {M-1 \choose i } \cdot \frac{1}{i+1} \cdot {\rm e }^{ - i/(i+1) \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm S}/ N_0} \hspace{0.05cm}.$$
- An upper bound $(p_{\rm S, \ max} ≥ p_{\rm S})$ is obtained due to the alternating signs if we consider only the first term $(i=1)$ of this sum:
- $$p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})} \hspace{0.05cm}.$$
In subtask (4), this bound is to be evaluated for a given ratio $E_{\rm B}/N_0$, where $E_{\rm B}$ is the average signal energy per bit:
- $$E_{\rm B} = \frac{ E_{\rm S} } { {\rm log_2}\hspace{0.1cm}(M)} \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Carrier Frequency Systems with Non-Coherent Demodulation".
- Reference is made in particular to the section "Non-coherent demodulation of multi-level FSK".
Questions
Solution
- In constellation $\rm B$ the orthogonality is not given. Rather $M = 3$ and $N = 2$ are valid here.
(2) For the binary FSK $(M = 2)$ applies with the abbreviation $x = E_{\rm S}/N_0 = 6$:
- $$p_{\rm S} = (-1)^{2} \cdot {1 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-x/2 } = {1}/{2} \cdot {\rm e }^{-3} \hspace{0.15cm}\underline{\approx 2.49 \%} \hspace{0.05cm}.$$
- Accordingly, for the ternary FSK $(M = 3)$ we obtain:
- $$p_{\rm S} = (-1)^{2} \cdot {2 \choose 1 } \cdot {1}/{2} \cdot {\rm e }^{-(1/2) \hspace{0.05cm} \cdot \hspace{0.05cm} x} + (-1)^{3} \cdot {2 \choose 2 } \cdot {1}/{3}\cdot {\rm e }^{-(2/3) \hspace{0.05cm} \cdot \hspace{0.05cm} x}= {\rm e }^{-3} - {1}/{3} \cdot {\rm e }^{-4} \approx 0.0498 - 0.0061 \hspace{0.15cm}\underline{ =4.37\%} \hspace{0.05cm}.$$
- Finally, for the quaternary FSK $(M = 4)$ we obtain:
- $$p_{\rm S} = (-1)^{2} \cdot {3 \choose 1 } \cdot \frac{{\rm e }^{-x/2}}{2} + (-1)^{3} \cdot {3 \choose 2 } \cdot \frac{{\rm e }^{-2x/3}}{3} + (-1)^{4} \cdot {4 \choose 3 } \cdot \frac{{\rm e }^{-3x/4 }}{4} = {3}/ {2} \cdot{\rm e }^{-3} - {\rm e }^{-4} + {\rm e }^{-4.5} \hspace{0.15cm}\underline{\approx 6.75\%} \hspace{0.05cm}.$$
(3) For equal $E_{\rm S}/N_0 = 6$, $p_{\rm S, \ max} ≥ p_{\rm S}$ always holds:
- $$M =2\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=2.49\%} = p_{\rm S} \hspace{0.05cm},$$
- $$M =3\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=4.98\%} > 4.37\% = p_{\rm S} \hspace{0.05cm},$$
- $$M =4\text{:} \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{0.15cm}\underline{=7.47\%} > {6.75\%} = p_{\rm S} \hspace{0.05cm}.$$
Analyzing the equation $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ in more detail, we see that this bound exactly specifies the "Union Bound":
- For the binary system, $1/2 \cdot {\rm e }^{-E_{\rm S}/(2N_{\rm 0})}$ gives the falsification probability, for example from $\boldsymbol{s}_1$ to $\boldsymbol{s}_2$ or vice versa.
- For the $M$–level system, the distance between $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$ is exactly the same. But also the points $\boldsymbol{s}_3, \ \text{... ,} \, \boldsymbol{s}_M$ are at the same distance from $\boldsymbol{s}_1$ or from $\boldsymbol{s}_2$.
- The "Union Bound" considers the distortion possibilities of a point to each of the generally $M–1$ other points by the factor $M -1$.
(4) With $E_{\rm B} = E_{\rm S}/{\rm log}_2(M)$ one obtains $p_{\rm S, \hspace{0.05cm}max} = (M-1)/2 \cdot {\rm e }^{-\log_2 \ (M) E_{\rm B}/(2N_{\rm 0})}$.
- The error probability becomes smaller as the level-number increases, because at constant $E_{\rm B}$ the energy $E_{\rm S}$ per symbol increases by the factor ${\rm log}_2 \, (M)$.
- The factor $M-1$ (considers the falsification possibilities of a signal space point) has less influence than the increase of the negative exponent:
- $$M =2\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{ 2} \cdot {\rm e }^{-3} \hspace{0.15cm} \underline{= 2.49\%} \hspace{0.05cm},$$
- $$M =3\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm e }^{-4.755} \hspace{0.5cm} \underline{= 0.86\%} \hspace{0.05cm},$$
- $$M =4\hspace{-0.1cm}: \hspace{0.2cm} p_{\rm S, \hspace{0.05cm}max} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {3}/{ 2} \cdot {\rm e }^{-6} \hspace{0.15cm} \underline{=0.37\%} \hspace{0.05cm}.$$