Difference between revisions of "Aufgaben:Exercise 4.5: On the Extrinsic L-values again"
m (Guenter moved page Aufgabe 4.5: Nochmals zu den extrinsischen L–Werten to Exercise 4.5: On the Extrinsic L-values again) |
|||
| Line 2: | Line 2: | ||
[[File:P_ID3026__KC_A_4_5_v2.png|right|frame|Tabelle nach dem ersten $L_{\rm E}(i)$–Ansatz]] | [[File:P_ID3026__KC_A_4_5_v2.png|right|frame|Tabelle nach dem ersten $L_{\rm E}(i)$–Ansatz]] | ||
| − | + | We assume as in [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_LLRs|"theory section"]] from <i>single parity–check code</i> $\rm SPC \, (3, \, 2, \, 2)$ . The possible code words are $\underline{x} \hspace{-0.01cm}\in \hspace{-0.01cm} | |
\{ \underline{x}_0,\hspace{0.05cm} | \{ \underline{x}_0,\hspace{0.05cm} | ||
\underline{x}_1,\hspace{0.05cm} | \underline{x}_1,\hspace{0.05cm} | ||
| Line 16: | Line 16: | ||
\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm}.$$ | \underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm}.$$ | ||
| − | In | + | In the exercise we mostly use the second (bipolar) representation of the code symbols: $x_i ∈ \{+1, -1\}$. |
| − | * | + | *It is not that the $\rm SPC \, (3, \, 2, \, 2)$ would be of much practical interest, since, for example, in <i>hard decision</i> because of $d_{\rm min} = 2$ only one error can be detected and none can be corrected. However, the code is well suited for practice and demonstration purposes because of the manageable effort involved. |
| − | * | + | *With ''iterative symbol-wise decoding'' one can also correct one error. In the present code, the extrinsic $L$–values $\underline{L}_{\rm E} = \big (L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3)\big )$ must be calculated according to the following equation. |
:$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \hspace{0.05cm}\right ]}.$$ | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \hspace{0.05cm}\right ]}.$$ | ||
| − | : | + | :Here $\underline{x}^{(-1)}$ denotes all symbols except $x_i$ and is thus a vector of length $n - 1 = 2$. |
| − | + | As the '''first $L_{\rm E}(i)$ approach''' we refer to the approach corresponding to the equations | |
:$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$ | :$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$ | ||
:$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$ | :$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$ | ||
:$$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$ | :$$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$ | ||
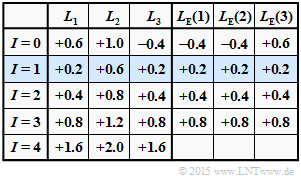
| − | '''(1)''' | + | '''(1)''' This $L_{\rm E}(i)$ approach underlies the results table above (red entries), assuming the following a posteriori $L$ values: |
:$$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm}{\rm kurz\hspace{-0.1cm}:}\hspace{0.25cm} | :$$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm}{\rm kurz\hspace{-0.1cm}:}\hspace{0.25cm} | ||
L_1 = +1.0\hspace{0.05cm},\hspace{0.05cm} | L_1 = +1.0\hspace{0.05cm},\hspace{0.05cm} | ||
| Line 36: | Line 36: | ||
L_3 = -1.0\hspace{0.05cm}.$$ | L_3 = -1.0\hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' The extrinsic $L$–values for the zeroth iteration result in (derivation in [[Aufgaben:Exercise_4.5Z:_Tangent_Hyperbolic_and_Inverse|"Exercise 4.5Z"]]): |
:$$L_{\rm E}(1) = -0.1829, \ L_{\rm E}(2) = -0.4337, \ L_{\rm E}(3) = +0.1829.$$ | :$$L_{\rm E}(1) = -0.1829, \ L_{\rm E}(2) = -0.4337, \ L_{\rm E}(3) = +0.1829.$$ | ||
| − | '''(3)''' | + | '''(3)''' The a posteriori values at the beginning of the first iteration are thus |
:$$\underline{L}^{(I=1)} = \underline{L}^{(I=0)} + \underline{L}_{\hspace{0.02cm}\rm E}^{(I=0)} = | :$$\underline{L}^{(I=1)} = \underline{L}^{(I=0)} + \underline{L}_{\hspace{0.02cm}\rm E}^{(I=0)} = | ||
(+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) | (+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) | ||
\hspace{0.05cm} . $$ | \hspace{0.05cm} . $$ | ||
| − | '''(4)''' | + | '''(4)''' From this, the new extrinsic values for the iteration loop $I = 1$ are as follows: |
:$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(-0.0337/2) \cdot {\rm tanh}(-0.8171/2) \big ] = 0.0130 = -L_{\rm E}(3)\hspace{0.05cm},$$ | :$$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(-0.0337/2) \cdot {\rm tanh}(-0.8171/2) \big ] = 0.0130 = -L_{\rm E}(3)\hspace{0.05cm},$$ | ||
:$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(+0.8171/2) \cdot {\rm tanh}(-0.8171/2) \big ] = - 0.3023\hspace{0.05cm}.$$ | :$$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(+0.8171/2) \cdot {\rm tanh}(-0.8171/2) \big ] = - 0.3023\hspace{0.05cm}.$$ | ||
| − | + | Further, one can see from the above table: | |
| − | * | + | * A hard decision according to the signs before the first iteration $(I = 0)$ fails, since $(+1, +1, -1)$ is not a valid $\rm SPC \, (3, \, 2, \, 2)$–code word. |
| − | * | + | * But already after $I = 1$ iterations, a hard decision yields a valid code word, namely $\underline{x}_2 = (+1, -1, -1)$. Also in later graphs, the rows with correct HD decisions for the first time are highlighted in blue. |
| − | * | + | * Hard decisions after further iterations $(I ≥ 2)$ each lead to the same code word $\underline{x}_2$. This statement is not only valid for this example, but in general. |
| − | + | Besides, in this exercise we consider a '''second $L_{\rm E}(i)$ approach''', which is given here for the example of the first symbol $(i = 1)$: | |
:$${\rm sign} \big[L_{\rm E}(1)\big] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} \big[L_{\rm E}(2)\big] \cdot {\rm sign} \big[L_{\rm E}(3)\big]\hspace{0.05cm},\hspace{0.8cm} | :$${\rm sign} \big[L_{\rm E}(1)\big] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} \big[L_{\rm E}(2)\big] \cdot {\rm sign} \big[L_{\rm E}(3)\big]\hspace{0.05cm},\hspace{0.8cm} | ||
|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$ | |L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$ | ||
| − | + | This second approach is based on the assumption that the reliability of $L_{\rm E}(i)$ is essentially determined by the most unreliable neighbor symbol. The better (larger) input–LLR is completely disregarded. – Let us consider two examples for this: | |
| − | |||
| − | |||
| − | |||
| + | '''(1)''' For $L_2 = 1.0$ and $L_3 = 5.0$ we get for example | ||
| + | * after the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(2.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.4559) = 0.984\hspace{0.05cm},$ | ||
| + | * according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}5.0 \big ) = 1.000 \hspace{0.05cm}.$ | ||
| − | |||
| − | |||
| − | |||
| + | '''(2)''' On the other hand one obtains for $L_2 = L_3 = 1.0$ | ||
| + | * according to the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(0.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.2135) = 0.433\hspace{0.05cm},$ | ||
| + | * according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}1.0 \big ) = 1.000 \hspace{0.05cm}.$ | ||
| − | |||
| + | One can see the clear discrepancy between the two approaches. The second approach (approximation) is clearly more positive than the first (correct) approach. However, it is actually only important that the iterations lead to the desired decoding result. | ||
| − | + | ||
| − | * | + | Hints: |
| − | * | + | *The exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder|"Soft–in Soft–out Decoder"]]. |
| − | * | + | *Referred to in particular [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_LLRs|"For calculation of extrinsic L values"]]. |
| − | * | + | * Only the '''second solution approach''' is treated here. |
| + | * For the first solution approach we refer to the [[Exercises:Exercise_4.5Z:_Tangent_Hyperbolic_and_Inverse|"Exercise 4.5Z"]] . | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
{Es gelte $\underline{L} = (+1.0, +0.4, -1.0)$. Ermitteln Sie die extrinsischen $L$–Werte nach dem '''zweiten $L_{\rm E}(i)$–Ansatz''' ohne vorherige Iteration $\underline{(I = 0)}$. | {Es gelte $\underline{L} = (+1.0, +0.4, -1.0)$. Ermitteln Sie die extrinsischen $L$–Werte nach dem '''zweiten $L_{\rm E}(i)$–Ansatz''' ohne vorherige Iteration $\underline{(I = 0)}$. | ||
Revision as of 01:03, 30 October 2022
We assume as in "theory section" from single parity–check code $\rm SPC \, (3, \, 2, \, 2)$ . The possible code words are $\underline{x} \hspace{-0.01cm}\in \hspace{-0.01cm} \{ \underline{x}_0,\hspace{0.05cm} \underline{x}_1,\hspace{0.05cm} \underline{x}_2,\hspace{0.05cm} \underline{x}_3\}$ mit
- $$\underline{x}_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm bzw. } \hspace{0.35cm} \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm},$$
- $$\underline{x}_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm bzw. } \hspace{0.35cm} \underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$
- $$\underline{x}_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}0\hspace{-0.03cm},\hspace{0.05cm}1)\hspace{0.35cm}{\rm bzw. } \hspace{0.35cm} \underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}-1)\hspace{0.05cm},$$
- $$\underline{x}_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1\hspace{-0.03cm},\hspace{0.05cm}1\hspace{-0.03cm},\hspace{0.05cm}0)\hspace{0.35cm}{\rm bzw. } \hspace{0.35cm} \underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm}-1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{0.05cm}.$$
In the exercise we mostly use the second (bipolar) representation of the code symbols: $x_i ∈ \{+1, -1\}$.
- It is not that the $\rm SPC \, (3, \, 2, \, 2)$ would be of much practical interest, since, for example, in hard decision because of $d_{\rm min} = 2$ only one error can be detected and none can be corrected. However, the code is well suited for practice and demonstration purposes because of the manageable effort involved.
- With iterative symbol-wise decoding one can also correct one error. In the present code, the extrinsic $L$–values $\underline{L}_{\rm E} = \big (L_{\rm E}(1), \ L_{\rm E}(2), \ L_{\rm E}(3)\big )$ must be calculated according to the following equation.
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \hspace{0.05cm}\right ]}.$$
- Here $\underline{x}^{(-1)}$ denotes all symbols except $x_i$ and is thus a vector of length $n - 1 = 2$.
As the first $L_{\rm E}(i)$ approach we refer to the approach corresponding to the equations
- $$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$
- $$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_3/2) \right ] \hspace{0.05cm},$$
- $$L_{\rm E}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \left [{\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \right ] \hspace{0.05cm}.$$
(1) This $L_{\rm E}(i)$ approach underlies the results table above (red entries), assuming the following a posteriori $L$ values:
- $$\underline {L}_{\rm APP} = (+1.0\hspace{0.05cm},\hspace{0.05cm}+0.4\hspace{0.05cm},\hspace{0.05cm}-1.0) \hspace{0.5cm}{\rm kurz\hspace{-0.1cm}:}\hspace{0.25cm} L_1 = +1.0\hspace{0.05cm},\hspace{0.05cm} L_2 = +0.4\hspace{0.05cm},\hspace{0.05cm} L_3 = -1.0\hspace{0.05cm}.$$
(2) The extrinsic $L$–values for the zeroth iteration result in (derivation in "Exercise 4.5Z"):
- $$L_{\rm E}(1) = -0.1829, \ L_{\rm E}(2) = -0.4337, \ L_{\rm E}(3) = +0.1829.$$
(3) The a posteriori values at the beginning of the first iteration are thus
- $$\underline{L}^{(I=1)} = \underline{L}^{(I=0)} + \underline{L}_{\hspace{0.02cm}\rm E}^{(I=0)} = (+0.8171\hspace{0.05cm},\hspace{0.05cm}-0.0337\hspace{0.05cm},\hspace{0.05cm}-0.8171) \hspace{0.05cm} . $$
(4) From this, the new extrinsic values for the iteration loop $I = 1$ are as follows:
- $$L_{\rm E}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(-0.0337/2) \cdot {\rm tanh}(-0.8171/2) \big ] = 0.0130 = -L_{\rm E}(3)\hspace{0.05cm},$$
- $$L_{\rm E}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(+0.8171/2) \cdot {\rm tanh}(-0.8171/2) \big ] = - 0.3023\hspace{0.05cm}.$$
Further, one can see from the above table:
- A hard decision according to the signs before the first iteration $(I = 0)$ fails, since $(+1, +1, -1)$ is not a valid $\rm SPC \, (3, \, 2, \, 2)$–code word.
- But already after $I = 1$ iterations, a hard decision yields a valid code word, namely $\underline{x}_2 = (+1, -1, -1)$. Also in later graphs, the rows with correct HD decisions for the first time are highlighted in blue.
- Hard decisions after further iterations $(I ≥ 2)$ each lead to the same code word $\underline{x}_2$. This statement is not only valid for this example, but in general.
Besides, in this exercise we consider a second $L_{\rm E}(i)$ approach, which is given here for the example of the first symbol $(i = 1)$:
- $${\rm sign} \big[L_{\rm E}(1)\big] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} \big[L_{\rm E}(2)\big] \cdot {\rm sign} \big[L_{\rm E}(3)\big]\hspace{0.05cm},\hspace{0.8cm} |L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) \hspace{0.05cm}.$$
This second approach is based on the assumption that the reliability of $L_{\rm E}(i)$ is essentially determined by the most unreliable neighbor symbol. The better (larger) input–LLR is completely disregarded. – Let us consider two examples for this:
(1) For $L_2 = 1.0$ and $L_3 = 5.0$ we get for example
- after the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(2.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.4559) = 0.984\hspace{0.05cm},$
- according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}5.0 \big ) = 1.000 \hspace{0.05cm}.$
(2) On the other hand one obtains for $L_2 = L_3 = 1.0$
- according to the first approach: $L_{\rm E}(1) =2 \cdot {\rm tanh}^{-1} \big [{\rm tanh}(0.5) \cdot {\rm tanh}(0.5) \big ] =2 \cdot {\rm tanh}^{-1}(0.2135) = 0.433\hspace{0.05cm},$
- according to the second approach: $|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \big ( 1.0\hspace{0.05cm}, \hspace{0.05cm}1.0 \big ) = 1.000 \hspace{0.05cm}.$
One can see the clear discrepancy between the two approaches. The second approach (approximation) is clearly more positive than the first (correct) approach. However, it is actually only important that the iterations lead to the desired decoding result.
Hints:
- The exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Referred to in particular "For calculation of extrinsic L values".
- Only the second solution approach is treated here.
- For the first solution approach we refer to the "Exercise 4.5Z" .
Questions
Musterlösung
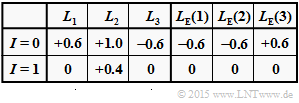
(1) Entsprechend dem zweiten $L_{\rm E}(i)$–Ansatz gilt:
- $${\rm sign} [L_{\rm E}(1)] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm sign} [L_{\rm E}(2)] \cdot {\rm sign} [L_{\rm E}(3)] = -1 \hspace{0.05cm},$$
- $$|L_{\rm E}(1)| \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Min} \left ( |L_{\rm E}(2)|\hspace{0.05cm}, \hspace{0.05cm}|L_{\rm E}(3)| \right ) = {\rm Min} \left ( 0.4\hspace{0.05cm}, \hspace{0.05cm}1.0 \right ) = 0.4\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(1) \hspace{0.15cm} \underline{-0.4}\hspace{0.05cm}.$$
- In gleicher Weise erhält man:
- $$L_{\rm E}(2) \hspace{0.15cm} \underline{-1.0}\hspace{0.05cm}, \hspace{0.3cm} L_{\rm E}(3) \hspace{0.15cm} \underline{+0.4}\hspace{0.05cm}.$$
(2) Die Aposteriori–$L$–Werte zu Beginn der ersten Iteration $(I = 1)$ ergeben sich aus der Summe der bisherigen $L$–Werte (für $I = 0$) und den unter (1) berechneten extrinsischen Werten:
- $$L_1 = L_{\rm APP}(1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1.0 + (-0.4)\hspace{0.15cm} \underline{=+0.6}\hspace{0.05cm},$$
- $$L_2 = L_{\rm APP}(2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.4 + (-1.0)\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm},$$
- $$L_3 = L_{\rm APP}(3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (-1.0) + 0.4\hspace{0.15cm} \underline{=-0.6}\hspace{0.05cm}.$$
(3) Wie aus obiger Tabelle hervorgeht, sind die Lösungsvorschläge 1 und 2 richtig im Gegensatz zur Antwort 3:
- Mit jeder neuen Iteration werden die Beträge von $L(1), \ L(2)$ und $L(3)$ signifikant größer.
(4) Wie aus nebenstehender Tabelle hervorgeht, sind die Antworten 1 und 3 richtig:
- Die Entscheidung fällt also für das Codewort $\underline{x}_0 = (+1, +1, +1)$.
- Ab $I = 1$ wäre dies auch die Entscheidung von Hard Decision.
(5) Richtig sind die Antworten 2 und 3:
- Wegen $|L(3)| > |L(1)|$ gilt bereits ab $I = 1$: $L_1 < 0 \hspace{0.05cm},\hspace{0.2cm} L_2 > 0 \hspace{0.05cm},\hspace{0.2cm} L_3 < 0 \hspace{0.05cm}.$
- Ab dieser Iterationsschleife liefert Hard Decision das Codewort $\underline{x}_2 = (-1, +1, -1)$.
(6) Richtig sind der Lösungsvorschlag 3:
- Die nebenstehende Tabelle zeigt, dass unter der Voraussetzung $|L(1)| = |L(3)|$ ab der Iterationsschleife $I = 1$ alle extrinsischen $L$–Werte Null sind.
- Damit bleiben die Aposteriori–$L$–Werte auch für $I > 1$ konstant gleich $\underline{L} = (0., +0.4, 0.)$, was keinem Codewort zugeordnet werden kann.