Difference between revisions of "Aufgaben:Exercise 3.7Z: Which Code is Catastrophic?"
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Code_Description_with_State_and_Trellis_Diagram}} | {{quiz-Header|Buchseite=Channel_Coding/Code_Description_with_State_and_Trellis_Diagram}} | ||
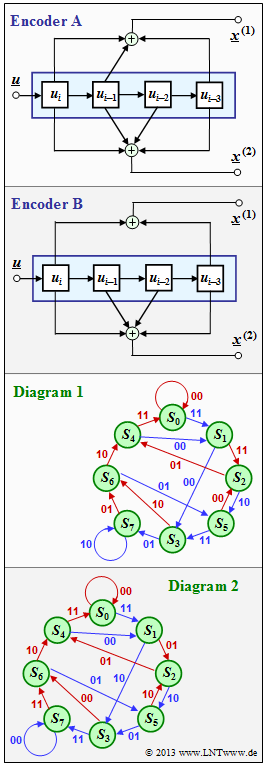
| − | [[File: | + | [[File:EN_KC_Z_3_7_neu.png|right|frame|Encoder for $m = 3$ and state transition diagram.]] |
The adjacent graph shows. | The adjacent graph shows. | ||
* two different $\text{ Coder A }$ and $\text{ Coder B}$, each with memory $m = 3$ (top), | * two different $\text{ Coder A }$ and $\text{ Coder B}$, each with memory $m = 3$ (top), | ||
Revision as of 18:13, 8 November 2022
The adjacent graph shows.
- two different $\text{ Coder A }$ and $\text{ Coder B}$, each with memory $m = 3$ (top),
- two state transition diagrams, labeled $\text{ diagram 1 }$ and $\text{ diagram 2 }$ (bottom).
In the last subtask, you are to decide which diagram belongs to $\text{ encoder A }$ and which to $\text{ encoder B}$.
First, the three transfer functions
- $G(D) = 1 + D + D^2 + D^3$,
- $G(D) = 1 + D^3$, and
- $G(D) = 1 + D + D^3$
are analyzed and then the initial sequences $\underline{x}$ under the condition
- $$\underline{u}= \underline{1}= (1, 1, 1, \text{...} \hspace{0.05cm}) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} U(D)= \frac{1}{1+D}$$
is calculated. These transfer functions are directly related to the outlined coders.
- Furthermore, it remains to be clarified which of the two codes is "catastrophic".
- One speaks of such when a finite number of transmission errors leads to an infinite number of decoding errors.
Hints:
- This exercise belongs to the chapter "Code description with state and trellis diagram".
- Reference is made in particular to the sections.
- Two more polynomial products in ${\rm GF}(2)$ are given:
- $$(1+D) \cdot (1+D^2) = 1+D +D^2+D^3\hspace{0.05cm},$$
- $$(1+D) \cdot (1+D+D^2) = 1+D^3\hspace{0.05cm}.$$
Questions
Solution
- The $D$ transform of the code sequence $\underline{x}$ is given by $U(D) = 1/(1+ D)$ to be.
- $$X(D)= \frac{1+D +D^2+D^3}{1+D}= 1 +D^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x}= (1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} ... \hspace{0.1cm})\hspace{0.05cm}.$$
- Consider $(1 + D) \cdot (1 + D^2) = 1 + D + D^2 + D^3$.
(2) Because of $(1 + D) \cdot (1 + D + D^2) = 1 + D^3$, solutions 3 and 4 are applicable here:
- $$X(D)= \frac{1+D^3}{1+D}= 1 +D + D^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{x}= (1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{0.05cm}.$$
(3) Only the proposed solution 1 is correct:
- The polynomial division $(1 + D + D^3)$ by $(1 + D)$ is not possible in the binary Galois field without a remainder.
- You get $X(D) = 1 + D^3 + D^4 + D^5 + \ \text{...} \hspace{0.05cm} $ ⇒ Output sequence $\underline{x} = (1, \, 0, \, 0, \, 1, \, 1, \, 1, \, \text{...} \hspace{0.05cm})$ which extends to infinity.
(4) Only the proposed solution 1 is correct:
- The transfer function matrix of $\text{ coder A }$ is:
- $${\boldsymbol{\rm G}}_{\rm A}(D)= \left (1 +D + D^3\hspace{0.05cm}, \hspace{0.15cm} 1+D +D^2+D^3 \right ) \hspace{0.05cm}.$$
- The first code bit in each case is therefore given by the sequence corresponding to subtask (3) and the second bit by the sequence corresponding to subtask (1):
- $$\underline{x}^{(1)}\hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} 1,\hspace{0.05cm} ... \hspace{0.1cm})\hspace{0.05cm}, \hspace{1cm} \underline{x}^{(2)}\hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{0.01cm})\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x}= (11,\hspace{0.05cm} 00,\hspace{0.05cm} 01,\hspace{0.05cm} 10,\hspace{0.05cm} 10,\hspace{0.05cm} 10,\hspace{0.05cm} \text{...} \hspace{0.05cm} \hspace{0.01cm})\hspace{0.05cm}.$$
(5) Applicable are suggested solutions 2 and 4:
- The transfer function of $\text{ coder B }$ is $\mathbf{G}_{\rm B} = (1 + D^3, \ 1 + D + D^2 + D^3)$.
- The first code sequence now results according to subtask (2), while $\underline{x}^{(2)}$ still corresponds to subtask (1).
- Thus we get here $\underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, \text{...} \hspace{0.05cm})$ ⇒ Solution suggestion 2.
- But solution proposition 4 is also correct. Under the assumption made here $\underline{u} = \underline{1}$ the code sequence $\underline{x}$ contains only five ones.
- In the next subtask this fact is taken up again.
(6) Correct are the proposed solutions 2 and 3:
WAs can be seen from state diagram 1, here the information sequence $\underline{u} = \underline{1} = (1, \, 1, \, 1, \, 1, \, 1, \, 1, \, \text{...} \hspace{0.05cm})$ to the code sequence $\underline{x} = (11, \, 00, \, 01, \, 10, \, 10, \, 10, \, ...)$. This means:
- To the $\text{ encoder A }$ belongs the state transition diagram 1.
- To $\text{ encoder B }$ belongs the state transition diagram 2 ⇒ Proposed solution 2.
For the $\text{ encoder B }$, the following statements hold:
- $\underline{u} = \underline{0} = (0, \, 0, \, 0, \, 0, \, 0, \, 0, \, \text{...} \hspace{0.05cm}) \hspace{0.35cm} \Rightarrow \hspace{0.35cm} \underline{x} = (00, \, 00, \, 00, \, 00, \, 00, \, 00, \, \text{...} \hspace{0.05cm})$,
- $\underline{u} = \underline{1} = (1, \, 1, \, 1, \, 1, \, 1, \, 1, \, \text{...} \hspace{0.05cm}) \hspace{0.35cm} \Rightarrow \hspace{0.35cm} \underline{x} = (11, \, 10, \, 11, \, 00, \, 00, \, 00, \, \text{...} \hspace{0.05cm})$.
Das bedeutet:
- With only five bit errors at positions 1, 2, 3, 5, 6, the zero sequence is decoded as a one sequence and vice versa.
- Such a code is called catastrophic ⇒ Solution suggestion 3.