Difference between revisions of "Aufgaben:Exercise 4.08: Repetition to the Convolutional Codes"
| Line 3: | Line 3: | ||
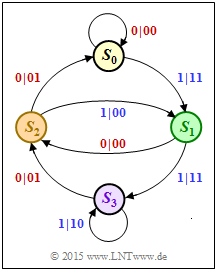
[[File:P_ID3033__KC_A_4_8_v2.png|right|frame|State transition diagram of a non-recursive code]] | [[File:P_ID3033__KC_A_4_8_v2.png|right|frame|State transition diagram of a non-recursive code]] | ||
| − | The turbo codes are based on convolutional codes, which are discussed in detail in the chapter [[Channel_Coding/Basics_of_Convolutional_Coding| "Basics of | + | The turbo codes are based on convolutional codes, which are discussed in detail in the chapter [[Channel_Coding/Basics_of_Convolutional_Coding| "Basics of Convolutional Coding"]] . |
| − | + | Starting from the adjacent state transition diagram, essential properties and characteristics of the considered rate $1/2$ convolutional code shall be determined, and we explicitly refer to the following theory pages: | |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Algebraic_and_Polynomial_Description#Systematic_convolutional_codes|"Systematic convolutional codes"]] |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Representation_in_the_state_transition_diagram|"Representation in the state transition diagram"]] |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Code_Description_with_State_and_Trellis_Diagram#Definition_of_the_free_distance|"Definition of the free distance"]] |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Algebraic_and_Polynomial_Description#GF.282.29_description_forms_of_a_digital_filter|"GF(2) description forms of a digital filter"]] |
| − | #[[Channel_Coding/ | + | #[[Channel_Coding/Algebraic_and_Polynomial_Description#Application_of_the_D.E2.80.93transform_to_rate_.7F.27.22.60UNIQ-MathJax160-QINU.60.22.27.7F_convolution_encoders| "Application of $D$–transformation to rate 1/n convolutional codes."]] |
| − | + | In the state transition diagram, the state $S_0$ is always assumed. Two arrows go from each state. The label is "$u_i \hspace{0.05cm}|\hspace{0.05cm} x_i^{(1)}x_i^{(2)}$". For a systematic code, this holds: | |
* Das erste Codebit ist identisch mit dem Informationsbit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}$ | * Das erste Codebit ist identisch mit dem Informationsbit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}$ | ||
* Das zweite Codebit ist das Prüfbit (Paritybit): $\ x_i^{(2)} = p_i ∈ \{0, \, 1\}$. | * Das zweite Codebit ist das Prüfbit (Paritybit): $\ x_i^{(2)} = p_i ∈ \{0, \, 1\}$. | ||
Revision as of 16:18, 25 November 2022
The turbo codes are based on convolutional codes, which are discussed in detail in the chapter "Basics of Convolutional Coding" .
Starting from the adjacent state transition diagram, essential properties and characteristics of the considered rate $1/2$ convolutional code shall be determined, and we explicitly refer to the following theory pages:
- "Systematic convolutional codes"
- "Representation in the state transition diagram"
- "Definition of the free distance"
- "GF(2) description forms of a digital filter"
- "Application of $D$–transformation to rate 1/n convolutional codes."
In the state transition diagram, the state $S_0$ is always assumed. Two arrows go from each state. The label is "$u_i \hspace{0.05cm}|\hspace{0.05cm} x_i^{(1)}x_i^{(2)}$". For a systematic code, this holds:
- Das erste Codebit ist identisch mit dem Informationsbit: $\ x_i^{(1)} = u_i ∈ \{0, \, 1\}$
- Das zweite Codebit ist das Prüfbit (Paritybit): $\ x_i^{(2)} = p_i ∈ \{0, \, 1\}$.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Grundlegendes zu den Turbocodes.
- In den Fragen zu dieser Aufgabe werden folgende semi–infinite Vektoren verwendet:
- Informationssequenz $\ \underline{u} = (u_1, \, u_2, \text{ ...})$,
- Paritysequenz $\ \underline{p} = (p_1, \, p_2, \text{ ...})$,
- Impulsantwort $\ \underline{g} = (g_1, \, g_2, \text{ ...})$; diese ist gleich der Paritysequenz $\underline{p}$ für $\underline{u} = (1, \, 0, \, 0, \text{ ...})$.
Fragebogen
Musterlösung
- Die Impulsantwort $\underline{g}$ ist gleich der Ausgangsfolge $\underline{p}$ für die Eingangsfolge $\underline{u} = (1, \, 0, \, 0, \, 0, \text{ ...})$.
- Ausgehend vom Zustand $S_0$ ergeben sich im Zustandsübergangsdiagramm folgende Übergänge:
- $$S_0 → S_1 → S_2 → S_0 → S_0 → S_0 → \text{ ...} \hspace{0.6cm} \Rightarrow \hspace{0.5cm} {\rm Impulsantwort} \text{:} \hspace{0.2cm} \underline{g} = (1, \, 0, \, 1, \, 0, \, 0) \, .$$
- Für ein nichtrekursives Filter mit Gedächtnis $m$ gilt $g_i ≡ 0$ für $i > m$. In unserem Beispiel ist $m = 2$.
- Der Lösungsvorschlag 1 gilt dagegen für das rekursive Filter (RSC) entsprechend der Aufgabe 4.9.
(2) Es sei $\underline{u} = (1, \, 0, \, 0, \, 1, \, 0, \, 0, \, u_7)$ und $\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, ...)$. Dann gilt für die Paritysequenz aufgrund der Linearität:
- $$\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm} 0,\hspace{0.05cm} u_7\hspace{0.05cm} ) * (\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0 ,\hspace{0.05cm} 0,\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...})= $$
- $$\ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm}0, \hspace{0.05cm} \text{ ...} \hspace{0.05cm})\hspace{0.05cm}\oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm}0, \hspace{0.05cm} \text{ ...}\hspace{0.05cm})\hspace{0.05cm}\oplus (\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} u_7,\hspace{0.05cm} 0,\hspace{0.05cm}u_7, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) $$
- $$\Rightarrow \hspace{0.3cm}\underline{p} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}0,\hspace{0.05cm}1,\hspace{0.05cm}\hspace{0.05cm}1,\hspace{0.05cm} 0,\hspace{0.05cm} 1,\hspace{0.05cm} u_7,\hspace{0.05cm} 0,\hspace{0.05cm}u_7, \hspace{0.05cm} \text{ ...} \hspace{0.05cm}) \hspace{0.05cm}.$$
Richtig sind also die Lösungsvorschläge 1 und 2 im Gegensatz zur Antwort 3:
- Für $u_7 = 1$ gilt $p_7 = 1, \ p_8 = 0, \ p_9 = 1$ und $p_i ≡ 0$ für $i > 9$.
(3) Richtig ist der Lösungsvorschlag 2:
- Aus dem Zustandsübergangsdiagramm erkennt man die Codeparameter $k = 1$ und $n = 2$.
- Das heißt: Die Übertragungsfunktionsmatrix $\mathbf{G}(D)$ besteht aus zwei Elementen ⇒ der Vorschlag 3 ist falsch.
- Die erste Komponente von $\mathbf{G}(D)$ ist tatsächlich 1, da ein systematischer Code vorliegt: $\ \underline{x}^{(1)} ≡ \underline{z}$.
- Die zweite Komponente von $\mathbf{G}(D)$ ist gleich der $D$–Transformierten der Impulsantwort $\underline{g}$, wobei die Dummy–Variable $D$ eine Verzögerung um ein Bit angibt:
- $$\underline{g}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{ ...}\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G^{(2)}(D) = 1+ D^2\hspace{0.05cm}. $$
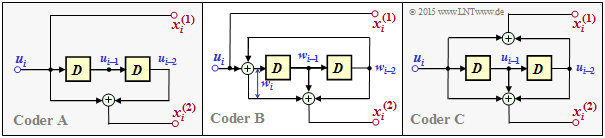
Über die Fragestellung hinausgehend betrachten wir hier auch noch die vorliegende Filterstruktur:
In der Grafik ist der hier betrachtete Coder als Coder $\rm A$ links dargestellt.
- Dieser ist ebenso wie der Coder $\rm B$ systematisch, und
- basiert im Gegensatz zu Coder $\rm B$ aber auf einem nichtrekursiven Filter.
- Der Coder $\rm C$ hat ebenfalls eine nichtrekursive Struktur, ist aber nicht systematisch.
- Die äquivalente systematische Repräsentation von Coder $\rm C$ ist der Coder $\rm B$.
(4) Richtig sind die Lösungsvorschläge 2 und 3:
- Die Aufgabe könnte in gleicher Weise gelöst werden wie die Teilaufgabe (2).
- Wir wählen hier aber zur Abwechslung den Weg über die $D$–Transformation:
- $$\underline{u}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D^2 + D^5$$
- $$\Rightarrow \hspace{0.3cm} P(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} U(D) \cdot G(D) = (1+ D^2 + D^5) \cdot (1+ D^2 ) =1+ D^2 + D^5 + D^2 + D^4 + D^7 = 1+ D^4 + D^5 + D^7$$
- $$\Rightarrow \hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm})\hspace{0.05cm}.$$
(5) Die freie Distanz $d_{\rm F}$ eines Faltungscoders ist gleich der Anzahl der Bits, durch die sich zwei beliebigen Sequenzen dieses Codes mindestens unterscheiden.
- Gehen wir wie allgemein üblich als Bezugsgröße von der Nullsequenz $\underline{0} \ \Rightarrow \ S_0 → S_0 → S_0 → S_0 → \ \text{ ...} \ $ aus, so ergibt sich $d_{\rm F}$ gleichzeitig als das minimale Hamming–Gewicht (Anzahl der Einsen) einer zulässigen Codesequenz $\underline{x} ≠ \underline{0}$.
- Aus dem Zustandsübergangsdiagramm erkennt man, dass die freie Distanz zum Beispiel durch den Pfad
- $$ S_0 → S_0 → S_1 → S_2 → S_0 → S_0 → \text{ ...}$$
- gekennzeichnet ist, also durch die Codesequenz $00 \hspace{0.1cm} 11 \hspace{0.1cm} 00 \hspace{0.1cm} 01 \hspace{0.1cm} 00 \text{ ...} \ .$
- Dementsprechend gilt für die freie Distanz dieses nichtrekursiven Codes: $\hspace{0.2cm} d_{\rm F} \ \underline{= 3}$.