Aufgaben:Exercise 4.5: Pseudo Noise Modulation

• Return to book

Models of PN modulation (top) and BPSK (bottom)

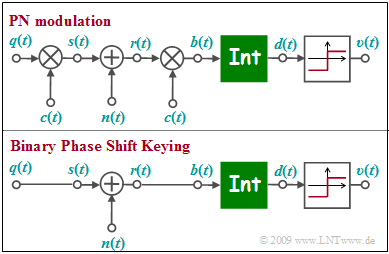
The upper diagram shows the equivalent circuit of  $\rm PN$  modulation  $($Direct-Sequence Spread Spectrum, abbreviated  $\rm DS–SS)$  in the equivalent low-pass range,  based on AWGN noise  $n(t)$. 

Shown below is the low-pass model of binary phase shift keying  $\rm (BPSK)$. 

• The low-pass transmitted signal  $s(t)$  is set equal to the rectangular source signal  $q(t) ∈ \{+1, –1\}$  with rectangular duration  $T$  for reasons of uniformity.

• The function of the integrator can be described as follows:

$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$

• The two models differ by multiplication with the  $±1$  spreading signal  $c(t)$  at transmitter and receiver,  where only the spreading factor  $J$  is known from  $c(t)$. 

It has to be investigated whether the lower BPSK model can also be used for PN modulation and whether the BPSK error probability

$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$

is also valid for PN modulation,  or how the given equation should be modified.

Notes:

• This exercise mostly refers to the page  "Telecommunications Aspects of UMTS".

• For the solution of this exercise,  the specification of the specific spreading sequence  $($M-sequence or Walsh function$)$  is not important.

Questions

1

Which detection signal values are possible with BPSK  (in the noise-free case)?

	$d(νT)$  can be Gaussian distributed.
	$d(νT)$  can take the values  $+1$,  $0$  and  $-1$.
	Only the values  $d(νT) = +1$  and  $d(νT) = -1$  are possible.

2

Which values are possible in PN modulation  (in the noise-free)  case?

	$d(νT)$  can be Gaussian distributed.
	$d(νT)$  can take the values  $+1$,  $0$  and  $-1$.
	Only the values  $d(νT) = +1$  and  $d(νT) = -1$  are possible.

3

What modification must be made to the BPSK model to make it applicable to PN modulation?

	The noise  $n(t)$  must be replaced by  $n'(t) = n(t) · c(t)$.
	The integration must now be done over  $J · T$.
	The noise power  $σ_n^2$  must be reduced by a factor of  $J$.

4

What is the bit error probability  $(p_{\rm B})$  for  $10 \lg \ (E_{\rm B}/N_0) = 6\ \rm dB$  for PN modulation?   Note:   For BPSK applies in this case:   $p_{\rm B} ≈ 2.3 · 10^{–3}$.

	The larger  $J$  is chosen, the smaller  $p_{\rm B}$ is.
	The larger  $J$  is chosen, the larger  $p_{\rm B}$ is.
	Independent of  $J$,  the value  $p_{\rm B} ≈ 2.3 · 10^{–3}$ is always obtained.

Solution

Solution

(1)  The  last solution  is correct:

• We are dealing here with an optimal receiver.
• Without noise,  the signal  $b(t)$  within each bit is constantly equal to  $+1$  or  $-1$.
• From the given equation for the integrator

$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t $$

it follows that  $d(νT)$  can take only the values  $+1$  and  $-1$. 

(2)  Again the  last solution  is correct:

• In the noise– and interference-free case   ⇒   $n(t) = 0$,  the twofold multiplication by  $c(t) ∈ \{+1, –1\}$  can be omitted,
• so that the upper model is identical to the lower model.

(3)  Solution 1  is correct:

• Since both models are identical in the noise-free case,  only the noise signal has to be adjusted:   $n'(t) = n(t) · c(t)$.
• In contrast,  the other two solutions are not applicable:
• The integration must still be done over  $T = J · T_c$  and the PN modulation does not reduce the AWGN noise.

(4)  The  last solution  is correct:

• Multiplying the AWGN noise by the high-frequency  $±1$ signal  $c(t)$,  the product is also Gaussian and white.
• Because of  ${\rm E}\big[c^2(t)\big] = 1$,  the noise variance is not changed either.  Thus:
• The equation  $p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt {{2 E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$  valid for BPSK is also applicable for PN modulation,  independent of spreading factor  $J$  and specific spreading sequence.
• Ergo:  For AWGN noise,  band spreading neither increases nor decreases the error probability.