Exercise 4.5: Locality Curve for DSB-AM

• Return to book

Wir betrachten ein ähnliches Übertragungsszenario wie in der Aufgabe 4.4:

• ein sinusförmiges Nachrichtensignal mit Amplitude $A_{\rm N} = 2 \ \text{V}$ und Frequenz $f_{\rm N} = 10 \ \text{kHz}$,
• ZSB-Amplitudenmodulation ohne Trägerunterdrückung mit Trägerfrequenz $f_{\rm T} = 50 \ \text{kHz}$.

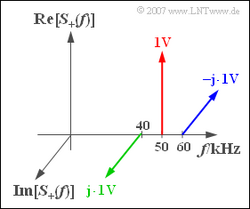
Nebenstehend sehen Sie die Spektralfunktion $S_+(f)$ des analytischen Signals $s_+(t)$ . Berücksichtigen Sie bei der Lösung, dass das äquivalente Tiefpass-Signal auch in der Form

$$s_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \phi(t)} $$

dargestellt werden kann, wobei $a(t) ≥ 0$ gelten soll. Für $\phi(t)$ ist der Wertebereich $–\pi < \phi(t) \leq +\pi$ zulässig und es gilt die allgemeingültige Gleichung:

$$\phi(t)= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\left[s_{\rm TP}(t)\right]}{{\rm Re}\left[s_{\rm TP}(t)\right]}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Sie können Ihre Lösung mit dem Interaktionsmodul Ortskurve – Darstellung des äquivalenten Tiefpass-Signals überprüfen.

Fragebogen

1

Berechnen Sie das äquivalente Tiefpass-Signal $s_{\rm TP}(t)$ im Frequenz– und Zeitbereich. Welchen Wert besitzt $s_{\rm TP}(t)$ zum Startzeitpunkt $t$ = 0?

$\text{Re}[s_{\text{TP}}(t=0 \mu \text{s})]$  =  $\text{V}$

$\text{Im}[s_{\text{TP}}(t=0 \mu \text{s})]$  =  $\text{V}$

2

Welche Werte weist $s_{\rm TP}(t)$ zu den Zeitpunkten $t = $T_0/10$, $T_0/4$, $3T_0/4$ und $T_0$ = 100 μs auf? Zeigen Sie, dass alle Werte rein reell sind.

$\text{Re}[s_{\text{TP}}(t=10 \mu \text{s})]$  =  $\text{V}$

$\text{Re}[s_{\text{TP}}(t=25 \mu \text{s})] $  =  $\text{V}$

$\text{Re}[s_{\text{TP}}(t=75 \mu \text{s})]$  =  $\text{V}$

$\text{Re}[s_{\text{TP}}(t=100 \mu \text{s})]$  =  $\text{V}$

3

Wie lautet die Betragsfunktion $a(t)$? Welche Werte ergeben sich zu den Zeiten $t = 25 \ \mu \text{s}$ und $t = 75 \ \mu \text{s}$?

$a(t=25 \ \mu \text{s})$  =  $\text{V}$

$a(t=75 \ \mu \text{s})$  =  $\text{V}$

4

Geben Sie die Phasenfunktion $\phi(t)$ allgemein an. Welche Werte ergeben sich zu den Zeiten $t = 25 \ \mu \text{s}$ und $t = 75 \ \mu \text{s}$?

$\phi(t=25 \ \mu \text{s}) =$ Grad

$\phi(t=75\ \mu \text{s}) =$ Grad

Musterlösung

Solution

1. Verschiebt man alle Diraclinien jeweils um $f_T$ = 50 kHz nach links, so liegen diese bei –10 kHz, 0 und +10 kHz. Die Gleichung $s_{TP}(t)$ lautet mit $\omega_10$ = 2 $π\pi \cdot$ 10 kHz:

$$s_{\rm TP}(t) = {\rm 1 \hspace{0.05cm} V} - {\rm j}\cdot {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }+{\rm j}\cdot {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }$$

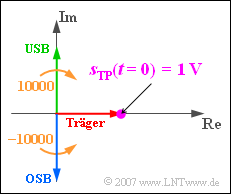
$$\Rightarrow \hspace{0.3cm} s_{\rm TP}(t = 0) = {\rm 1 \hspace{0.05cm} V} - {\rm j}\cdot {\rm 1 \hspace{0.05cm} V} +{\rm j}\cdot {\rm 1 \hspace{0.05cm} V}= {\rm 1 \hspace{0.05cm} V}.$$

$$\Rightarrow \hspace{0.3cm} {\rm Re}[s_{\rm TP}(t = 0) ] \hspace{0.15 cm}\underline{= {\rm 1 \hspace{0.05cm} V}}, \hspace{0.2cm}{\rm Im}[s_{\rm TP}(t = 0) ] \hspace{0.15 cm}\underline{= 0} .$$

2. Obige Gleichung kann man nach dem Satz von Euler mit $T_0 = 1/f_N = 100$ Mikrosekunden wie folgt umformen:

$$\frac{s_{\rm TP}(t)}{{\rm 1 \hspace{0.05cm} V}}\hspace{-0.05cm} =\hspace{-0.05cm}1\hspace{-0.05cm} - \hspace{-0.05cm}{\rm j}\cdot \cos({ \omega_{\rm 10}\hspace{0.05cm} t }) \hspace{-0.05cm}+\hspace{-0.05cm} \sin({ \omega_{\rm 10}\hspace{0.05cm} t }) \hspace{-0.05cm}+\hspace{-0.05cm}{\rm j}\cdot \cos({ \omega_{\rm 10}\hspace{0.05cm} t })\hspace{-0.05cm} + \hspace{-0.05cm} \sin({ \omega_{\rm 10}\hspace{0.05cm} t }) = 1+2 \cdot \sin(2 \pi \frac{t}{T_0}) .$$

Damit ist gezeigt, dass $s_{TP}(t)$ für alle Zeiten $t$ reell ist. Für die gesuchten Zahlenwerte erhält man:

$$s_{\rm TP}(t = {\rm 10 \hspace{0.05cm} \mu s}) = {\rm 1 \hspace{0.05cm} V} \cdot \left[1+2 \cdot \sin(36^\circ)\right]\hspace{0.15 cm}\underline{={{\rm 2.176 \hspace{0.05cm} V}}},$$

$$s_{\rm TP}(t = {\rm 25 \hspace{0.05cm} \mu s}) = {\rm 1 \hspace{0.05cm} V} \cdot \left[1+2 \cdot \sin(90^\circ)\right]\hspace{0.15 cm}\underline{={{\rm 3 \hspace{0.05cm} V}}},$$

$$s_{\rm TP}(t = {\rm 75 \hspace{0.05cm} \mu s}) = {\rm 1 \hspace{0.05cm} V} \cdot \left[1+2 \cdot \sin(270^\circ)\right]\hspace{0.15 cm}\underline{= -{{\rm 1 \hspace{0.05cm} V}}},$$

$$s_{\rm TP}(t = {\rm 100 \hspace{0.05cm} \mu s}) = s_{\rm TP}(t = 0) \hspace{0.15 cm}\underline{={{\rm 1 \hspace{0.05cm} V}}}.$$

3. Definitionsgemäß gilt $a(t) = |s_{TP}(t)|$. Damit erhält man folgende Zahlenwerte:

$$a(t = {\rm 25 \hspace{0.05cm} \mu s}) = s_{\rm TP}(t = {\rm 25 \hspace{0.05cm} \mu s}) \hspace{0.15 cm}\underline{= {\rm 3 \hspace{0.05cm} V}} , \hspace{4.15 cm}$$

$$a(t = {\rm 75 \hspace{0.05cm} \mu s}) = |s_{\rm TP}(t = {\rm 75 \hspace{0.05cm} \mu s})| \hspace{0.15 cm}\underline{= {\rm 1 \hspace{0.05cm} V}} .$$

4. Aufgrund der Tatsache, dass für alle Zeiten Im[ $s_{TP}(t)$ ] = 0 ist, erhält man aus der Beziehung

$$\phi(t)= {\rm arc} \left[s_{\rm TP}(t)\right]= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\left[s_{\rm TP}(t)\right]}{{\rm Re}\left[s_{\rm TP}(t)\right]}$$

das Ergebnis $\Phi(t)$ = 0, falls Re[ $s_{TP}(t)$ ] positiv ist, und $\Phi(t) = \pi$ bei negativem Realteil. Wir beschränken uns hier auf den Zeitbereich einer Periode: $0 \leq t \leq T_0$. Im Bereich zwischen $t_1$ und $t_2$ liegt eine Phase von 180° vor, ansonsten gilt $\text{Re}[s_{TP}(t)] \geq 0$. Zur Berechung von $t_1$ kann das Ergebnis aus 2) herangezogen werden:

$$\sin(2 \pi \cdot \frac{t_1}{T_0}) = -0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2 \pi \cdot \frac{t_1}{T_0} = 2 \pi \cdot \frac{7}{12}\hspace{0.3cm}{\rm (entspricht}\hspace{0.1cm}210^\circ )$$

Daraus erhält man $t_1$ = 7/12 · $T_0$ = 58.33 μs. Durch ähnliche Überlegungen kommt man zum Ergebnis $t_2$ = 11/12 · $T_0$ = 91.67 μs. Die gesuchten Werte sind somit $\Phi(t =$ 25 μs) = 0 und $\Phi(t = $75 μs) = 180° (= $\pi$).