Examples of Binary Block Codes

Single Parity–check Codes

Der Single Parity–check Code (SPC) fügt zu dem Informationsblock $\underline{u}= (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ ein Prüfbit (englisch: Parity) $p$ hinzu:

\[\underline{u} = (u_1, u_2,\hspace{0.05cm} ... \hspace{0.05cm} , u_k) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x} = (x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm} , x_n) = (u_1, u_2,\hspace{0.05cm} \text{...}\hspace{0.05cm} , u_k, p) \hspace{0.05cm}.\]

Single Parity–check Code $(n = k + 1)$

Die Grafik zeigt drei Coder–Beispiele mit

$|\mathcal{C}| = 4 \ (k = 2)$,
$|\mathcal{C}| = 8 \ (k = 3)$ und
$|\mathcal{C}| = 16 \ (k = 4)$.

Dieser sehr einfache Code ist wie folgt charakterisiert:

Aus $n = k + 1$ folgt für die Coderate $R = k/n = (n-1)/n$ und für die Redundanz $1-R = 1/n$. Für $k = 2$ ergibt sich zum Beispiel die Coderate 2/3 und die relative Redundanz beträgt 33.3%.

Das Prüfbit erhält man durch die Modulo–2–Addition. Darunter versteht man die Addition im Galoisfeld zur Basis 2 ⇒ GF(2), sodass $1 \oplus 1 = 0$ ergibt:

\[p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k \hspace{0.05cm}.\]

Damit enthält jedes gültige Codewort $\underline{x}$ eine gerade Anzahl von Einsen. Ausgedrückt mit $\oplus$ bzw. in vereinfachter Schreibweise entsprechend der zweiten Gleichung lautet diese Bedingung:

\[ x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 \hspace{0.05cm}, \hspace{0.5cm}{\rm oder:}\hspace{0.15cm} \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} , \hspace{0.3cm} {\rm Addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} \hspace{0.05cm}. \]

Für $k = 2$ ⇒ $n = 3$ ergeben sich die folgenden vier Codeworte, wobei in der ersten Zeile das Prüfbit jeweils durch einen kleinen Pfeil markiert ist:

\[\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\]

Es handelt sich um einen linearen Code, da die Summe zweier beliebiger Codeworte wieder ein gültiges Codewort ergibt, zum Beispiel :$$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$

Für beliebiges $k$ ⇒ $n = k+1$ unterscheidet sich jedes Codewort von allen anderen an einer geraden Anzahl von Positionen. Bei diesem Code ist die minimale Distanz $d_{\rm min} = 2$.

$\text{Definition:}$ Jeder Single Parity–check Code (SPC) lässt sich formal wie folgt beschreiben:

\[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm mit \hspace{0.15cm}geradzahliger\hspace{0.15cm} Anzahl\hspace{0.15cm} von\hspace{0.15cm} Einsen\hspace{0.15cm} in \hspace{0.15cm} } \underline{x} \}\hspace{0.05cm}.\]

Mit der allgemeinen Codebezeichnung $(n, k, d_{\rm min})$ lässt sich jeder Single Parity–check Code auch mit $(n, n-1, 2)$ benennen.
Die obere Grafik zeigt somit den SPC (3, 2, 2), den SPC (4, 3, 2) und den SPC (5, 4, 2).

Der digitale Kanal ändert möglicherweise das Codewort $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$ in das Empfangswort $\underline{y}= (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$, wobei mit dem Fehlervektor $\underline{e}= (e_1, e_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, e_n)$ gilt:

$$\underline{y}= \underline{x} \oplus \underline{e}.$$

Zur Decodierung des Single Parity–check Codes bildet man das so genannte Syndrom:

\[s = y_1 \oplus y_2 \oplus ... \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} \hspace{0.05cm}.\]

Das Ergebnis $s=1$ weist dann auf (mindestens) einen Bitfehler innerhalb des Codewortes hin, während $s=0$ wie folgt zu interpretieren ist:

Die Übertragung war fehlerfrei, oder:
Die Anzahl der Bitfehler ist geradzahlig.

Mögliche Empfangswerte beim SPC (4, 3, 2)

$\text{Beispiel 1:}$ Wir betrachten den SPC (4, 3, 2) und gehen davon aus, dass das Nullwort gesendet wurde.

Die Tabelle zeigt alle Möglichkeiten, dass $f$ Bit verfälscht werden und gibt das jeweilige Syndrom $s \in \{0, 1\}$ an.
Für das BSC–Modell mit der Verfälschungswahrscheinlichkeit $\varepsilon = 1\%$ ergeben sich dann folgende Wahrscheinlichkeiten:

Das Informationswort wird richtig decodiert (blaue Hinterlegung):

\[{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.\]

Der Decoder erkennt, dass Übertragungsfehler aufgetreten sind (grüne Hinterlegung):

\[{\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm ungerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.\]

Das Informationswort wird falsch decodiert (rote Hinterlegung):

\[{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.\]

Wir verweisen hier auf das interaktive Applet Ereigniswahrscheinlichkeiten der Binomialverteilung. Die hier gewonnenen Ergebnisse werden auch in der Aufgabe A1.5 nochmals diskutiert.

Single Parity–check Codes (3)

Eine Fehlerkorrektur des Single Parity–check Codes ist beim BSC–Modell nicht möglich im Unterschied zum BEC–Kanal (Binary Erasure Channel). Bei diesem werden Bitfehler ausgeschlossen. Ist nur ein Bit ausgelöscht (englisch: Erasure, E), so ist aufgrund der Tatsache „die Anzahl der Einsen im Codewort ist gerade” auch eine Fehlerkorrektur möglich, zum Beispiel für den SPC (5, 4):

\[\underline{y} \hspace{-0.1cm} = \hspace{-0.1cm} (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (1, 0, 1, 1) = \underline{u}\hspace{0.05cm},\] \[\underline{y} \hspace{-0.1cm} = \hspace{-0.1cm} (0, 1, 1, {\rm E}, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 1, 0, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 1, 0) = \underline{u}\hspace{0.05cm},\] \[\underline{y} \hspace{-0.1cm} = \hspace{-0.1cm} (0, 1, 0, 1, {\rm E}) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 0, 1, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 0, 1) = \underline{u}\hspace{0.05cm}.\]

Auch beim AWGN–Kanal ist Fehlerkorrektur möglich, wenn man Soft Decision anwendet. Für das Folgende gehen wir von bipolarer Signalisierung aus: x = 0 → x̃ = +1, x = 1 → x̃ = –1.

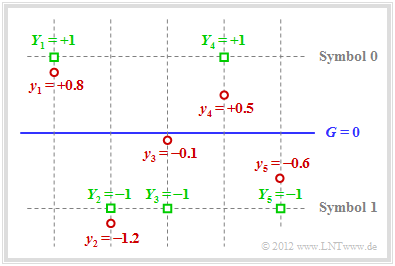
Zur Verdeutlichung von Soft Decision bei AWGN

Die Grafik verdeutlicht den hier dargelegten Sachverhalt:

Beispielsweise lautet der Empfangsvektor (rote Punkte):

\[\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.\]

Bei harter Entscheidung (Schwelle G = 0, nur die Vorzeichen werden ausgewertet) würde man zu folgendem binären Ergebnis kommen (grüne Quadrate Y_i = y_i / |y_i|):

\[\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.\]

In Symbolschreibweise ergibt sich daraus (0, 1, 1, 0, 1), was kein gültiges Codewort ist ⇒ Syndrom s = 1. Also müssen ein, drei oder fünf Bit verfälscht worden sein.

Die Wahrscheinlichkeit für drei oder fünf Bitfehler ist allerdings um Größenordnungen kleiner als diejenige für einen einzigen Fehler. Die Annahme „ein Bitfehler” ist deshalb nicht abwegig.

Da der Empfangswert y₃ sehr nahe an der Schwelle G = 0 liegt, geht man davon aus, dass genau dieses Bit verfälscht wurde. Damit fällt bei Soft Decision die Entscheidung für z = (0, 1, 0, 0, 1) ⇒ υ = (0, 1, 0, 0). Die Blockfehlerwahrscheinlichkeit Pr(υ ≠ u) ist so am geringsten.

Wiederholungscodes

: Man bezeichnet einen linearen binären (n, k)–Blockcode

\[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n): x_i = x_j \hspace{0.15cm}{\rm f\ddot{u}r \hspace{0.15cm}alle\hspace{0.25cm}} i, j = 1, ... \hspace{0.1cm}, n \}\]

als Wiederholungscode (englisch: Repetition Code, RC) der Länge n. Es gilt also stets k = 1. Entsprechend existieren nur zwei Codeworte (0, 0, ... , 0) und (1, 1, ... , 1), die sich in n Binärstellen unterscheiden. Daraus folgt für die minimale Distanz d_min = n.

Ein solcher (n, 1, n)–Blockcode besitzt nur die sehr kleine Coderate R = 1/n, ist aber auch sehr robust. Insbesondere beim BEC–Kanal genügt ein einziges richtig übertragenes Bit an beliebiger Position (alle anderen Bit können ausgelöscht sein), um das Informationswort richtig zu decodieren.

Wiederholungscode (Repetition Code)

Betrachten wir zunächst die Decodierung und Fehlerwahrscheinlichkeiten beim BSC–Kanal.

: Es gelte der BSC–Kanal mit ε = 10%. Die Decodierung basiere auf dem Majoritätsprinzip. Bei ungeradem n können e = n – 1 Fehler erkannt und t = (n – 1)/2 Bitfehler korrigiert werden. Damit ergibt sich für die Wahrscheinlichkeit der korrekten Decodierung der Informationsbits u:

\[{\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.\]

Die nachfolgenden Zahlenwerte gelten für n = 5. Das heißt: Es sind t = 2 Bitfehler korrigierbar:

\[{\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%\]

\[\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.\]

Bei geradem n können dagegen nur n/2 – 1 Fehler korrigiert werden. Erhöht man n von 5 auf 6, so sind weiterhin auch nur zwei Bitfehler innerhalb eines Codewortes korrigierbar. Einen dritten Bitfehler kann man zwar nicht korrigieren, aber zumindest erkennen:

\[{\rm Pr}({\rm nicht\hspace{0.15cm} korrigierbarer\hspace{0.15cm} Fehler}) = {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx 1.46\,\%\hspace{0.05cm}. \]

Ein (unerkannter) Decodierfehler (υ ≠ u) ergibt sich erst, wenn innerhalb des 6 Bit–Wortes vier oder mehr Bit verfälscht wurden. Als Näherung unter der Annahme, dass fünf oder sechs Bitfehler sehr viel unwahrscheinlicher sind als vier, gilt:

\[{\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= 0.122\,\%\hspace{0.05cm}.\]

Interessant ist, dass beim RC(6, 1, 6) die Wahrscheinlichkeit Pr(υ = u) für eine mögliche und richtige Decodierung mit 98.42% kleiner ist als beim RC(5, 1, 5).

Wiederholungscodes (2)

Nun interessieren wir uns für die Leistungsfähigkeit des Wiederholungscodes beim AWGN–Kanal. Bei uncodierter Übertragung (oder dem Wiederholungscode mit n = 1) ist der Empfangswert y = x̃ + η, wobei x̃ ∈ {+1, –1} das Informationsbit bei bipolarer Signalisierung bezeichnet und η den Rauschterm. Um Verwechslungen mit dem Codeparameter n zu vermeiden, wurde das Rauschen umbenannt: n → η.

Für die Fehlerwahrscheinlichkeit gilt mit dem Komplementären Gaußschen Fehlerintegral Please add link and do not upload flash videos. Q(x)

\[{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) \hspace{0.05cm},\]

wobei folgende physikalische Größen zu verwenden sind:

das Signal–zu–Rauschleistungsverhältnis ρ = 1/σ² = 2 E_S/N₀,

die Energie E_S pro Codesymbol ⇒ Symbolenergie,

die normierte Streuung σ des Rauschens, gültig für das Nutzsignal x̃ ∈ {+1, –1}, und

die konstante (einseitige) Rauschleistungsdichte N₀ des AWGN–Rauschens.

Bei einem (n, 1, n)–Wiederholungscode ergibt sich dagegen für den Eingangswert des ML–Decoders y' = x̃' + η' mit folgenden Eigenschaften:

\[\tilde{x} \hspace{0.04cm}' \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Amplitude} \hspace{0.2cm} \Rightarrow\hspace{0.2cm}n^2{\rm -fache \hspace{0.15cm}Leistung}\hspace{0.05cm},\] \[\eta\hspace{0.04cm}' \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Varianz:\hspace{0.15cm}} \sigma^2 \rightarrow n \cdot \sigma^2\hspace{0.05cm},\] \[\rho\hspace{0.04cm}' \hspace{-0.1cm} = \hspace{-0.1cm} \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho \hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S}}{N_0}})\hspace{0.05cm}.\]

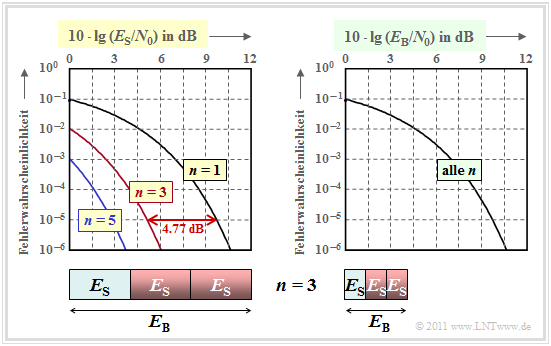
Die linke Grafik zeigt die Fehlerwahrscheinlichkeit in doppelt logarithmischer Darstellung. Als Abszisse ist 10 · lg (E_S/N₀) aufgetragen. Die Bildbeschreibung folgt auf der nächsten Seite.

Fehlerwahrscheinlichkeit des Wiederholungscodes beim AWGN–Kanal

Wiederholungscodes (3)

Es folgt nun die Interpretation der angegebenen Grafiken.

Die linke Grafik kann wie folgt interpretiert werden:

Trägt man die Fehlerwahrscheinlichkeit über der Abszisse 10 · lg (E_S/N₀) auf, so ergibt sich durch n–fache Wiederholung gegenüber uncodierter Übertragung (n = 1) eine signifikante Verbesserung.

Die Kurve für den Wiederholungsfaktor n erhält man durch Linksverschiebung um 10 · lg n (in dB) gegenüber der Vergleichskurve. Der Gewinn beträgt 4.77 dB (n = 3) bzw. ca. 7 dB (n = 5).

Allerdings ist ein Vergleich bei konstantem E_S nicht fair, da man mit einem (5, 1) Repetition Code für die Übertragung eines Informationsbits eine um den Faktor n größere Energie aufwendet:

\[E_{\rm B} = \frac{E_{\rm S}}{R} = n \cdot E_{\rm S} \hspace{0.05cm}.\]

Aus der rechten Grafik erkennt man, dass alle Kurven genau übereinander liegen, wenn auf der Abszisse 10 · lg (E_B/N₀) aufgetragen wird. Daraus folgt:

Zusammenfassung der Ergebnisse für den Wiederholungscode bei AWGN

Die Fehlerwahrscheinlichkeit ist bei fairem Vergleich unabhängig vom Wiederholungsfaktor n:

\[{\rm Pr}(v \ne u) = {\rm Q}\left (\sqrt{\frac{2E_{\rm B}}{N_0}} \right ) \hspace{0.05cm}.\]

Beim AWGN–Kanal ist durch einen Wiederholungscode kein Codiergewinn zu erzielen.

Hamming–Codes (1)

Richard Wesley Hamming hat 1962 eine Klasse binärer Blockcodes angegeben, die sich durch die Anzahl m = 2, 3, ... der zugesetzten Parity Bits unterscheiden. Für diese Codeklasse gilt:

Die Codelänge ergibt sich zu n = 2^m – 1. Möglich sind demzufolge beim Hamming–Code nur die Längen n = 3, n = 7, n = 15, n = 31, n = 63, n = 127, n = 255, usw.

Ein Informationswort besteht aus k = n – m Bit. Die Coderate ist somit gleich

\[R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, \hspace{0.1cm}120/127,\hspace{0.1cm}247/255, \hspace{0.05cm} ... \hspace{0.05cm} \}\hspace{0.05cm}.\]

Alle Hamming–Codes weisen die minimale Distanz d_min = 3 auf. Bei größerer Codelänge n erreicht man die minimale Distanz 3 schon mit weniger Redundanz, also bei größerer Coderate R.

Aus der Angabe d_min = 3 folgt weiter, dass hier e = d_min – 1 = 2 Fehler erkannt werden können und t = (d_min – 1)/2 = 1 Fehler korrigiert werden kann.

Der Hamming–Code (3, 1, 3) ist identisch mit dem Wiederholungscode (3, 1, 3):

\[\mathcal{C} = \{ (0, 0, 0) \hspace{0.05cm}, (1, 1, 1) \}\hspace{0.05cm}. \]

Bei systematischer Codierung sind die ersten k Stellen eines jeden Codewortes identisch mit dem Informationswort. Anschließend folgen bei einem Hamming–Code die m = n – k Paritätsbit:

\[\underline{x} = ( x_1, x_2, ... \hspace{0.05cm}, x_n) = ( u_1, u_2, ... \hspace{0.05cm}, u_k, p_1, p_2, ... \hspace{0.05cm}, p_{n-k}) \hspace{0.05cm}.\]

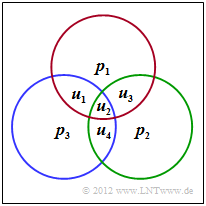
Im Folgenden betrachten wir stets den (7, 4, 3)–Hamming–Code, der durch das folgende Schaubild verdeutlicht wird. Daraus lassen sich die drei Bedingungen ableiten:

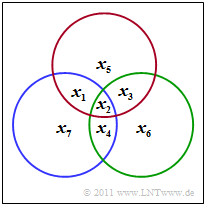\[x_1 \oplus x_2 \oplus x_3 \oplus x_5 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\] \[x_2 \oplus x_3 \oplus x_4 \oplus x_6 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\] \[x_1 \oplus x_2 \oplus x_4 \oplus x_7 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm}. \]

Im Schaubild kennzeichnet der rote Kreis die erste Prüfgleichung, der grüne die zweite und der blaue die letzte. In jedem Kreis muss die Anzahl der Einsen geradzahlig sein.

Hamming–Codes (2)

Bei systematischer Codierung des (7, 4, 3)–Hamming–Codes

\[x_1 \hspace{-0.2cm} = \hspace{-0.2cm} u_1 ,\hspace{0.2cm} x_2 = u_2 ,\hspace{0.2cm} x_3 = u_3 ,\hspace{0.2cm} x_4 = u_4 ,\hspace{0.2cm}\] \[x_5 \hspace{-0.2cm} = \hspace{-0.2cm} p_1 ,\hspace{0.2cm} x_6 = p_2 ,\hspace{0.2cm} x_7 = p_3 \]

lauten die Bestimmungsgleichungen der drei Prüfbit, wie aus dem Schaubild rechts hervorgeht:

\[p_1 \hspace{-0.1cm} = \hspace{-0.1cm} u_1 \oplus u_2 \oplus u_3 \hspace{0.05cm},\] \[p_2 \hspace{-0.1cm} = \hspace{-0.1cm} u_2 \oplus u_3 \oplus u_4 \hspace{0.05cm},\] \[p_3 \hspace{-0.1cm} = \hspace{-0.1cm} u_1 \oplus u_2 \oplus u_4 \hspace{0.05cm}.\]

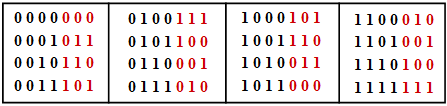
Die nachfolgende Tabelle zeigt die 2^k = 16 zulässigen Codeworte x = (u₁, u₂, u₃, u₄, p₁, p₂, p₃) des systematischen (7, 4, 3)–Codes. Das Informationswort u = (u₁, u₂, u₃, u₄) ist schwarz dargestellt und die Prüfbits p₁, p₂, p₃ rot. Man erkennt anhand dieser Tabelle, dass sich jeweils zwei der 16 möglichen Codeworte in mindestens d_min = 3 Binärwerten unterscheiden.

Zuordnung u → x des systematischen (7, 4, 3)–Hamming–Codes

Die Decodierung linearer Blockcodes wird im Kapitel 1.5 ausführlich behandelt. Das nun folgende Beispiel soll die Decodierung des Hamming–Codes eher intuitiv erklären.

: Wir gehen vom systematischen (7, 4, 3)–Code aus und betrachten das Empfangswort y = (y₁, y₂, y₃, y₄, y₅, y₆, y₇). Zur Decodierung bilden wir die drei Paritätsgleichungen

\[ y_1 \oplus y_2 \oplus y_3 \oplus y_5 \hspace{-0.1cm}= \hspace{-0.1cm} 0 \hspace{0.05cm},\hspace{0.5cm}{\rm (I)} \] \[y_2 \oplus y_3 \oplus y_4 \oplus y_6 \hspace{-0.1cm}= \hspace{-0.1cm}0 \hspace{0.05cm},\hspace{0.5cm}{\rm (II)} \] \[y_1 \oplus y_2 \oplus y_4 \oplus y_7 \hspace{-0.1cm}= \hspace{-0.1cm} 0\hspace{0.05cm}. \hspace{0.5cm}{\rm (III)}\]

Unter der Voraussetzung, dass in jedem Codewort höchstens ein Bit verfälscht wird, gelten dann die folgenden Aussagen. υ bezeichnet das Decodierergebnis und sollte mit u = (1, 0, 1, 0) übereinstimmen:

Das Empfangswort y = (1, 0, 1, 0, 0, 1, 1) erfüllt alle drei Paritätsgleichungen. Das heißt, dass kein einziger Übertragungsfehler aufgetreten ist ⇒ y = x ⇒ u = (1, 0, 1, 0).

Werden zwei der drei Paritätsgleichungen erfüllt wie zum Beispiel für das empfangene Wort y = (1, 0, 1, 0, 0, 1, 0), so wurde ein Paritätsbit verfälscht und es gilt auch hier υ = (1, 0, 1, 0).

Mit y = (1, 0, 1, 1, 0, 1, 1) wird nur die Gleichung (I) erfüllt und die beiden anderen nicht. Somit kann man die Verfälschung des vierten Binärsymbols korrigieren, und es gilt auch hier υ = u.

Ein Übertragungsfehler des zweiten Bits ⇒ y = (1, 1, 1, 0, 0, 1, 1) führt dazu, dass alle drei Paritätsgleichungen nicht erfüllt werden. Auch dieser Fehler lässt sich eindeutig korrigieren.

Aufgaben

A1.5 SPC (5, 4) und BEC–Modell

Zusatzaufgaben:1.5 SPC (5, 4) vs. RC (5, 1)

A1.6 Zum (7, 4)–Hamming–Code