Exercise 3.09Z: Viterbi Algorithm again

• Return to book

Trellis für einen Rate–1/2–Code mit Gedächtnis $m = 1$

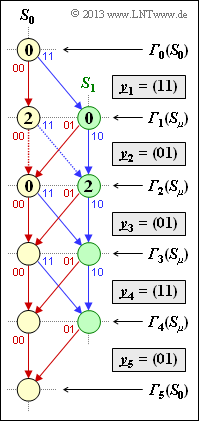
Die Grafik zeigt das Trellisdiagramm das Faltungscodes entsprechend Aufgabe A3.6, gekennzeichnet durch folgende Größen:

• Rate 1/2  ⇒  $k = 1, \ n = 2$,
• Gedächtnis $m = 1$,
• Übertragungsfunktionsmatrix $\mathbf{G}(D) = (1, \ 1 + D)$,
• Länge der Informationssequenz: $L = 4$,
• Sequenzlänge inclusive Terminierung: $L' = L + m = 5$.

Anhand dieser Darstellung soll die Viterbi–Decodierung schrittweise nachvollzogen werde, wobei von der folgenden Empfangssequenz auszugehen ist: $\underline{y} = (11, \, 01, \, 01, \, 11, \, 01)$.

In das Trellis eingezeichnet sind:

• Der Initialwert ${\it \Gamma}_0(S_0)$ für den Viterbi–Algorithmus wird stets zu $0$ gewählt.
• Die beiden Fehlergrößen für den ersten Decodierschritt $(i = 1)$ erhält man mit $\underline{y}_1 = (11)$ wie folgt:

$${\it \Gamma}_1(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 2 \hspace{0.05cm},$$

$${\it \Gamma}_1(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 0 \hspace{0.05cm}.$$

• Die Fehlergrößen zum Schritt $i = 2$  ⇒  $\underline{y}_2 = (01)$ egeben sich durch folgende Vergleiche:

$${\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] =$$

$$\ = \ \hspace{-0.15cm} {\rm min} \left [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+0 \right ] = 0\hspace{0.05cm},$$

$${\it \Gamma}_2(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] =$$

$$\ = \ \hspace{-0.15cm} {\rm min} \left [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+2 \right ] = 2\hspace{0.05cm}.$$

Fragebogen

1

Multiple-Choice

	correct
	false

2

Input-Box Frage

$xyz \ = \ $ $ab$

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)