Exercise 1.16: Block Error Probability Bounds for AWGN

Fehlerfunktion

${\rm Q}(x)$ und Näherungen

Wir gehen von der folgenden Konstellation aus:

ein linearer Blockcode mit Coderate $R = k/n$ und Distanzspektrum $\{W_i\}, \ i = 1, \ \text{...} \ , n$ ,
ein AWGN–Kanal, gekennzeichnet durch $E_{\rm B}/N_{0}$ ⇒ umrechenbar in die Rauschleistung $\sigma^2$ ,
ein Empfänger, basierend auf Soft Decision sowie dem Maximum–Likelihood–Kriterium.

Unter der für die gesamte Aufgabe gültigen Annahme, dass stets das Nullwort $\underline{x}_{1} = (0, 0, \text{...} \ , 0)$ gesendet wird, gilt für die „paarweise Fehlerwahrscheinlichkeit” mit einem anderen Codewort $\underline{x}_{l} (l = 2,\ \text{...} \ , 2^k)$ :

${\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = {\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm}.$

Die Herleitung dieser Beziehung finden Sie in [Liv10]. In dieser Gleichung werden verwendet:

die komplementäre Gaußsche Fehlerfunktion ${\rm Q}(x)$ ,
das Hamming–Gewicht $w_{\rm H}(\underline{x}_{l})$ des Codewortes $\underline{x}_{l}$ ,
die AWGN–Rauschleistung $\sigma^2 = (2 · R · E_{\rm B}/N_{0})^{–1}.$

Damit lassen sich verschiedene Schranken für die Blockfehlerwahrscheinlichkeit angeben:

die so genannte Union Bound (UB):

$p_1 = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = \sum_{l \hspace{0.05cm}= \hspace{0.05cm}2}^{2^k}\hspace{0.05cm}{\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm},$

die so genannte Truncated Union Bound (TUB):

$p_2 = W_{d_{\rm min}} \cdot {\rm Q}\left ( \sqrt{d_{\rm min}/\sigma^2} \right ) \hspace{0.05cm},$

die Bhattacharyya–Schranke:

$p_3 = W(\beta) - 1\hspace{0.05cm},\hspace{0.2cm} {\rm mit}\hspace{0.15cm} \beta = {\rm e}^{ - 1/(2\sigma^2) } \hspace{0.05cm}.$

In diesem Fall ist das Distanzspektrum

$\{W_i\}$ durch die Gewichtsfunktion zu ersetzen:

$\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot X^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.$

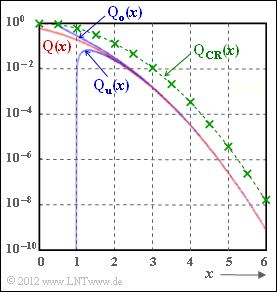
Beim Übergang von der Union Bound $p_{1}$ zur ungenaueren Schranke $p_{3}$ wird unter Anderem die Funktion ${\rm Q}(x)$ durch die Chernoff–Rubin–Schranke ${\rm Q}_{\rm CR}(x)$ ersetzt. Beide Funktionen sind in obigerer Grafik dargestellt (rote bzw. grüne Kurve).

In der Aufgabe 1.16Z wird der Zusammenhang zwischen diesen Funktionen numerisch ausgewertet und zu den Schranken ${\rm Q}_{o}(x)$ und ${\rm Q}_{u}(x)$ Bezug genommen, die in obiger Grafik ebenfalls eingezeichnet sind.

Hinweise:

Die Aufgabe gehört zum Kapitel Schranken für die Blockfehlerwahrscheinlichkeit.
Die oben zitierte Literaturstelle [Liv10] verweist auf das Vorlesungsmanuskript „Liva, G.: Channel Coding. Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2010.”
Weiter verweisen wir auf das interaktive Applet Komplementäre Gaußsche Fehlerfunktionen.

Fragebogen

	$p_{1} = \sum_{l\hspace{0.05cm}=\hspace{0.05cm}2}^{2^k} W_{l} · {\rm Q}\big[(l/\sigma^2)^{0.5}\big],$
	$p_{1} = \sum_{i\hspace{0.05cm}=\hspace{0.05cm}1}^{n} W_{i} · {\rm Q}\big[(i/\sigma^2)^{0.5}\big].$

$\sigma = 1.0 \text{:} \hspace{0.4cm} p_{1} \ = \$

$\ \%$

$\sigma = 0.5 \text{:} \hspace{0.4cm} p_{1} \ = \$

$\ \%$

$\sigma = 1.0 \text{:} \hspace{0.4cm} p_{2} \ = \$

$\ \%$

$\sigma = 0.5 \text{:} \hspace{0.4cm} p_{2} \ = \$

$\ \%$

	Die Blockfehlerwahrscheinlichkeit ist nie größer als $p_{1}$ .
	Die Blockfehlerwahrscheinlichkeit ist nie größer als $p_{2}$ .

	die Fehlerfunktion ${\rm Q}(x)$ durch die Funktion ${\rm Q}_{\rm CR}(x)$ ersetzt,
	den Bhattacharyya–Parameter $\beta = 1/\sigma$ setzt,
	statt $\{W_i\}$ die Gewichtsfunktion $W(X)$ verwendet.

$\sigma = 1.0 \text{:} \hspace{0.4cm} p_{3} \ = \$

$\ \%$

$\sigma = 0.5 \text{:} \hspace{0.4cm} p_{3} \ = \$

$\ \%$

Musterlösung

Solution

(1) Richtig ist die Antwort 2. Das Distanzspektrum

$\{W_i\}$ ist definiert für

$i = 0, \ \text{...} \ , \ n$ :

$W_{1}$ gibt an, wie oft das Hamming–Gewicht $w_{\rm H}(\underline{x}_{i}) = 1$ auftritt.
$W_{n}$ gibt an, wie oft das Hamming–Gewicht $w_{\rm H}(\underline{x}_{i}) = n$ auftritt.

Damit lautet die Union Bound:

$p_1 = {\rm Pr(Union \hspace{0.15cm}Bound)}= \sum_{i = 1}^{n}\hspace{0.05cm}W_i \cdot {\rm Q}\left ( \sqrt{i/\sigma^2} \right ) \hspace{0.05cm}.$

(2) Das Distanzspektrum des $(8, 4, 4)$ –Codes wurde mit $W_{0} = 1 , \ W_{4} = 14, \ W_{8} = 1$ angegeben. Somit erhält man für $\sigma = 1$ :

$p_1 = W_4 \cdot {\rm Q}\left ( 2 \right ) + W_8 \cdot {\rm Q}\left ( 2 \cdot \sqrt{2} \right ) = 14 \cdot 2.28 \cdot 10^{-2}+ 1 \cdot 0.23 \cdot 10^{-2} \hspace{0.15cm}\underline{\approx 32.15\%}\hspace{0.05cm},$

bzw. für $\sigma = 0.5$ :

$p_1 = 14 \cdot {\rm Q}\left ( 4 \right ) + {\rm Q}\left ( 4 \cdot \sqrt{2} \right ) = 14 \cdot 3.17 \cdot 10^{-5}+ 1.1 \cdot 10^{-8} \hspace{0.15cm}\underline{\approx 0.0444 \%}\hspace{0.05cm}.$

(3) Mit der Minimaldistanz $d_{\rm min} = 4$ erhält man:

$\sigma = 1.0\text{:} \hspace{0.4cm} p_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} W_4 \cdot {\rm Q}\left ( 2 \right ) \hspace{0.15cm}\underline{= 31.92\%}\hspace{0.05cm},$

$\sigma = 0.5\text{:} \hspace{0.4cm} p_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm}W_4 \cdot {\rm Q}\left ( 4 \right ) \approx p_1 \hspace{0.15cm}\underline{ = 0.0444 \%}\hspace{0.05cm}.$

(4) Richtig ist der Lösungsvorschlag 1:

Die Union Bound – hier mit $p_{1}$ bezeichnet – ist in jedem Fall eine obere Schranke für die Blockfehlerwahrscheinlichkeit.
Für die Schranke $p_{2}$ (Truncated Union Bound) trifft das nicht immer zu.
Beispielsweise erhält man beim $(7, 4, 3)$ –Hamming–Code ⇒ $W_{3} = W_{4} = 7, \ W_{7} = 1$ mit der Streuung $\sigma = 1$ :

$p_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 7 \cdot {\rm Q}\left ( \sqrt{3} \right ) = 7 \cdot 4.18 \cdot 10^{-2} \approx 0.293\hspace{0.05cm},$

$p_1 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} p_2 + 7 \cdot {\rm Q}\left ( \sqrt{4} \right )+ 1 \cdot {\rm Q}\left ( \sqrt{7} \right ) \approx 0.455 \hspace{0.05cm}.$

Die tatsächliche Blockfehlerwahrscheinlichkeit wird wahrscheinlich zwischen $p_{2} = 29.3\%$ und $p_{1} = 45.5\%$ liegen (wurde allerdings nicht nachgeprüft). Das heißt: $p_{2}$ ist keine obere Schranke.

(5) Richtig sind die Lösungsvorschläge 1 und 3, wie die folgende Rechnung für den $(8, 4, 4)$ –Code zeigt:

Es gilt ${\rm Q}(x) ≤ {\rm Q_{CR}}(x) = {\rm e}^{-x^2/2}$ . Damit kann für die Union Bound

$p_1 = W_4 \cdot {\rm Q}\left ( \sqrt{4/\sigma^2} \right ) +W_8 \cdot {\rm Q}\left ( \sqrt{8/\sigma^2} \right )$

eine weitere obere Schranke angegeben werden:

$p_1 \le W_4 \cdot {\rm e}^{ - {4}/(2 \sigma^2) } +W_8 \cdot {\rm e}^{ - {8}/(2 \sigma^2) } \hspace{0.05cm}.$

Mit $\beta = {\rm e}^{–1/(2\sigma^2)}$ kann hierfür auch geschrieben werden (das vorgegebene $\beta = 1/\sigma$ ist also falsch):

$p_1 \le W_4 \cdot \beta^4 + W_8 \cdot \beta^8 \hspace{0.05cm}.$

Die Gewichtsfunktion des $(8, 4, 4)$ –Codes lautet:

$W(X) = 1 + W_4 \cdot X^4 + W_8 \cdot X^8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W(\beta) - 1 = W_4 \cdot \beta^4 + W_8 \cdot \beta^8\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_3 = W(\beta) - 1 \ge p_1\hspace{0.05cm}.$

(6) Mit $\sigma = 1$ lautet der Bhattacharyya–Parameter $\beta = {\rm e}^{–0.5} = 0.6065$ und man erhält damit für die Bhattacharyya–Schranke:

$p_3 = 14 \cdot \beta^4 + \beta^8 = 14 \cdot 0.135 + 0.018= 1.913 \hspace{0.15cm}\underline{= 191.3%}\hspace{0.05cm}.$

Berücksichtigt man, dass $p_{3}$ (eine Schranke für) eine Wahrscheinlichkeit angibt, so ist $p_{3} = 1.913$ nur eine triviale Schranke. Für $\sigma = 0.5$ ergibt sich dagegen $\beta = {\rm e}^{–2} \approx 0.135.$ Dann gilt:

$p_3 = 14 \cdot \beta^4 + \beta^8 = 14 \cdot 3.35 \cdot 10^{-4} + 1.1 \cdot 10^{-7} \hspace{0.15cm}\underline{= 0.47 \%}\hspace{0.05cm}.$

Ein Vergleich mit der Teilaufgabe (2) zeigt, dass im vorliegenden Beispiel die Bhattacharyya–Schranke $p_{3}$ um den Faktor $(0.47 · 10^{–2})/(0.044 · 10^{–2}) > 10$ oberhalb der Union Bound $p_{1}$ liegt.

Der Grund für diese große Abweichung ist die Chernoff–Rubin–Schranke, die deutlich oberhalb der ${\rm Q}$ –Funktion liegt.
In der Aufgabe 1.16Z wird die Abweichung zwischen ${\rm Q}_{\rm CR}$ und ${\rm Q}(x)$ auch quantitativ berechnet:

${{\rm Q_{CR}}( x )}/{{\rm Q}( x )} \approx 2.5 \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {{\rm Q_{CR}}( x = 4 )}/{{\rm Q}( x = 4)} \approx 10 \hspace{0.05cm}.$