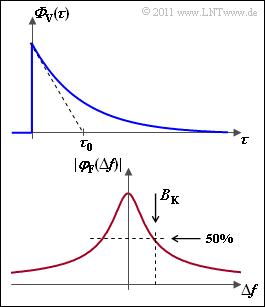
Exercise 2.7: Coherence Bandwidth

• Return to book

Verzögerungs–LDS und
Frequenz–Korrelationsfunktion

For the power spectral density of the delay, we assume an exponential behavior. With  ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$  we have

$${{\it \phi}_{\rm V}(\tau)}/{{\it \phi}_{\rm 0}} = {\rm e}^{ -\tau / \tau_0 } \hspace{0.05cm}.$$

The constant  $\tau_0$  can be determined from the tangent in the point  $\tau = 0$  according to the upper graph. Note that  ${\it \Phi}_{\rm V}(\tau)$  has dimension  $[1/\rm s]$ . Furthermore,

• The probability density function (PDF)  $f_{\rm V}(\tau)$  has the same form as  ${\it \Phi}_{\rm V}(\tau)$, but is normalized to area  $1$ .
• The  average excess delay or mean excess delay  $m_{\rm V}$  is equal to the linear expectation  $E\big [\tau \big]$  and can be determined from the PDF  $f_{\rm V}(\tau)$ .
• The  multipath spread or delay spread  $\sigma_{\rm V}$  gives the standard deviation (dispersion) of the random variable  $\tau$ . In the theory part we also use the term  $T_{\rm V}$ for this.
• The displayed frequency correlation function  $\varphi_{\rm F}(\delta f)$  can be calculated as the Fourier transform of the power spectral density of the delay  ${\it \Phi}_{\rm V}(\tau)$ :

$$\varphi_{\rm F}(\Delta f) \hspace{0.2cm} {\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} {\it \Phi}_{\rm V}(\tau)\hspace{0.05cm}.$$

• The coherence bandwidth  $B_{\rm K}$  is the value of   $\Delta f$ at which the frequency correlation function  $\varphi_{\rm F}(\Delta f)$  has dropped to half in absolute value.

Notes:

• This task belongs to the topic of the chapter  GWSSUS–Kanalmodell.
• This task requires knowledge of   computation of moments  of random variables from the book „Stochastic Signal Theory”.
• In addition, the following Fourier transform is given:

$$x(t) = \left\{ \begin{array}{c} {\rm e}^{- \lambda \hspace{0.05cm}\cdot \hspace{0.05cm} t}\\ 0 \end{array} \right.\quad \begin{array}{*{1}c} \hspace{-0.35cm} {\rm f\ddot{u}r} \hspace{0.15cm} t \ge 0 \\ \hspace{-0.35cm} {\rm f\ddot{u}r} \hspace{0.15cm} t < 0 \\ \end{array} \hspace{0.4cm} {\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet} \hspace{0.4cm} X(f) = \frac{1}{\lambda + {\rm j} \cdot 2\pi f}\hspace{0.05cm}.$$

Questionnaire

1

What is the probability density  $f_{\rm V}(\tau)$  of the delay?

	$f_{\rm V}(\tau) = {\rm e}^{-\tau/\tau_0}$.
	$f_{\rm V}(\rm e} = 1/\tau_0 \cdot ^{-\tau/\tau_0}$,
	$f_{\rm V}(\tau) = {\it \Phi}_0 \cdot {\rm e}^{-\tau/\tau_0}$.

2

Determine the average delay time for  $\tau_0 = 1 \ \ \rm µ s$.

$m_{\rm V} \ = \ $ $\ \rm µ s$

3

Which value results for the multipath widening with  $\tau_0 = 1 \ \ \rm µ s$?

$\sigma_{\rm V} \ = \ $ $\ \rm µ s$

4

What equation applies to the frequency–correlation function  $\varphi_{\rm F}(\delta f)$?

	$\varphi_{\rm F}(\Delta f) = \big[1/\tau_0 + {\rm j} \ 2 \pi \cdot \delta f \big]^{-1}$,
	$\varphi_{\rm F}(\Delta f) = {\rm e}^ {-(\tau_0 \hspace{0.05cm}\cdot \hspace{0.05cm}\Delta f)^2}$.

5

Determine the coherence bandwidth  $B_{\rm K}$.

$B_{\rm K} \ = \ $ $\ \ \rm kHz$

Sample solution

Solution

(1)  The integral over the power spectral density of the delay delivers with ${\it \Phi}_0 = {\it \Phi}_{\rm V}(\tau = 0)$ the result $$\int_{0}^{+\infty} {\it \Phi}_{\rm V}(\tau) \hspace{0.15cm}{\rm d} \tau = {\it \Phi}_{\rm 0} \cdot \int_{0}^{+\infty} {\rm e}^{-\tau / \tau_0} \hspace{0.15cm}{\rm d} \tau = {\it \Phi}_{\rm 0} \cdot \tau_0 \hspace{0.05cm}.$$

• This gives for the probability density function

$$f_{\rm V}(\tau) = \frac{{{\it \phi}_{\rm V}(\tau) }{{\it \phi}_{\rm 0} \cdot \tau_0}= \frac{1}{\frac{1}{\a_dot_0} \cdot {\rm e}^{-\tau / \tau_0} \hspace{0.05cm}.$$

• Solution 2 is therefore correct.

(2)  The $k$–te moment of a Exponential_Random_Size is equal to $m_k = k according to our nomenclature! \cdot \tau_0^k$.

• With $k = 1$ this results in the linear mean value $m_1 = m_{\rm V}$:

$$m_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm & micro; s} \hspace{0.05cm}. $$

(3)  According to the Steiner's Theorem, the following applies generally to the variance of a random variable: $\sigma^2 = m_2 \, –m_1^2$.

• According to the above equation, $m_2 = 2 \cdot \tau_0^2$. It follows:

$$\sigma_{\rm V}^2 = m_2 - m_1^2 = 2 \cdot \tau_0^2 - (\tau_0)^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma_{\rm V} = \tau_0 \hspace{0.1cm} \underline {= 1\,{\rm & micro; s} \hspace{0.05cm}. $$

(4)  ${\it \Phi}_{\rm V}(\tau)$ is identical to $x(t)$ given in the auxiliary equation if $t$ is replaced by $\tau$ and $\lambda$ by $1/\tau_0$.

• Thus $\varphi_{\rm F}(\delta f)$ has the same course as $X(f)$ with the substitution $f → \delta f$:

$$\varphi_{\rm F}(\delta f) = \frac{1}{1/\tau_0 + {\rm j} \cdot 2\pi \delta f} = \frac{\tau_0}{1 + {\rm j} \cdot 2\pi \cdot \tau_0 \cdot \delta f}\hspace{0.05cm}.$ *"Correct is the <u>first equation. '''(5)'''  The coherence bandwidth is implicit in the following equation:$$ $|\varphi_{\rm F}(\Delta f = B_{\rm K})| \stackrel {!}{=} \frac{1}{2} \cdot |\varphi_{\rm F}(\delta f = 0)| = \frac{\tau_0}{2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}|\varphi_{\rm F}(\Delta f = B_{\rm K})|^2 = \frac{\dot_0^2}{1 + (2\pi \cdot \dot_0 \cdot B_{\rm K})^2} \stackrel {!}{=} \frac{\tau_0^2}{4}'"`UNIQ-MathJax26-QINU`"'\Rightarrow \hspace{0.3cm}(2\pi \cdot \tau_0 \cdot B_{\rm K})^2 = 3 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} B_{\rm K}= \frac{\sqrt{3}}{2\pi \cdot \tau_0} \approx \frac{0.276}{ \tau_0}\hspace{0.05cm}.$

• With $\tau_0 = 1 \ \ \rm µ s$ follows for the coherence bandwidth $B_{\rm K} \ \underline {= 276 \ \ \rm kHz}$.