Generation of Walsh functions

Open Applet in new Tab

Program description

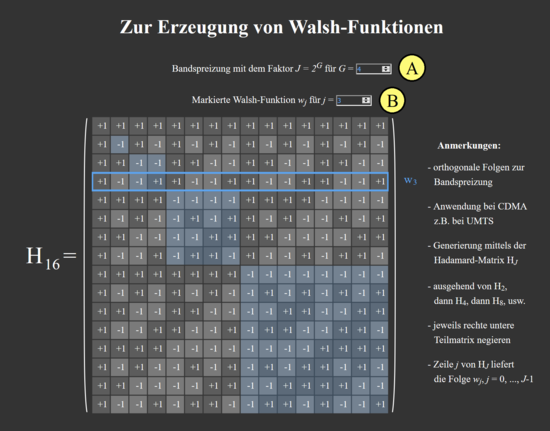
This applet allows to display the Hadamard matrices  $\mathbf{H}_J$  for the construction of the Walsh functions  $w_j$.  The factor  $J$  of the band spreading as well as the selection of the individual Walsh functions  (by blue bordering the rows of the matrix)  can be changed.

Theoretical background

Application

The  Walsh functions  are a group of periodic orthogonal functions.  Their application in digital signal processing is mainly in the use for band spreading in CDMA systems, for example the mobile radio standard UMTS.

• Due to their orthogonal properties and the favourable periodic cross-correlation function  $\rm (PCCF)$, the Walsh functions represent optimal spreading sequences for a distortion-free channel and a synchronous CDMA system.  If you take any two lines and form the correlation (averaging over the products), the PCCF value is always zero.
• In asynchronous operation  (example:   uplink of a mobile radio system)  or de-orthogonalization due to multipath propagation, Walsh functions alone are not necessarily suitable for band spreading.
• In terms of  $\rm (PACF)$  (periodic cross-correlation function) these sequences are less good:  Each individual Walsh function has a different PACF and each individual PACF is less good than a comparable pseudo noise  $\rm (PN)$  sequence. That means:   The synchronization is more difficult with Walsh functions than with PN sequences.

Construction

The construction of Walsh functions can be done recursively using the  Hadamard matrices.

• A Hadamard matrix  $\mathbf{H}_J$  of order  $J$  is a  $J\times J$  matrix, which contains line by line the  $\pm 1$  weights of the Walsh sequences.
• The orders of the Hadamard matrices are fixed to powers of two, i.e.  $J = 2^G$  applies to a natural number  $G$. Starting from $\mathbf{H}_1 = [+1]$ and

$$ \mathbf{H}_2 = \left[ \begin{array}{rr} +1 & +1\\ +1 & -1 \\ \end{array}\right] $$

the following relationship applies to the generation of further Hadamard matrices:

$$ \mathbf{H}_{2N} = \left[ \begin{array}{rr} +\mathbf{H}_N & +\mathbf{H}_N\\ +\mathbf{H}_N & -\mathbf{H}_N \\ \end{array}\right] $$

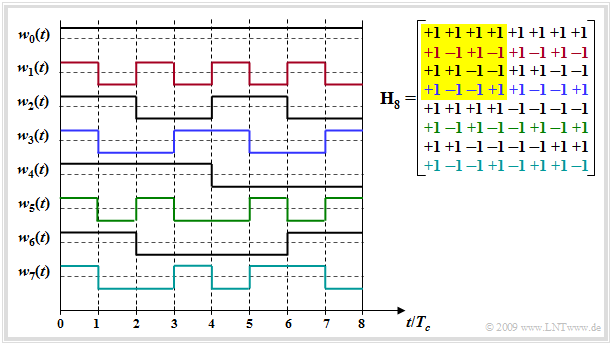
$\text{Example:}$  The graphic shows the Hadamard matrix  $\mathbf H_8$  (right) and the  $J -1$  spreading sequences which can be constructed with it.

Walsh spreading sequences  $(J = 8)$  and Hadamard matrix  $\mathbf H_8$ 

• $J - 1$ because the unspread sequence  $w_0(t)$  is usually not used.
• Please note the color assignment between the lines of the Hadamard matrix and the spreading sequences  $w_j(t)$.
• The matrix  $\mathbf H_4$  is highlighted in yellow.

}

How to use the applet

    (A)     Selection of the factor for band spreading as power of two of $G$

    (B)     Selection of the respective Walsh function $w_j$

About the authors

Dieses interaktive Berechnungstool wurde am  Lehrstuhl für Nachrichtentechnik  der  Technischen Universität München  konzipiert und realisiert.

• Die erste Version wurde 2007 von  Thomas Großer  im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer:  Günter Söder).
• 2018/2019 wurde das Programm von  Carolin Mirschina  (Ingenieurspraxis, Betreuer:  Tasnád Kernetzky ) auf „HTML5” umgesetzt und neu gestaltet.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Open Applet in new Tab Translated with www.DeepL.com/Translator (free version)