Exercise 4.4: Pointer Diagram for DSB-AM

Spektrum des analytischen Signals

We assume a cosine-shaped source signal $q(t)$ with

the amplitude $A_{\rm N} = 0.8 \ \text{V}$ and
the frequency $f_{\rm N}= 10 \ \text{kHz}$ .

The frequency conversion is done by means of Zweiseitenband–Amplitudenmodulation mit Träger.

The modulated signal $s(t)$ is with the (normalised) carrier $z(t) = \text{cos}(\omega_{\rm T} \cdot t)$ and the DC component $q_0 = 1 \ \text{V}$ :

$\begin{align*} s(t) & = \left(q_0 + q(t)\right) \cdot z(t)= \left({\rm 1 \hspace{0.05cm} V} + {\rm 0.8 \hspace{0.05cm}V}\cdot {\cos} ( \omega_{\rm N}\cdot t)\right) \cdot {\cos} ( \omega_{\rm T}\cdot t) = \\ & = q_0 \cdot {\cos} ( \omega_{\rm T}\cdot t) + {A_{\rm N}}/{2} \cdot {\cos} ( (\omega_{\rm T}+ \omega_{\rm N}) \cdot t) + {A_{\rm N}}/{2} \cdot {\cos} ( (\omega_{\rm T}- \omega_{\rm N}) \cdot t).\end{align*}$

The first term describes the carrier, the second term the so-called upper sideband (USB) and the last term the lower sideband (LSB).

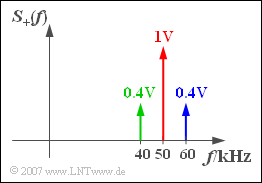
The sketch shows the spectrum $S_+(f)$ of the corresponding analytical signal for $f_{\rm T} = 50 \ \text{kHz}$ . You can see

the carrier (red),
the upper sideband (blue) and
the lower sideband (grün).

In subtask (5) the magnitude of $s_+(t)$ is asked for. This is the length of the resulting pointer.

Hints:

This task belongs to the chapter Analytical Signal and Its Spectral Function.

You can check your solution with the interaction module Physikalisches Signal & Analytisches Signal .

Questions

$\text{Re}[s_+(t=0)]\ = \$

$\text{V}$

$\text{Im}[s_+(t=0)]\ = \$

$\text{V}$

	$s_+(t)$ results from $s(t)$ , if $\cos(\text{...})$ is replaced ${\rm e}^{{\rm j}(\text{...})}$ .
	If $s(t)$ is an even time function, $s_+(t)$ is purely real.
	At no time does the imaginary part of $s_+(t)$ disappear.

$\text{Re}[s_+(t=5 \ {\rm µ} \text{s})]\ = \$

$\text{V}$

$\text{Im}[s_+(t=5 \ {\rm µ} \text{s})]\ = \$

$\text{V}$

$\text{Re}[s_+(t=20 \ {\rm µ} \text{s})]\ = \$

$\text{V}$

$\text{Im}[s_+(t=20 \ {\rm µ} \text{s})]\ = \$

$\text{V}$

$|s_+(t)|_{\text{min}}\ = \$

$\text{V}$

$t_{\text{min}}\ = \$

${\rm µ} \text{s}$

Solutions

Solution

(1) By inverse Fourier transformation of

$S_+(f)$ considering the Verschiebungssatzes holds:

$s_{+}(t) = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 50}\hspace{0.05cm} t } + {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 60} \hspace{0.05cm} t }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 40}\hspace{0.05cm} t }.$

The expression describes the sum of three pointers rotating at different angular velocities.

In the above equation, for example, $\omega_{60} = 2\pi (f_{\rm T} + f_{\rm N}) = 2\pi \cdot 60 \ \text{kHz}$ .
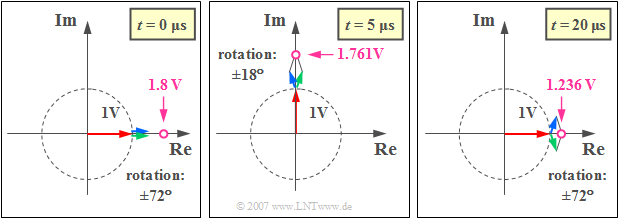
At time $t = 0$ all three pointers point in the direction of the real axis (see left graph).

One obtains the purely real value $s_+(t = 0) \;\underline{= 1.8 \ \text{V}}$ .

Drei verschiedene analytische Signale

(2) The first statement is correct and results from the Hilbert transform. On the other hand, the next two statements are not correct:

$s_+(t)$ is always a complex time function with the exception of the limiting case $s(t) = 0$ .
However, every complex function also has purely real values at some points in time.
The pointer composite always rotates in a mathematically positive direction.
If the sum vector crosses the real axis, the imaginary part disappears at this point and $s_+(t)$ is purely real.

(3) The period of the carrier signal is $T_0 = 1/f_T = 20 \ {\rm µ} \text{s}$ .

After $t = 5 \ {\rm µ} \text{s}$ (see middle graph) the carrier has thus rotated by $90^{\circ}$ gedreht.
The blue pointer (USB) rotates $20\%$ faster, the green one (LSB) $20\%$ slower than the red rotary pointer (carrier signal):

$s_{+}({\rm 5 \hspace{0.05cm} {\rm µ} s}) = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}50 \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 } + {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}60 \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}40 \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 } = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 90^\circ }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 108^\circ }+{\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 72^\circ }.$

Thus, the angles travelled in $5 \ {\rm µ} \text{s}$ by USB and LSB are $108^{\circ}$ and $72^{\circ}$ respectively.
Since at this time the real parts of USB and LSB compensate, $s_+(t=5 \ {\rm µ} \text{s})$ is purely imaginary and we obtain:

${\rm Im}\left[s_{+}(t = {\rm 5 \hspace{0.05cm} {\rm µ} s})\right] = {\rm 1 \hspace{0.05cm} V} + 2 \cdot {\rm 0.4 \hspace{0.05cm} V}\cdot \cos (18^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.761 \hspace{0.05cm} V}}.$

(4) After one revolution of the red carrier, i.e. at time $t$ = $T_0 = 20 \ {\rm µ} \text{s}$ , the blue pointer has already covered $72^{\circ}$ more and the green pointer correspondingly $72^{\circ}$ less. The sum of the three pointers is again purely real and results in accordance with the graph on the right:

${\rm Re}\left[s_{+}({\rm 20 \hspace{0.05cm} {\rm µ} s})\right] = {\rm 1 \hspace{0.05cm} V} + 2 \cdot {\rm 0.4 \hspace{0.05cm} V}\cdot \cos (72^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.236 \hspace{0.05cm} V}}.$

(5) The magnitude is minimum when the pointers of the two sidebands are offset from the carrier by $180^{\circ}$ . It follows:

$|s_{+}(t)|_{\rm min} = {\rm 1 \hspace{0.05cm} V} - 2 \cdot {\rm 0.4 \hspace{0.05cm} V} \hspace{0.15 cm}\underline{= {\rm 0.2 \hspace{0.05cm} V}}.$

Within one period $T_0$ of the carrier, a phase offset of $\pm72^{\circ}$ occurs with respect to the pointers of the two sidebands. From this follows:

$t_{\text{min}} = 180^{\circ}/72^{\circ} \cdot T_0 = 2.5 \cdot T_0 \;\underline{= 50 \ {\rm µ} \text{s}}.$