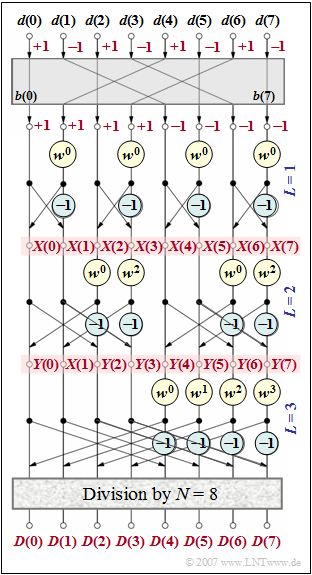
Exercise 5.5: Fast Fourier Transform

FFT algorithm for $N=8$

The graph shows the signal flow diagram of the FFT for $N = 8$. The associated spectral coefficients $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ are determined from the time coefficients $d(0), \hspace{0.03cm}\text{...} \hspace{0.1cm}, d(7)$ . The following applies to these with $0 ≤ μ ≤ 7$:

$$D(\mu) = \frac{1}{N}\cdot \sum_{\nu = 0 }^{N-1} d(\nu) \cdot {w}^{\hspace{0.03cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu}\hspace{0.05cm},$$

where the complex rotation factor $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}2\pi /N}$ is to be used, i.e. $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}\pi /4}$ für $N = 8$.

The alternating $±1$ sequence $\langle\hspace{0.05cm} d(ν)\hspace{0.05cm}\rangle$ is applied to the input.
After the bit reversal operation, this results in the sequence $\langle \hspace{0.05cm}b(\kappa)\hspace{0.05cm}\rangle$.

It holds that $b(κ) = d(ν)$, if $ν$ is represented as a dual number and the resulting three bits are written as $κ$ in reverse order. For example

$ν = 1$ $($binary $001)$ is followed by $κ = 4$ $($binary $100)$,
$d(2)$ remains at the same position $2$ $($binary $010)$.

The actual FFT algorithm happens for the example $N = 8$ in $\log_2 N = 3$ stages, denoted $L = 1$, $L =2$ and $L = 3$ . Further:

In each stage, four basic operations - so-called butterflies - are to be performed.
The values at the output of the first stage are designated in this task as $X(0),\hspace{0.03cm}\text{...} \hspace{0.1cm} , X(7)$ , those of the second as $Y(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , Y(7)$.
After the third and last stage, all values must be divided by $N$ . The final result $D(0), \hspace{0.03cm}\text{...} \hspace{0.1cm} , D(7)$ is then available here.

Hint:

This task belongs to the chapter Fast Fourier Transform (FFT).

Questions

$D(3) \ = \ $

$D(4) \ = \ $

	All $X$–values with even indices are equal to $2$.
	All $X$–values with odd indices are equal to $0$.

$Y(0) \ = \ $

$Y(4) \ = \ $

$D(\mu = 4) \ = \ $

$D(\mu \neq 4) \ = \ $

$D(\mu = 3) \ = \ $

$D(\mu = 4) \ = \ $

Solution

(1) According to the general DFT equation given on the specification sheet, with $w = \text{e}^{-\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}\pi /4}$ taking into account the alternating time coefficients:

$$8 \cdot D(3) = w^0 - w^3 + w^6- w^9+ w^{12}- w^{15}+ w^{18}- w^{21} = w^0 - w^3 + w^2- w^1+ w^{4}- w^{7}+ w^{6}- w^{5}\hspace{0.05cm}.$$

Here it is taken into account that due to the periodicity $w_9 = w_1$, $w_{12} = w_4$, $w_{15} = w_7$, $w_{18} = w_2$ und $w_{21} = w_5$ ist.
After re-sorting, the same applies:

$$8 \cdot D(3) = (w^0 + w^4) - (w^1 + w^5)+ (w^2 + w^6) - (w^3 + w^7) = (1 + w + w^2+ w^3) \cdot (w^0 + w^4)\hspace{0.05cm}.$$

Thus, because $w_0 = 1$ and $w_4 = \text{e}^{-\text{j}\pi } = \hspace{0.08cm} - \hspace{-0.08cm}1$ , we obtain $\underline {D(3) = 0}$.

(2) In analogy to sub-taske (1) , we now get:

$$ 8 \cdot D(4) = w^0 - w^4 + w^8- w^{12}+ w^{16}- w^{20}+ w^{24}- w^{28}= 4 \cdot (w^0 - w^4)= 8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\hspace{0.15 cm}\underline{D(4) = 1}\hspace{0.05cm}.$$

Example for the FFT algorithm

(3) Proposed solution 2 is correct:

The term $w^0 = 1$ does not have to be taken into account.
All output values with odd indices are zero by subtracting two identical input values.
The first statement is not true: Es gilt $X(0) = X(2) = +2$ and $X(4) = X(6) = - 2$.

(4) The multiplication with $w^{2} = -{\rm j}$ can be dispensed with, since in the signal flow diagram the corresponding input values are zero.

One thus obtains $Y(0) \;\underline{= 4}$ and $Y(4) \;\underline{= - \hspace{-0.03cm}4}$.
All other values are zero.

(5) Because of $Y(5) = Y(6) =Y(7) = 0$ , the multiplications with $w$, $w^2$ and $w^3$ do not matter in the third stage either. All spectral coefficients $D(\mu)$ therefore result in zero with the exception of

$$\hspace{0.15 cm}\underline{D(4)} = {1}/{N}\cdot \left[Y(0) - Y(4) \right ] \hspace{0.15 cm}\underline{= 1} \hspace{0.05cm}.$$

This result agrees with the results from (1) und (2) .

(6) Since both the time coefficients $d(ν)$ and all spectral coefficients $D(\mu)$ are purely real, there is no difference between the FFT and the IFFT.

This means at the same time: The input and output values can be interchanged.

Subtask (5) gave the following result:

$$d({\rm even}\hspace{0.15cm}\nu) = +1, \hspace{0.2cm}d({\rm odd}\hspace{0.15cm}\nu)= -1$$

$$\Rightarrow \hspace{0.3cm}D(\mu = 4)= 1,\hspace{0.2cm}D(\mu \ne 4)= 0.$$

By swapping the input and output values, we arrive at problem (6):

$$d(\nu = 4)= 1, \hspace{0.2cm}d(\nu \ne 4)= 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}D({\rm gerades}\hspace{0.15cm}\mu) = +1, \hspace{0.2cm}D({\rm ungerades}\hspace{0.15cm}\mu)= -1 \hspace{0.05cm}.$$

In particular, this results in $D(3) \; \underline{= -1}$ und $D(4) \; \underline{= +1}$.