Exercise 4.3: Iterative Decoding at the BSC

BSC–Modell und mögliche Empfangswerte

Wir betrachten in dieser Aufgabe zwei Codes:

den Single Parity–Code ⇒ $\text{SPC (3, 2, 2)}$:

$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (0, 1, 1), \hspace{0.1cm} (1, 0, 1), \hspace{0.1cm} (1, 1, 0) \hspace{0.05cm} \big ) \hspace{0.05cm}, $$

den Wiederholungscode ⇒ $\text{RC (3, 1, 3)}$:

$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (1, 1, 1) \hspace{0.05cm} \big ) \hspace{0.05cm}.$$

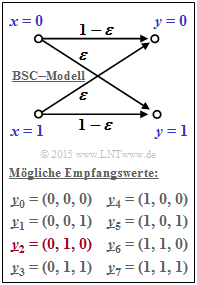
Der Kanal wird auf Bitebene durch das BSC–Modell beschrieben. Entsprechend der Grafik gilt dabei:

$${\rm Pr}(y_i \ne x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}\varepsilon = 0.269\hspace{0.05cm},$$

$${\rm Pr}(y_i = x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1-\varepsilon = 0.731\hspace{0.05cm}.$$

Hierbei bezeichnet $\varepsilon$ die Verfälschungswahrscheinlichkeit des BSC–Modells.

Bis auf die letzte Teilaufgabe wird stets von folgendem Empfangswert ausgegangen:

$$\underline{y} = (0, 1, 0) =\underline{y}_2 \hspace{0.05cm}. $$

Die hier gewählte Indizierung aller möglichen Empfangsvektoren kann der Grafik entnommen werden.

Der meistens betrachtete Vektor $\underline{y}_2$ ist hierbei rot hervorgehoben.
Für die Teilaufgabe (6) gilt dann:

$$\underline{y} = (1, 1, 0) =\underline{y}_6 \hspace{0.05cm}. $$

Zur Decodierung sollen in der Aufgabe untersucht werden:

die Syndromdecodierung, die bei den betrachteten Codes dem Konzept Hard Decision Maximum Likelihood Detection (HD–ML) folgt
(Softwerte liegen beim BSC nicht vor),
die symbolweise Soft–in Soft–out Decodierung (SISO) entsprechend dieses Abschnitts.

Hinweise:

Die Aufgabe bezieht sich auf das Kapitel Soft–in Soft–out Decoder.
Bezug genommen wird insbesondere auf die Seiten

Symbolweise Soft–in Soft–out_Decodierung, sowie

Binary Symmetric Channel.

Das vom Decoder ausgewählte Codewort wird in den Fragen mit $\underline{z}$ bezeichnet.

Fragebogen

Musterlösung

Solution

(1) Richtig ist der Lösungsvorschlag 3:

Das Empfangswort $\underline{y}_2 = (0, 1, 0)$ ist kein gültiges Codewort des Single Parity–check Codes SPC (3, 2). Somit ist die erste Aussage falsch.
Da der SPC (3, 2) zudem nur die minimale Distanz $d_{\rm min} = 2$ aufweist, kann auch kein Fehler korrigiert werden.

(2) Richtig ist der Lösungsvorschlag 2:

Die möglichen Codeworte beim RP (3, 1) sind $\underline{x}_0 = (0, 0, 0)$ und $\underline{x}_1 = (1, 1, 1)$.
Die minimale Distanz dieses Codes beträgt $d_{\rm min} = 3$, so dass $t = (d_{\rm min} \, - 1)/2 = 1$ Fehler korrigiert werden kann.
Neben $\underline{y}_0 = (0, 0, 0)$ werden auch $\underline{y}_1 = (0, 0, 1), \ \underline{y}_2 = (0, 1, 0)$ und $\underline{y}_4 = (1, 0, 0)$ dem Decodierergebnis $\underline{x}_0 = (0, 0, 0)$ zugeordnet.

(3) Entsprechend dem BSC–Modell gilt für die bedingte Wahrscheinlichkeit, dass $\underline{y}_2 = (0, 1, 0)$ empfangen wird, unter der Voraussetzung, dass $\underline{x}_0 = (0, 0, 0)$ gesendet wurde:

$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) = (1-\varepsilon)^2 \cdot \varepsilon\hspace{0.05cm}.$$

Der erste Term $(1 \, –\varepsilon)^2$ gibt dabei die Wahrscheinlichkeit dafür an, dass das erste und das dritte Bit richtig übertragen wurden und $\varepsilon$ berücksichtigt die Verfälschungswahrscheinlichkeit für das zweite Bit.

Entsprechend gilt für das zweite mögliche Codewort $\underline{x}_1 = (1, 1, 1)$:

$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) = \varepsilon^2 \cdot (1-\varepsilon) \hspace{0.05cm}.$$

Nach dem Satz von Bayes gilt dann für die Rückschlusswahrscheinlichkeiten:

$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_0)} {{\rm Pr}(\underline{y} = \underline{y}_2)} \hspace{0.05cm},$$

$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_1 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_1)} {{\rm Pr}(\underline{y} = \underline{y}_2)} $$

$$\Rightarrow \hspace{0.3cm} S = \frac{{\rm Pr(richtige \hspace{0.15cm}Entscheidung)}} {{\rm Pr(falsche \hspace{0.15cm}Entscheidung) }} = \frac{(1-\varepsilon)^2 \cdot \varepsilon}{\varepsilon^2 \cdot (1-\varepsilon)}= \frac{(1-\varepsilon)}{\varepsilon}\hspace{0.05cm}.$$

Mit $\varepsilon = 0.269$ erhält man folgende Zahlenwerte:

$$S = {0.731}/{0.269}\hspace{0.15cm}\underline {= 2.717}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm ln}\hspace{0.15cm}(S)\hspace{0.15cm} \underline {= 1}\hspace{0.05cm}.$$

(4) Das Vorzeichen des Kanal–$L$–Wertes $L_{\rm K}(i)$ ist positiv, falls $y_i = 0$, und negativ für $y_i = 1$.

Der Betrag gibt die Zuverlässigkeit von $y_i$ an. Beim BSC–Modell gilt $|L_{\rm K}(i)| = \ln {(1 \, – \varepsilon)/\varepsilon} = 1$ für alle $i$. Also:

Iterative Decodierung von $(+1, –1, +1)$

$$\underline {L_{\rm K}}(1)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm},\hspace{0.5cm} \underline {L_{\rm K}}(2)\hspace{0.15cm} \underline {= -1}\hspace{0.05cm},\hspace{0.5cm} \underline {L_{\rm K}}(3)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm}.$$

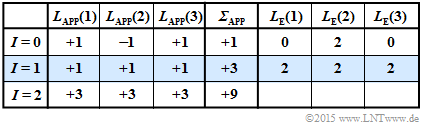
(5) Die nebenstehende Tabelle verdeutlicht die iterative symbolweise Decodierung ausgehend von $\underline{y}_2 = (0, \, 1, \, 0)$.
Diese Ergebnisse lassen sich wie folgt interpretieren:

Die Vorbelegung (Iteration $I = 0$) geschieht entsprechend $\underline{L}_{\rm APP} = \underline{L}_{\rm K}$. Eine harte Entscheidung ⇒ „$\sign {\underline{L}_{\rm APP}(i)}$" würde zum Decodierergebnis $(0, \, 1, \, 0)$ führen. Die Zuverlässigkeit dieses offensichtlich falschen Ergebnisses wird mit $|{\it \Sigma}| = 1$ angegeben. Dieser Wert stimmt mit dem in Teilaufgaben (3) berechneten „$\ln (S)$" überein.
Nach der ersten Iteration $(I = 1)$ sind alle Aposteriori–$L$–Werte $L_{\rm APP}(i) = +1$. Eine harte Entscheidung würde hier das (voraussichtlich) richtige Ergebnis $\underline{x}_{\rm APP} = (0, \, 0, \, 0)$ liefern. Die Wahrscheinlichkeit, dass dieses Ergebnis richtig ist, wird durch $|{\it \Sigma}_{\rm APP}| = 3$ quantifiziert:

$${\rm ln}\hspace{0.25cm}\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = 3 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^3 \approx 20$$

$$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {20}/{21} {\approx 95.39\%}\hspace{0.05cm}.$$

Die zweite Iteration bestätigt das Decodierergebnis der ersten Iteration. Die Zuverlässigkeit wird hier sogar mit „$9$" beziffert. Dieser Wert kann wie folgt interpretiert werden:

$$\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^9 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {{\rm e}^9}/{({\rm e}^9+1)} \approx 99.99\% \hspace{0.05cm}.$$

Mit jeder weiteren Iteration nimmt der Zuverlässigkeitswert und damit die Wahrscheinlichkeit ${\rm Pr}(\underline{x}_0 | \underline{y}_2)$ drastisch zu ⇒ Alle Lösungsvorschläge sind richtig.

Iterative Decodierung von $(–1, –1, +1)$

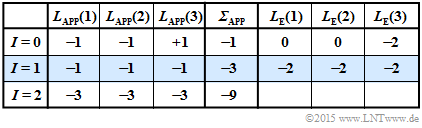
(6) Richtig sind die Lösungsvorschläge 2 und 3:

Für den Empfangsvektor $\underline{y}_6 = (1, \, 1, \, 0)$ gilt die zweite Tabelle.

Der Decoder entscheidet sich nun für die Folge $\underline{x}_1 = (1, \, 1, \, 1)$.
Der Fall „$\underline{y}_3 = (1, \, 1, \, 0)$ empfangen unter der Voraussetzung $\underline{x}_1 = (1, \, 1, \, 1)$ gesendet" würde genau der in der letzten Teilaufgabe betrachteten Konstellation „$\underline{y}_2 = (1, \, 0, \, 1)$ empfangen und $\underline{x}_0 = (0, \, 0, \, 0)$ gesendet" entsprechen.
Da aber $\underline{x}_0 = (0, \, 0, \, 0)$ gesendet wurde, gibt es nun zwei Bitfehler mit folgender Konsequenz:

Der iterative Decoder entscheidet falsch.
Mit jeder weiteren Iteration wird die falsche Entscheidung als zuverlässiger deklariert.

	Die HD–Syndromdecodierung liefert das Ergebnis $\underline{z} = (0, \, 1, \, 0)$.
	Die HD–Syndromdecodierung liefert das Ergebnis $\underline{z} = (0, \, 0, \, 0)$.
	Die HD–Syndromdecodierung versagt hier.

	Ab der ersten Iteration sind alle Vorzeichen von $L_{\rm APP}(i)$ positiv.
	Bereits nach der zweiten Iteration ist ${\rm Pr}(\underline{x}_0\hspace{0.05cm} \|\hspace{0.05cm} \underline{y}_2)$ größer als $99\%$.
	Mit jeder Iteration werden die Beträge $L_{\rm APP}(i)$ größer.

	Der iterative Decoder entscheidet richtig.
	Der iterative Decoder entscheidet falsch.
	Die „Zuverlässigkeit" für „$\underline{y}_6 \Rightarrow \underline{x}_0$" steigt mit wachsendem $I$.