Contents
The Huffman algorithm
We now assume that the source symbols $q_\nu$ originate from an alphabet $\{q_μ\} = \{$ $\rm A$, $\rm B$ , $\rm C$ , ...$\}$ with the symbol range $M$ and are statistically independent of each other. For example, for the symbol range $M = 8$:
- $$\{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm B}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm C}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm D}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm E}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm F}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm G}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm H}\hspace{0.05cm} \}\hspace{0.05cm}.$$
In 1952 - i.e. shortly after Shannon's groundbreaking publications David A. Huffman gave an algorithm for the construction of optimal prefix-free codes.
This Huffman Algorithm is to be given here without derivation and proof, whereby we restrict ourselves to binary codes. That is: for the code symbols, let $c_ν ∈ \{$0, 1$\}$ always hold.
Here is the „recipe”:
- Order the symbols according to decreasing probabilities of occurrence.
- Combine the two most improbable symbols into a new symbol.
- Repeat (1) and (2), until only two (combined) symbols remain.
- Code the more probable set of symbols with 1 and the other set with 0.
- In the opposite direction (i.e. from bottom to top) , add 1 or 0 to the respective binary codes of the split subsets according to the probabilities.
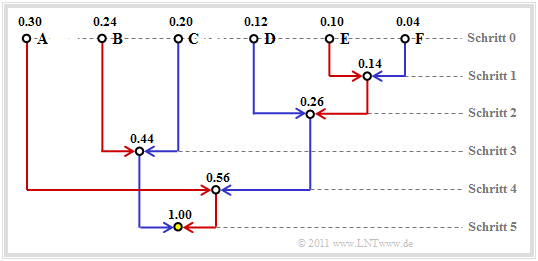
$\text{Example 1:}$ Without limiting the generality, we assume that the $M = 6$ symbols $\rm A$, ... , $\rm F$ are already ordered according to their probabilities:
- $$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm}.$$
By pairwise combination and subsequent sorting, the following symbol combinations are obtained in five steps
(resulting probabilities in brackets):
- 1. $\rm A$ (0.30), $\rm B$ (0.24), $\rm C$ (0.20), $\rm EF$ (0.14), $\rm D$ (0.12),
- 2. $\rm A$ (0.30), $\rm EFD$ (0.26), $\rm B$ (0.24), $\rm C$ (0.20),
- 3. $\rm BC$ (0.44), $\rm A$ (0.30), $\rm EFD$ (0.26),
- 4. $\rm AEFD$ (0.56), $\rm BC$ (0.44),
- 5. Root $\rm AEFDBC$ (1.00).
Backwards – i.e. according to steps (5) to (1) – the assignment to binary symbols then takes place.
An x indicates that bits still have to be added in the next steps:
- 5. $\rm AEFD$ → 1x, $\rm BC$ → 0x,
- 4. $\underline{\rm A}$ → 11, $\rm EFD$ → 10x,
- 3. $\underline{\rm B}$ → 01, $\underline{\rm C}$ → 00,
- 2. $\rm EF$ → 101x, $\underline{\rm D}$ → 100,
- 1. $\underline{\rm E}$ → 1011, $\underline{\rm F}$ → 1010.
The underlines mark the final binary coding..
On the term „entropy coding”
We continue to assume the probabilities and assignments of the last example:
- $$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm};$$
- $$\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 11} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 01} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 00} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 100} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1011} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1010} \hspace{0.05cm}.$$
Thus, of the six source symbols, three are coded with two bits each, one with three bits and two symbols $(\rm E$ and $\rm F)$ with four bits each.
The average codeword length thus results in
- $$L_{\rm M} = (0.30 \hspace{-0.05cm}+ \hspace{-0.05cm}0.24 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.20) \cdot 2 + 0.12 \cdot 3 + (0.10 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.04 ) \cdot 4 = 2.4 \,{\rm bit/source symbol} \hspace{0.05cm}.$$
From the comparison with the source entropy $H = 2.365 \ \rm bit/source symbol$ bit/source symbol one can see the efficiency of the Huffman coding.
$\text{Merke:}$ Note: There is no prefix-free $($⇒ immediately decodable$)$ code that leads to a smaller mean codeword length $L_{\rm M}$ than the Huffman code by exploiting the occurrence probabilities alone. . In this sense, the Huffman code is optimal..
$\text{Example 2:}$ If the symbol probabilities were
- $$p_{\rm A} = p_{\rm B} = p_{\rm C} = 1/4 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 1/8 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = p_{\rm F} = 1/16 \hspace{0.05cm},$$
then the same would apply to the entropy and to the mean codeword length:
- $$H = 3 \cdot 1/4 \cdot {\rm log_2}\hspace{0.1cm}(4) + 1/8 \cdot {\rm log_2}\hspace{0.1cm}(8) + 2 \cdot 1/16 \cdot {\rm log_2}\hspace{0.1cm}(16) = 2.375 \,{\rm bit/source symbol}\hspace{0.05cm},$$
- $$L_{\rm M} = 3 \cdot 1/4 \cdot 2 + 1/8 \cdot 3 + 2 \cdot 1/16 \cdot 4 = 2.375 \,{\rm bit/source symbol} \hspace{0.05cm}.$$
This property $L_{\rm M} = H +\varepsilon$ with $\varepsilon \to 0$ at suitable occurrence probabilities explains the term entropy coding:
In this form of source coding, one tries to adapt the length $L_μ$ of the binary sequence (consisting of zeros and ones) for the symbol $q_μ$ according to the entropy calculation to its occurrence probability $p_μ$ as follows:
- $$L_{\mu} = {\rm log}_2\hspace{0.1cm}(1/p_{\mu} ) \hspace{0.05cm}.$$
Of course, this does not always succeed, but only if all occurrence probabilities $p_μ$ can be represented in the form $2^{–k}$ with $k = 1, \ 2, \ 3,$ ...
- In this special case - and only in this case - the mean codeword length $L_{\rm M}$ coincides exactly with the source entropy $H$ $(\varepsilon = 0$, see $\text{example 2})$.
- According to the source encoding theorem there is no (decodable) code that gets by with fewer binary characters per source symbol on average.
Darstellung des Huffman–Codes als Baumdiagramm
Häufig wird zur Konstruktion des Huffman–Codes eine Baumstruktur verwendet. Für das bisher betrachtete Beispiel ist diese in der folgenden Grafik dargestellt:
Man erkennt:
- Bei jedem Schritt des Huffman–Algorithmus werden die beiden Zweige mit den jeweils kleinsten Wahrscheinlichkeiten zusammengefasst.
- Der Knoten im ersten Schritt fasst die zwei Symbole $\rm E$ und $\rm F$ mit den aktuell kleinsten Wahrscheinlichkeiten zusammen. Dieser neue Knoten ist mit $p_{\rm E} + p_{\rm F} = 0.14$ beschriftet.
- Der vom Symbol mit der kleineren Wahrscheinlichkeit $($hier $\rm F)$ zum Summenknoten verlaufende Zweig ist blau eingezeichnet, der andere Zweig $($für $\rm E)$ rot.
Nach fünf Schritten ist man bei der Baumwurzel („Root”) mit der Gesamtwahrscheinlichkeit $1.00$ angelangt. Verfolgt man nun den Verlauf von der Wurzel (in obiger Grafik mit gelber Füllung) zu den einzelnen Symbolen zurück, so kann man aus den Farben der einzelnen Zweige die Symbolzuordnung ablesen.
Mit den Zuordnungen „rot” → 1 und „blau” → 0 ergibt sich beispielsweise von der Wurzel zu Symbol
- $\rm A$: rot, rot → 11,
- $\rm B$: blau, rot → 01,
- $\rm C$: blau, blau → 00,
- $\rm D$: rot, blau, blau → 100,
- $\rm E$: rot, blau, rot, rot → 1011,
- $\rm F$: rot, blau, rot, blau → 1010.
Die (einheitliche) Zuordnung „rot” → 0 und „blau” → 1 würde ebenfalls zu einem optimalen präfixfreien Huffman–Code führen.
$\text{Beispiel 3:}$ Die folgende Grafik zeigt die Huffman–Codierung von $49$ Symbolen $q_ν ∈ \{$ $\rm A$, $\rm B$, $\rm C$, $\rm D$, $\rm E$, $\rm F$ $\}$ mit der auf der letzten Seite hergeleiteten Zuordnung.
- Die binäre Codesymbolfolge weist die mittlere Codewortlänge $L_{\rm M} = 125/49 = 2.551$ auf.
- Die verschiedenen Farben dienen ausschließlich zur besseren Orientierung.
Aufgrund der kurzen Quellensymbolfolge $(N = 49)$ weichen die Auftrittshäufigkeiten $h_{\rm A}$, ... , $h_{\rm F}$ der simulierten Folgen (manchmal) signifikant von den gegebenen Wahrscheinlichkeiten $p_{\rm A}$, ... , $p_{\rm F}$ ab:
- $$p_{\rm A} = 0.30 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm A} = 16/49 \approx 0.326 \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = 0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm B} = 7/49 \approx 0.143 \hspace{0.05cm},$$
- $$p_{\rm C} =0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm C}= 9/49 \approx 0.184 \hspace{0.05cm},\hspace{0.6cm}p_{\rm D} = 0.12 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm D} = 7/49 \approx 0.143 \hspace{0.05cm},$$
- $$p_{\rm E}=0.10 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 \hspace{0.05cm},\hspace{0.6cm}p_{\rm F} = 0.04 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 \hspace{0.05cm}.$$
Damit ergibt sich ein etwas größerer Entropiewert:
- $$H ({\rm bez\ddot{u}glich }\hspace{0.15cm}p_{\mu}) = 2.365 \ {\rm bit/Quellensymbol}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H ({\rm bez\ddot{u}glich }\hspace{0.15cm}h_{\mu}) = 2.451 \ {\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Würde man den Huffman–Code mit diesen „neuen” Wahrscheinlichkeiten $h_{\rm A}$, ... , $h_{\rm F}$ bilden, so ergäben sich folgende Zuordnungen:
- $\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$11$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$100$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$00$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$101$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$010$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$011$\hspace{0.05cm}.$
Nun würden nur $\rm A$ und $\rm C$ mit zwei Bit dargestellt, die anderen vier Symbole durch jeweils drei Bit.
- Die Codesymbolfolge hätte dann eine Länge von $(16 + 9) · 2 + (7 + 7 + 5 + 5) · 3 = 122$ Bit, wäre also um drei Bit kürzer als nach der bisherigen Codierung.
- Die mittlere Codewortlänge wäre dann $L_{\rm M} = 122/49 ≈ 2.49$ bit/Quellensymbol anstelle von $L_{\rm M}≈ 2.55$ bit/Quellensymbol.
$\text{Fazit:}$ Dieses Beispiel lässt sich wie folgt interpretieren:
- Die Huffman–Codierung lebt von der (genauen) Kenntnis der Symbolwahrscheinlichkeiten. Sind diese sowohl dem Sender als auch dem Empfänger bekannt, so ist die mittlere Codewortlänge $L_{\rm M}$ oft nur unwesentlich größer als die Quellenentropie $H$.
- Insbesondere bei kleinen Dateien kann es zu Abweichungen zwischen den (erwarteten) Symbolwahrscheinlichkeiten $p_μ$ und den (tatsächlichen) Häufigkeiten $h_μ$ kommen. Besser wäre es hier, für jede Datei einen eigenen Huffman–Code zu generieren, der auf den tatsächlichen Gegebenheiten $(h_μ)$ basiert.
- In diesem Fall muss aber dem Decoder auch der spezifische Huffman–Code mitgeteilt werden. Dies führt zu einem gewissen Overhead, der nur wieder bei längeren Dateien vernachlässigt werden kann. Bei kleinen Dateien lohnt sich dieser Aufwand nicht.
Einfluss von Übertragungsfehlern auf die Decodierung
Der Huffman–Code ist aufgrund der Eigenschaft „präfixfrei” verlustlos.
- Das bedeutet: Aus der binären Codesymbolfolge lässt sich die Quellensymbolfolge vollständig rekonstruieren.
- Kommt es aber bei der Übertragung zu einem Fehler $($aus einer 0 wird eine 1 bzw. aus einer 1 eine 0$)$, so stimmt natürlich auch die Sinkensymbolfolge $〈v_ν〉$ nicht mit der Quellensymbolfolge $〈q_ν〉$ überein.
Die beiden folgenden Beispiele zeigen, dass ein einziger Übertragungsfehler manchmal eine Vielzahl von Fehlern hinsichtlich des Ursprungstextes zur Folge haben kann.
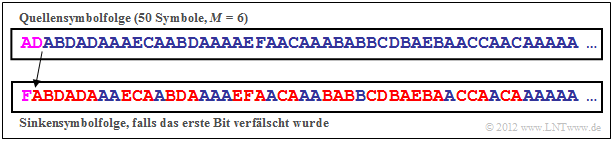
$\text{Beispiel 4:}$ Wir betrachten die gleiche Quellensymbolfolge und den gleichen Huffman–Code wie auf der vorherigen Seite.
- Die obere Grafik zeigt, dass bei fehlerfreier Übertragung aus der codierten Binärfolge 111011... wieder die ursprüngliche Quellenfolge $\rm AEBFCC$... rekonstruiert werden kann.
- Wird aber zum Beispiel das Bit 6 verfälscht $($von 1 auf 0, rote Markierung in der mittlere Grafik$)$, so wird aus dem Quellensymbol $q_2 = \rm E$ das Sinkensymbol $v_2 =\rm F$.
- Eine Verfälschung von Bit 13 $($von 0 auf 1, rote Markierung in der unteren Grafik$)$ führt sogar zu einer Verfälschung von vier Quellensymbolen: $\rm CCEC$ → $\rm DBBD$.
$\text{Beispiel 5:}$ Eine zweite Nachrichtenquelle mit Symbolumfang $M = 6$ sei durch folgende Symbolwahrscheinlichkeiten gekennzeichnet:
- $$p_{\rm A} = 0.50 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.19 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.11 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.09 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.06 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.05 \hspace{0.05cm}.$$
Hier führt der Huffman–Algorithmus zu folgender Zuordnung:
- $\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$0$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$111$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$101$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$100$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$1101$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.15cm}$1100$\hspace{0.05cm}.$
Die Quellensymbolfolge $\rm ADABD$... (siehe Grafik) wird somit durch die Codesymbolfolge 0'100'0'111'100' ... dargestellt. Die Hochkommata dienen hierbei lediglich der Orientierung für den Leser.
Bei der Übertragung wird nun das erste Bit verfälscht: Anstelle von 01000111100... empfängt man somit 11000111100...
- Aus den beiden ersten Quellensymbolen $\rm AD$ → 0100 wird nach der Decodierung das Sinkensymbol $\rm F$ → 1100.
- Die weiteren Symbole werden dann wieder richtig detektiert, aber nun nicht mehr beginnend bei der Position $ν = 3$, sondern bei $ν = 2$.
Je nach Anwendung sind die Auswirkungen unterschiedlich:
- Handelt es sich bei der Quelle um einen natürlichen Text und bei der Sinke um einen Menschen, so bleibt der Großteil des Textes für den Leser verständlich.
- Ist die Sinke jedoch ein Automat, der sukzessive alle $v_ν$ mit den entsprechenden $q_ν$ vergleicht, so ergibt sich eine Verfälschungshäufigkeit von deutlich über $50\%$.
- Nur die blauen Symbole der Sinkensymbolfolge $〈v_ν〉$ stimmen dann (zufällig) mit den Quellensymbolen $q_ν$ überein, während rote Symbole auf Fehler hinweisen.
Anwendung der Huffman–Codierung auf $k$–Tupel
Der Huffman–Algorithmus in seiner Grundform liefert dann unbefriedigende Ergebnisse, wenn
- eine Binärquelle $(M = 2)$ vorliegt, zum Beispiel mit dem Symbolvorrat $\{$ $\rm X$, $\rm Y$ $\}$,
- es statistische Bindungen zwischen den Symbolen der Eingangsfolge gibt,
- die Wahrscheinlichkeit des häufigsten Symbols deutlich größer ist als $50\%$.
Abhilfe schafft man in diesen Anwendungsfällen,
- in dem man mehrere Symbole zusammenfasst, und
- den Huffman–Algorithmus auf einen neuen Symbolvorrat $\{$ $\rm A$, $\rm B$, $\rm C$, $\rm D$, ... $\}$ anwendet.
Bildet man $k$–Tupel, so steigt der Symbolumfang von $M$ auf $M\hspace{-0.01cm}′ = M^k$.
Wir wollen im folgenden Beispiel die Vorgehensweise anhand einer Binärquelle verdeutlichen. Weitere Beispiele finden Sie in
- der Aufgabe 2.7,
- der Aufgabe 2.7Z und
- der Aufgabe 2.8.
$\text{Beispiel 6:}$ Gegeben sei eine gedächtnislose Binärquelle $(M = 2)$ mit den Symbolen $\{$ $\rm X$, $\rm Y$ $\}$:
- Die Symbolwahrscheinlichkeiten seien $p_{\rm X} = 0.8$ und $p_{\rm Y} = 0.2$.
- Damit ergibt sich die Quellenentropie zu $H = 0.722$ bit/Quellensymbol.
- Wir betrachten die Symbolfolge $\{\rm XXXYXXXXXXXXYYXXXXXYYXXYXYXXYX\ \text{...} \}$ mit nur wenigen $\rm Y$–Symbolen an den Positionen 4, 13, 14, ...
Der Huffman–Algorithmus kann auf diese Quelle direkt nicht angewendet werden, das heißt, man benötigt ohne weitere Maßnahme für jedes binäre Quellensymbol auch ein Bit. Aber:
- Fasst man jeweils zwei binäre Symbole zu einem Zweiertupel $(k = 2)$ entsprechend $\rm XX$ → $\rm A$, $\rm XY$ → $\rm B$, $\rm YX$ → $\rm C$, $\rm YY$ → $\rm D$ zusammen, so kann man „Huffman” auf die resultierende Folge → $\rm ABAACADAABCBBAC$ ... → mit $M\hspace{-0.01cm}′ = 4$ → anwenden. Wegen
- $$p_{\rm A}= 0.8^2 = 0.64 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= 0.8 \cdot 0.2 = 0.16 = p_{\rm C} \hspace{0.05cm}, \hspace{0.2cm} p_{\rm D}= 0.2^2 = 0.04$$
- erhält man $\rm A$ → 1, $\rm B$ → 00, $\rm C$ → 011, $\rm D$ → 010 sowie
- $$L_{\rm M}\hspace{0.03cm}' = 0.64 \cdot 1 + 0.16 \cdot 2 + 0.16 \cdot 3 + 0.04 \cdot 3 =1.56\,{\rm bit/Zweiertupel} $$
- $$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.03cm}'}/{2} = 0.78\ {\rm bit/Quellensymbol}\hspace{0.05cm}.$$
- Nun bilden wir Dreiertupel $(k = 3)$ → entsprechend
- $\rm XXX$ → $\rm A$, $\rm XXY$ → $\rm B$, $\rm XYX$ → $\rm C$, $\rm XYY$ → $\rm D$, $\rm YXX$ → $\rm E$, $\rm YXY$ → $\rm F$, $\rm YYX$ → $\rm G$, $\rm YYY$ → $\rm H$.
- Für die oben angegebene Eingangsfolge kommt man zur äquivalenten Folge $\rm AEBAGADBCC$ ... (basierend auf dem neuen Symbolumfang $M\hspace{-0.01cm}′ = 8$) und zu folgenden Wahrscheinlichkeiten:
- $$p_{\rm A}= 0.8^3 = 0.512 \hspace{0.05cm}, \hspace{0.5cm}p_{\rm B}= p_{\rm C}= p_{\rm E} = 0.8^2 \cdot 0.2 = 0.128\hspace{0.05cm},\hspace{0.5cm} p_{\rm D}= p_{\rm F}= p_{\rm G} = 0.8 \cdot 0.2^2 = 0.032 \hspace{0.05cm}, \hspace{0.5cm}p_{\rm H}= 0.2^3 = 0.008\hspace{0.05cm}.$$
- Die Huffman–Codierung lautet somit:
- $\rm A$ → 1, $\rm B$ → 011, $\rm C$ → 010, $\rm D$ → 00011, $\rm E$ → 001, $\rm F$ → 00010, $\rm G$ → 00001, $\rm H$ → 00000.
- Damit erhält man für die mittlere Codewortlänge:
- $$L_{\rm M}\hspace{0.03cm}' = 0.512 \cdot 1 + 3 \cdot 0.128 \cdot 3 + (3 \cdot 0.032 + 0.008) \cdot 5 =2.184 \,{\rm bit/Dreiertupel} $$
- $$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.03cm}'}/{3} = 0.728\ {\rm bit/Quellensymbol}\hspace{0.05cm}.$$
- In diesem Beispiel wird also bereits mit $k = 3$ die Quellenentropie $H = 0.722$ bit/Quellensymbol nahezu erreicht.
Aufgaben zum Kapitel
Aufgabe 2.6: Zur Huffman-Codierung
Aufgabe 2.6Z: Nochmals zum Huffman–Code
Aufgabe 2.7: Huffman-Anwendung für binäre Zweiertupel
Aufgabe 2.7Z: Huffman-Codierung für Zweiertupel einer Ternärquelle
Aufgabe 2.8: Huffman-Anwendung bei einer Markovquelle
Aufgabe 2.9: Huffman-Decodierung nach Fehlern