Exercise 2.1Z: Sum Signal
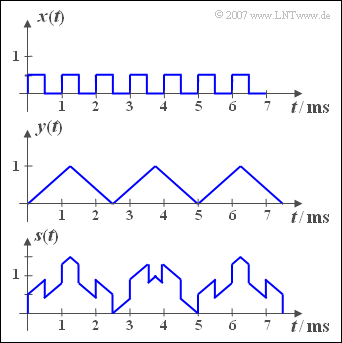
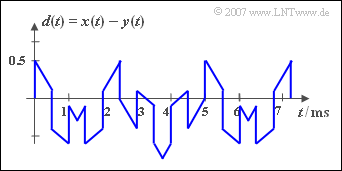
The adjacent diagram shows the periodic signals ${x(t)}$ and ${y(t)}$, from which the sum ${s(t)}$ – sketched in the lower diagram – and the difference ${d(t)}$ are formed.
Furthermore, in this task we consider the signal ${w(t)}$, which results from the sum of two periodic signals ${u(t)}$ and $v(t)$ . The base frequencies of these signals are
- $f_u = 998 \,\text{Hz},$
- $f_v = 1002 \,\text{Hz}.$
That is all we know about the signals ${u(t)}$ and $v(t)$.
Hints:
- The exercise belongs to the chapter General description of periodic signals.
- With the interactive applet Period Duration of Periodic Signals the resulting period duration of two harmonic oscillations can be determined.
Questions
Solution
(2) The following applies to the triangular signal: $T_y = 2.5 \,\text{ms}$ und $f_y \hspace{0.15cm}\underline{= 0.4\, \text{kHz}}$.
(3) The base frequency $f_s$ of the sum signal $s(t)$ is the greatest common divisor $f_x = 1 \,\text{kHz}$ and $f_y = 0.4 \,\text{kHz}$.
- Daraus folgt $f_s = 200 \,\text{Hz}$ und die Periodendauer $T_s\hspace{0.15cm}\underline{ = 5 \,\text{ms}}$, wie auch aus der grafischen Darstellung des Signals ${s(t)}$ auf der Angabenseite hervorgeht.
(4) The period duration $T_d$ does not change compared to the period duration $T_s$ , if the signal ${y(t)}$ is not added but subtracted: $T_d = T_s \hspace{0.15cm}\underline{= 5\, \text{ms}}$.
(5) The greatest common divisor of $f_u = 998 \,\text{Hz}$ and $f_{v} = 1002 \,\text{Hz}$ is $f_w = 2 \,\text{Hz}$.
- The inverse of this gives the period duration $T_w \hspace{0.15cm}\underline{= 500 \,\text{ms}}$.