Exercise 3.3: Entropy of Ternary Quantities

Given entropy functions

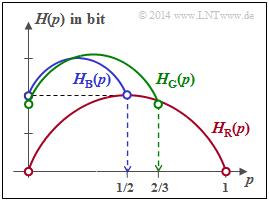
On the right you see the entropy functions $H_{\rm R}(p)$, $H_{\rm B}(p)$ and $H_{\rm G}(p)$, where $\rm R$ stands for "red", $\rm B$ for "blue" and $\rm G$ for "green". The probability functions are for all random variables:

$$P_X(X) = [\hspace{0.05cm}p_1\hspace{0.05cm},\ p_2\hspace{0.05cm},\ p_3\hspace{0.05cm}]\hspace{0.3cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} |X| = 3\hspace{0.05cm}.$$

For the questionnaire, the relationship $p_1 = p$ and $p_2 = 1 - p_3- p$.

The probability function of a random variable

$$X = \big \{\hspace{0.05cm}x_1\hspace{0.05cm}, \hspace{0.15cm} x_2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} x_{\mu}\hspace{0.05cm}, \hspace{0.05cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} x_{M}\hspace{0.05cm}\big \}$$

with the symbolic range $|X| = M$ is generally:

$$P_X(X) = [\hspace{0.05cm}p_1\hspace{0.05cm}, \hspace{0.15cm} p_2\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.1cm} ,\hspace{0.15cm} p_{\mu}\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm} , \hspace{0.15cm} p_{M}\hspace{0.05cm}]\hspace{0.05cm}.$$

The entropy (uncertainty) of this random variable is calculated according to the equation

$$H(X) = {\rm E} \big [\log_2 \hspace{0.05cm} {1}/{P_X(X)} \big ]\hspace{0.05cm},$$

and always lies in the range $0 \le H(X) \le \log_2 \hspace{0.05cm} |X|$.

The lower bound $H(X) = 0$ results when any probability $p_\mu = 1$ and all others are zero.

The upper bound is to be derived here as in the lecture "Information Theory" by Gerhard Kramer at the TU Munich:

Upper bound estimate for the natural logarithm

By extending the above equation by $|X|$ in the numerator and denominator, using $\log_2 \hspace{0.05cm}x= \ln(x)/\ln(2)$, we obtain:

$$H(X) = \frac{1}{{\rm ln}(2)}\cdot {\rm E} \left [{\rm ln} \hspace{0.1cm} \frac{1}{|X| \cdot P_X(X)} \right ] + {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$

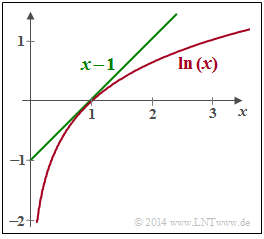
As can be seen from the graph opposite, the estimation $\ln(x) \le x-1$ holds with the identity for $x=1$. Thus, it can be written:

$$H(X) \le \frac{1}{{\rm ln}(2)}\cdot {\rm E} \left [\frac{1}{|X| \cdot P_X(X)} -1 \right ] + {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$

In Exercise 3.2 the expected value ${\rm E} \big [\log_2 \hspace{0.05cm} {1}/{P_X(X)} \big ] =|X|$ was calculated for the case $p_\mu \ne 0$ for all $\mu$ . Thus, the first term disappears and the known result is obtained:

$$H(X) \le {\rm log}_2 \hspace{0.1cm}|X| \hspace{0.05cm}.$$

Hints:

The exercise belongs to the chapter Some preliminary remarks on 2D random variables.
In particular, reference is made to the page Probability function and entropy.
The same constellation is assumed here as in Exercise 3.2.

The equation of the binary entropy function is:

$$H_{\rm bin}(p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p} \hspace{0.05cm}.$$

Questions

Solution

(1) Both statements are correct:

If we set $p_3 = 0$ and formally $p_1 = p$ ⇒ $p_2 = 1- p$, we get the binary entropy function

$$H_{\rm bin}(p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p} \hspace{0.05cm}.$$

(2) Only the proposed solution 1 is correct:

One can also put the binary entropy function into the following form because of $\log(x) = \ln(x)/\ln(2)$ :

$$H_{\rm bin}(p) = \frac{-1}{{\rm ln}(2)} \cdot \big [ p \cdot {\rm ln}(p) + (1-p) \cdot {\rm ln}(1-p) \big ] \hspace{0.05cm}.$$

The first derivation leads to the result

$$\frac {{\rm d}H_{\rm bin}(p)}{{\rm d}p} = \frac{-1}{{\rm ln}(2)} \cdot \big [ {\rm ln}(p) + p \cdot \frac{1}{p} - {\rm ln}(1-p) - (1-p) \cdot \frac{1}{1-p} \big ] = \frac{1}{{\rm ln}(2)} \cdot \big [ {\rm ln}(1-p) - {\rm ln}(p) \big ] = {\rm log}_2 \hspace{0.1cm} \frac{1-p}{p} \hspace{0.05cm}.$$

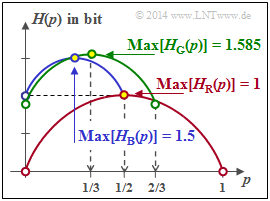
By setting this derivative to zero, we obtain the abscissa value $p = 0.5$, which leads to the maximum of the entropy function: $H_{\rm bin}(p =0.5) = 1$ bit
⇒ the proposed solution 2 is wrong.
By differentiating again, one obtains for the second derivative

$$\frac {{\rm d}^2H_{\rm bin}(p)}{{\rm d}p^2} = \frac{1}{{\rm ln}(2)} \cdot \left [ \frac{-1}{1-p} - \frac{1}{p} \right ] = \frac{-1}{{\rm ln}(2) \cdot p \cdot (1-p)} \hspace{0.05cm}.$$

This function is negative in the entire definition domain $0 ≤ p ≤ 1$ ⇒ $H_{\rm bin}(p)$ is concave ⇒ the proposed solution 1 is correct.

Three entropy functions with $M = 3$

(3) Propositions 1 and 2 are correct here:

For $p = 0$ one obtains the probability function $P_X(X) = \big [\hspace{0.05cm}0\hspace{0.05cm}, \hspace{0.15cm} 1/2\hspace{0.05cm},\hspace{0.15cm} 1/2 \hspace{0.05cm} \big ]$ ⇒ $H(X) = 1$ bit.
The maximum under the condition $p_3 = 1/2$ is obtained for $p_1 = p_2 = 1/4$:

$$P_X(X) = \big [\hspace{0.05cm}1/4\hspace{0.05cm}, \hspace{0.05cm} 1/4\hspace{0.05cm},\hspace{0.05cm} 1/2 \hspace{0.05cm} \big ] \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Max} \ [H_{\rm B}(p)] = 1.5 \ \rm bit \hspace{0.05cm}.$$

In compact form, $H_{\rm B}(p)$ with the constraint $0 ≤ p ≤ 1/2$ can be represented as follows:

$$H_{\rm B}(p) = 1.0\,{\rm bit} + {1}/{2} \cdot H_{\rm bin}(2p) \hspace{0.05cm}.$$

(4) The first and last statements are correct here::

The green curve with $p = 1/3$ also contains the equal distribution of all probabilities

$$ {\rm Max} \ [H_{\rm G}(p)] = \log_2 (3)\ \text{bit}.$$

In general, the entire curve in the range $0 ≤ p ≤ 2/3$ can be expressed as follows:

$$H_{\rm G}(p) = H_{\rm G}(p= 0) + {2}/{3} \cdot H_{\rm bin}(3p/2) \hspace{0.05cm}.$$

From the graph on the information page, one can also see that the following condition must be fulfilled:

$$H_{\rm G}(p = 0) + {2}/{3}= {\rm log}_2 \hspace{0.01cm} (3) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm G}(p= 0) = 1.585 - 0.667 = 0.918 \,{\rm bit} \hspace{0.05cm}.$$

The second suggested solution is therefore wrong. The same result can be obtained with the equation

$$H_{\rm G}(p = 0) = {1}/{3} \cdot {\rm log}_2 \hspace{0.01cm} (3) +{2}/{3} \cdot {\rm log}_2 \hspace{0.01cm} (3/2) = {\rm log}_2 \hspace{0.01cm} (3) -2/3 \cdot {\rm log}_2 \hspace{0.01cm} (2) \hspace{0.05cm}.$$

	$H_{\rm R}(p)$ results, for example, with $p_1 = p$, $p_2 = 1- p$ and $p_3 = 0$.
	$H_{\rm R}(p)$ is identical to the binary entropy function $H_{\rm bin}(p)$.

	$H_{\rm bin}(p)$ is concave with respect to the parameter $p$.
	$\text {Max } [H_{\rm bin}(p)] = 2$ bit applies.

	$H_{\rm B}(p)$ ergibt sich beispielsweise mit $p_1 = p$, $p_2 = 1/2- p$ und $p_3 = 1/2$.
	Es gilt $H_{\rm B}(p = 0)= 1$ bit.
	Es gilt $\text {Max } [H_{\rm B}(p)] = \log_2 \hspace{0.1cm} (3)$ bit.

	$H_{\rm G}(p)$ results, for example, with $p_1 = p$, $p_2 = 2/3- p$ and $p_3 = 1/3$.
	$H_{\rm G}(p = 0)= 1$ bit is valid.
	$\text {Max } [H_{\rm G}(p)] = \log_2 \hspace{0.1cm} (3)$ bit applies.