Exercise 3.7: Some Entropy Calculations

Diagram: Entropies and information

We consider the two random variables $XY$ and $UV$ with the following two-dimensional probability mass functions:

$$P_{XY}(X, Y) = \begin{pmatrix} 0.18 & 0.16\\ 0.02 & 0.64 \end{pmatrix}\hspace{0.05cm} \hspace{0.05cm}$$

$$P_{UV}(U, V) \hspace{0.05cm}= \begin{pmatrix} 0.068 & 0.132\\ 0.272 & 0.528 \end{pmatrix}\hspace{0.05cm}$$

For the random variable $XY$ the following are to be calculated in this task:

the joint entropy:

$$H(XY) = -{\rm E}\big [\log_2 P_{ XY }( X,Y) \big ],$$

the two individual entropies:

$$H(X) = -{\rm E}\big [\log_2 P_X( X)\big ],$$

$$H(Y) = -{\rm E}\big [\log_2 P_Y( Y)\big ].$$

From this, the following descriptive variables can also be determined very easily according to the above scheme – shown for the random variable $XY$:

the conditional entropies:

$$H(X \hspace{0.05cm}|\hspace{0.05cm} Y) = -{\rm E}\big [\log_2 P_{ X \hspace{0.05cm}|\hspace{0.05cm}Y }( X \hspace{0.05cm}|\hspace{0.05cm} Y)\big ],$$

$$H(Y \hspace{0.05cm}|\hspace{0.05cm} X) = -{\rm E}\big [\log_2 P_{ Y \hspace{0.05cm}|\hspace{0.05cm} X }( Y \hspace{0.05cm}|\hspace{0.05cm} X)\big ],$$

the mutual information between $X$ and $Y$:

$$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \cdot P_{Y}(Y) }\right ] \hspace{0.05cm}.$$

Finally, verify qualitative statements regarding the second random variable $UV$ .

Hints:

The exercise belongs to the chapter Different entropy measures of two-dimensional random variables.
In particular, reference is made to the pages
Conditional probability and conditional entropy as well as
Mutual information between two random variables.

Questions

$H(XY) \ = \ $

$\ \rm bit$

$H(X) \ = \ $

$\ \rm bit$

$H(Y) \ = \ $

$\ \rm bit$

$I(X; Y) \ = \ $

$\ \rm bit$

$H(X|Y) \ = \ $

$\ \rm bit$

$H(Y|X) \ = \ $

$\ \rm bit$

	The one-dimensional random variables $U$ and $V$ are statistically independent.
	The mutual information of $U$ and $V$ is $I(U; V) = 0$.
	For the compound entropy $H(UV) = H(XY)$ holds.
	The relations $H(U\|V) = H(U)$ and $H(V\|U) = H(V)$.

Solution

(1) From the given composite probability we obtain

$$H(XY) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.18} + 0.16\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.16}+ 0.02\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.02}+ 0.64\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.64} \hspace{0.15cm} \underline {= 1.393\,{\rm (bit)}} \hspace{0.05cm}.$$

(2) The one-dimensional probability functions are $P_X(X) = \big [0.2, \ 0.8 \big ]$ and $P_Y(Y) = \big [0.34, \ 0.66 \big ]$. From this follows:

$$H(X) = 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.8\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.8}\hspace{0.15cm} \underline {= 0.722\,{\rm (bit)}} \hspace{0.05cm},$$

$$H(Y) =0.34 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.34} + 0.66\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.66}\hspace{0.15cm} \underline {= 0.925\,{\rm (bit)}} \hspace{0.05cm}.$$

(3) From the graph on the information page you can see the relationship:

$$I(X;Y) = H(X) + H(Y) - H(XY) = 0.722\,{\rm (bit)} + 0.925\,{\rm (bit)}- 1.393\,{\rm (bit)}\hspace{0.15cm} \underline {= 0.254\,{\rm (bit)}} \hspace{0.05cm}.$$

(4) Similarly, according to the graph on the information page:

$$H(X \hspace{-0.1cm}\mid \hspace{-0.08cm} Y) = H(XY) - H(Y) = 1.393- 0.925\hspace{0.15cm} \underline {= 0.468\,{\rm (bit)}} \hspace{0.05cm},$$

$$H(Y \hspace{-0.1cm}\mid \hspace{-0.08cm} X) = H(XY) - H(X) = 1.393- 0.722\hspace{0.15cm} \underline {= 0.671\,{\rm (bit)}} \hspace{0.05cm}$$

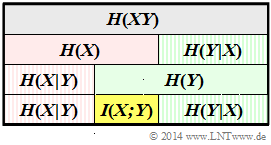
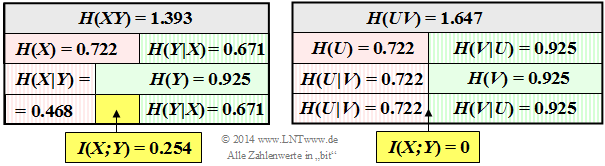
Entropy values for the random variables $XY$ and $UV$

The left diagram summarises the results of subtasks (1), ... , (4) true to scale.
The joint entropy is highlighted in grey and the mutual information in yellow.
A red background refers to the random variable $X$, and a green one to $Y$. Hatched fields indicate a conditional entropy.

The right graph describes the same situation for the random variable $UV$ ⇒ subtask (5).

(5) According to the diagram on the right, statements 1, 2 and 4 are correct:

One recognises the validity of $P_{ UV } = P_U · P_V$ ⇒ mutual information $I(U; V) = 0$ by the fact that the second row of the $P_{ UV }$ matrix differs from the first row only by a constant factor $(4)$ .
This results in the same one-dimensional probability functions as for the random variable $XY$ ⇒ $P_U(U) = \big [0.2, \ 0.8 \big ]$ and $P_V(V) = \big [0.34, \ 0.66 \big ]$.
Therefore $H(U) = H(X) = 0.722\ \rm bit$ and $H(V) = H(Y) = 0.925 \ \rm bit$.
Here, however, the following now applies for the joint entropy: $H(UV) = H(U) + H(V) ≠ H(XY)$.