Exercise 1.6Z: Interpretation of the Frequency Response

• Return to book

Impulse response and input signals

The task is to investigate the influence of a low-pass filter  $H(f)$  on cosinusoidal signals of the form

$$x_i(t) = A_x \cdot {\rm cos}(2\pi f_i t ).$$

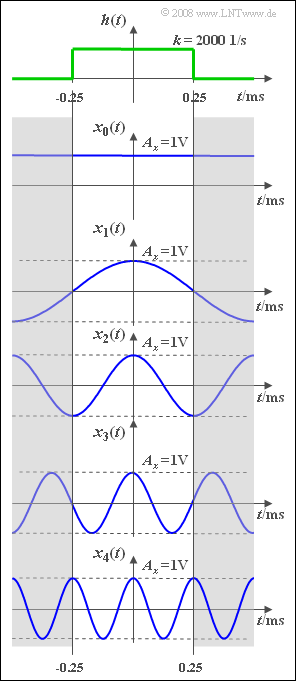
In the graph you can see the signals  $x_i(t)$, where the index $i$  indicates the frequency in $\rm kHz$ . So,  $x_2(t)$  describes a  $2 \hspace{0.09cm} \rm kHz$–signal.

The signal amplitude in each case is $A_x = 1 \hspace{0.05cm} \rm V$. The direct (DC) signal  $x_0(t)$  is to be interpreted as a limiting case of a cosine signal with frequeny  $f_0 =0$.

The upper sketch shows the rectangular impulse response  $h(t)$  of the low-pass filter. Its frequency response is:

$$H(f) = {\rm si}(\pi {f}/{ {\rm \Delta}f}) .$$

Due to linearity and the fact that $H(f)$  is real and even the output signals are also cosine-shaped:

$$y_i(t) = A_i \cdot {\rm cos}(2\pi f_i t ) .$$

• The signal amplitudes $A_i$  at the output for different frequencies  $f_i$ are searched-for and the solution is to be found in the time domain only.

• This somewhat circuitous solution is intended to make the basic relationship between the time and frequency domains clear.

Please note:

• The exercise belongs to the chapter  Some Low-Pass Functions in Systems Theory.
• Contrary to the usual definition of the amplitude, the "$A_i$" may well be negative. This corresponds then to the function „minus-cosine”.

Questions

1

Which low-pass filter is at hand here?

	Ideal low-pass filter,
	slit low-pass filter,
	Gaussian low-pass filter.

2

State the equivalent bandwidth of  $H(f)$ .

$\Delta f \ =\ $ $\ \rm kHz$

3

In general, compute the amplitude  $A_i$  as a function of  $x_i(t)$  and  $h(t)$. Which of the following should be considered in the calculations?

	For the cosine signal,  $A_i = y_i(t = 0)$ holds.
	The following holds:  $y_i(t) = x_i(t) · h(t)$.
	The following holds:  $y_i(t) = x_i(t) ∗ h(t)$.

4

Which of the following results are true for  $A_0, A_2$  and  $A_4$ ?   The following still holds:   $A_i = y_i(t = 0)$.

	$A_0 = 0$.
	$A_0 = 1 \hspace{0.05cm} \rm V $.
	$A_2 = 0$.
	$A_2 = 1 \hspace{0.05cm} \rm V $.
	$A_4 = 0$.
	$A_4 =1 \hspace{0.05cm} \rm V $.

5

Compute the amplitudes  $A_1$  and  $A_3$  for a  $1 \ \rm kHz$– and  $3 \ \rm kHz$–signal.
Interpret the results using the spectral functions.

$A_1 \ = \ $ $\ \rm V$

$A_3 \ = \ $ $\ \rm V$

Solution

Solution

(1)  Approach 2 is correct:   It is a slit low-pass filter.

(2)  The (equivalent) time duration of the impulse response is  $Δt = 0.5 \ \rm ms$.   The equivalent bandwidth is equal to the reciprocal:

$$Δf = 1/Δt \ \rm \underline{= \ 2 \ kHz}.$$

(3)  Approaches 1 and 3 are correct:

• The amplitude is  $A_i = y_i(t = 0)$ since  $y_i(t)$  is cosine-shaped. The output signal is calculated by convolution for this purpose:

$$A_i = y_i (t=0) = \int\limits_{ - \infty }^{ + \infty } {x_i ( \tau )} \cdot h ( {0 - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$

• Considering the symmetry and the time limitation of  $h(t)$ the following result is obtained:

$$A_i = \frac{A_x}{\Delta t} \cdot \int\limits_{ - \Delta t /2 }^{ + \Delta t /2 } {\rm cos}(2\pi f_i \tau )\hspace{0.1cm}{\rm d}\tau.$$

(4)  Approaches 2, 3 and 5 are correct:

• Beim Gleichsignal  $x_0(t) = A_x$  ist  $f_i = 0$  zu setzen und man erhält  $A_0 = A_x \ \rm \underline{ = \ 1 \hspace{0.05cm} V}$.
• Dagegen verschwindet bei den Cosinusfrequenzen  $f_2 = 2 \ \rm kHz$  und  $f_4 = 4 \ \rm kHz$  jeweils das Integral, da dann genau über eine bzw. zwei Periodendauern zu integrieren ist:   $A_2 \ \rm \underline{ = \hspace{0.05cm} 0}$  und  $A_4 \hspace{0.05cm} \rm \underline{ = \ 0}$.
• Im Frequenzbereich entsprechen die hier behandelten Fälle:

$$H(f=0) = 1, \hspace{0.3cm}H(f=\Delta f) = 0, \hspace{0.3cm}H(f=2\Delta f) = 0.$$

(5)  Das Ergebnis der Teilaufgabe  (3)  lautet unter Berücksichtigung der Symmetrie für  $f_i = f_1$:

$$A_1= \frac{2A_x}{\Delta t} \cdot \int\limits_{ 0 }^{ \Delta t /2 } {\rm cos}(2\pi f_1 \tau )\hspace{0.1cm}{\rm d}\tau = \frac{2A_x}{2\pi f_1 \cdot \Delta t} \cdot {\rm sin}(2\pi f_1 \frac{\Delta t}{2} )= A_x \cdot {\rm si}(\pi f_1 \Delta t ).$$

• Mit  $f_1 · Δt = 0.5$  lautet somit das Ergebnis:

$$A_1 = A_x \cdot {\rm si}(\frac{\pi}{2} ) = \frac{2A_x}{\pi} \hspace{0.15cm}\underline{= 0.637\,{\rm V}}.$$

• Entsprechend erhält man mit  $f_3 · Δt = 1.5$:

$$A_3 = A_x \cdot {\rm si}({3\pi}/{2} ) = -\frac{2A_x}{3\pi} = -{A_1}/{3}\hspace{0.15cm}\underline{= -0.212\,{\rm V}}.$$

• Genau zu den gleichen Ergebnissen – aber deutlich schneller – kommt man durch die Anwendung der Gleichung:

$$A_i = A_x · H(f = f_i).$$

• Bereits aus den Grafiken auf der Angabenseite erkennt man, dass das Integral über  $x_1(t)$  im markierten Bereich positiv und das Integral über  $x_3(t)$  negativ ist.
• Es ist allerdings anzumerken, dass man im Allgemeinen als Amplitude meist den Betrag bezeichnet (siehe Hinweis auf der Angabenseite).