Exercise 1.2: Entropy of Ternary Sources

• Return to book

Probabilities of two ternary sources

The entropy of a discrete memoryless source with  $M$  possible symbols is:

$$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} {\rm pseudo unit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$

Here, the  $p_\mu$  denote the occurrence probabilities of the individual symbols or events.  In the present example, the events are denoted by  $\rm R$(ed),  $\rm G$(reen)  and  $\rm S$(chwarz)  with  "Schwarz"  being the German word for  "Black".

• For a binary source with the occurrence probabilities  $p$  and  $1-p$  this can be written:

$$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm},\hspace{0.3cm} \text{pseudo–unit: bit}\hspace{0.05cm}.$$

• The entropy of a multilevel source can often be expressed with this  "binary entropy function"  $H_{\rm bin}(p)$.

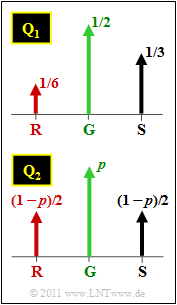
In this task, two ternary sources with the symbol probabilities according to the above graph are considered:

1. source  $\rm Q_1$ with  $p_{\rm G }= 1/2$,  $p_{\rm S }= 1/3$  and  $p_{\rm R }= 1/6$,
2. source  $\rm Q_2$ with  $p_{\rm G }= p$  and  $p_{\rm S } = p_{\rm R } = (1-p)/2$.

• The ternary source  $\rm Q_2$  can also be applied to  "Roulette"  when a player bets only on the squares  $\rm R$(ed),  $\rm S$(chwarz)  and $\rm G$(reen)  (the "zero").  This type of game is referred to as  $\text{Roulette 1}$  in the question section.

• In contrast,  $\text{Roulette 2}$  indicates that the player bets on single numbers  $(0$, ... , $36)$.

Hint:

• The task belongs to the chapter  Discrete Memoryless Sources.

Questions

1

What is the entropy  $H$  of the source  $\rm \underline{Q_1}$?

$H \ = \ $ $\ \rm bit$

2

Which of the following statements are true if  $\rm R$,  $\rm G$  and  $\rm S$  are represented by the numerical values  $-1$,  $0$  and  $+1$ ?

	The result is a smaller entropy.
	The entropy remains the same.
	The result is a greater entropy.

3

Determine the entropy of the source  $\rm \underline{Q_2}$  using the binary entropy function  $H_{\rm bin}(p)$.  What value results for  $\underline{p = 0.5}$?

$H \ = \ $ $\ \rm bit$

4

For which  $p$–value of the source  $\rm \underline{Q_2}$  does the maximum entropy result:  $H → H_\text{max}$?

$p \ = \ $

5

What is the entropy of the source model  $\text{Roulette 1}$,  i.e. with respect to the events  $\rm R$(ed),  $\rm S$(chwarz)  and  $\rm G$(reen)  (the "zero")?

$H \ = \ $ $\ \rm bit$

6

What is the entropy of  $\text{Roulette 2}$ ,  i.e. with regard to the numbers   $0$, ... , $36$?

$H \ = \ $ $\ \rm bit$

Solution

Solution

(1)  With the "symbol" probabilities  $1/2$,  $1/3$  and  $1/6$  we get the following entropy value:

$$H \hspace{0.1cm} = \hspace{0.1cm} 1/2 \cdot {\rm log}_2\hspace{0.1cm}(2) +1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) +1/6 \cdot {\rm log}_2\hspace{0.1cm}(6) =(1/2 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(2) + (1/3 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(3) \hspace{0.15cm}\underline {\approx 1.46 \, {\rm bit}} \hspace{0.05cm}.$$

(2) Proposed solution 2 is correct:

• The entropy depends only on the probabilities of occurrence.
• It does not matter which numerical values or physical quantities one assigns to the individual symbols.
• It is different with mean values or the ACF (auto correlation function) calculation.  If only symbols are given, no moments can be calculated for them.
• Moreover, the mean values, auto-correlation, etc. depend on whether one agrees on the assignment bipolar  $(-1, \hspace{0.10cm}0, \hspace{0.05cm}+1)$  or unipolar  $(0, \hspace{0.05cm}1, \hspace{0.05cm}2)$ .

(3)  The entropy of source  $\rm Q_2$  can be expressed as follows:

$$H \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ 2 \cdot \frac{1-p}{2} \cdot {\rm log}_2\hspace{0.1cm}\frac {2}{1-p}= p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{1-p} + (1-p)\cdot {\rm log}_2\hspace{0.1cm}(2)= H_{\rm bin}(p) + 1-p \hspace{0.05cm}.$$

• For  $p = 0.5$   ⇒   $H_{\rm bin}(p) = 1$ , we get  $\underline{H = 1.5\hspace{0.05cm}\rm bit}$.

(4)  The maximum entropy of a memoryless source with symbol set size  $M$  is obtained when all  $M$  symbols are equally probable.

• For the special case  $M=3$  it follows:

$$p_{\rm R} + p_{\rm G} + p_{\rm S} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {p = 1/3 \approx 0.333}\hspace{0.05cm}.$$

• Thus, using the result of sub-task  (3) , we obtain the following entropy:

$$H = H_{\rm bin}(1/3) + 1-1/3 = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3/2) + 2/3 $$

$$\Rightarrow \hspace{0.3cm}H = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3) - 2/3 \cdot {\rm log}_2\hspace{0.1cm}(2)+ 2/3 = {\rm log}_2\hspace{0.1cm}(3) = {1.585 \, {\rm bit}} \hspace{0.05cm}.$$

(5)  The source model  $\text{Roulette 1}$  is information theoretically equal to the configuration  $\rm Q_2$  with  $p = 1/37$:

$$p_{\rm G} = p = \frac{1}{37}\hspace{0.05cm},\hspace{0.2cm} p_{\rm R} = p_{\rm S} = \frac{1-p}{2} = \frac{18}{37} \hspace{0.05cm}.$$

• Thus, using the result of subtask  (3), we obtain:

$$H = H_{\rm bin}(1/37) + \frac{36}{37} = \frac{1}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) - \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}36 + \frac{36}{37} = {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot ( 1- {\rm log}_2\hspace{0.1cm}(36)) = 5.209 - 4.057 \hspace{0.15cm} \underline { = 1.152 \, {\rm bit}} \hspace{0.05cm}.$$

(6)  If we bet on single numbers in roulette   ⇒   source model  $\text{Roulette 2}$, all numbers from  $0$  to  $36$  are equally probable and we get:

$$H = {\rm log}_2\hspace{0.1cm}(37) \hspace{0.15cm} \underline { = 5.209 \, {\rm bit}} \hspace{0.05cm}.$$