Exercise 1.3: System Comparison at AWGN Channel
For the comparison of different modulation and demodulation methods with regard to noise sensitivity, we usually start from the so-called AWGN Channel and present the following double logarithmic diagram:
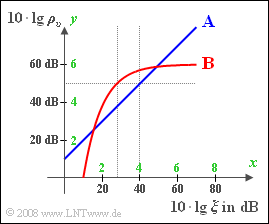
- The y-axis indicates the sinkt-to-noise ratio (logarithmic SNR) $10 · \lg ρ_v$ in dB.
- $10 · \lg ξ$ is plotted on the x-axis; the normalized power parameter ("performance parameter") is characterized by:
- $$ \xi = \frac{P_{\rm S} \cdot \alpha_{\rm K}^2 }{{N_0} \cdot B_{\rm NF}}\hspace{0.05cm}.$$
- Thus, the transmission $P_{\rm S}$, the channel attenuation factor $α_{\rm K}$, the noise power density $N_0$ and the bandwidth $B_{\rm NF}$ of the message signal are suitably summarised together in $ξ$ .
- Unless explicitly stated otherwise, the following values shall be assumed in the exercise:
- $$P_{\rm S}= 5 \;{\rm kW}\hspace{0.05cm}, \hspace{0.2cm} \alpha_{\rm K} = 0.001\hspace{0.05cm}, \hspace{0.2cm} {N_0} = 10^{-10}\;{\rm W}/{\rm Hz}\hspace{0.05cm}, \hspace{0.2cm} B_{\rm NF}= 5\; {\rm kHz}\hspace{0.05cm}.$$
Two systems are plotted in the graph and their $(x, y)$-curve can be described as follows:
- $\text{System A}$ is characterized by the following equation:
- $$y = x+1.$$
- Accordingly, $\text{System B}$ is characterized by:
- $$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right)\hspace{0.05cm}.$$
The additional axis labels drawn in green have the following meaning:
- $$ x = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\xi} {10 \,{\rm dB}}\hspace{0.05cm}, \hspace{0.3cm}y = \frac{10 \cdot {\rm lg} \hspace{0.1cm}\rho_v} {10 \,{\rm dB}}\hspace{0.05cm}.$$
Thus $x = 4$ represents $10 · \lg ξ = 40\text{ dB}$ or $ξ = 10^4$ and $y = 5$ represents $10 · \lg ρ_v= 50\text{ dB}$ , i.e., $ρ_v = 10^5$.
Hints:
- This exercise belongs to the chapter Quality Criteria.
- Particular reference is made to the page Investigating at the AWGN Channel.
- By specifying the powers in watts, they are independent of the reference resistance, 𝑅. $R$.
Questions
Solution
- $$\xi = \frac{5 \cdot 10^3\,{\rm W}\cdot 10^{-6} }{10^{-10}\,{\rm W}/{\rm Hz} \cdot 5 \cdot 10^3\,{\rm Hz}} = 10^4 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = 40\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x=4 \hspace{0.05cm}.$$
- This gives the auxiliary coordinate value $y = 5$, which leads to a sink-to-noise ratio of $10 · \lg \hspace{0.05cm} ρ_v\hspace{0.15cm}\underline{ = 50 \ \rm dB}$ .
(2) Answers 2 and 3 are correct:
This requirement corresponds to a $10$ dB, increase in the signal-to-noise ratio compared to the previous system, so $10 · \lg \hspace{0.05cm}ξ$ must also be increased by $10$ dB:
- $$10 \cdot {\rm lg} \hspace{0.1cm}\xi = 50\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \xi=10^5 \hspace{0.05cm}.$$
A tenfold larger $ξ$ value is achieved – provided all other parameters are held constant in each case –
- by a transmission power of $P_{\rm S} = 50$ kW instead of $5$ kW,
- by a channel transmission factor of $α_{\rm K} = 0.00316$ instead of $0.001$,
- by a noise power density of $N_0 = 10^{ –11 }$ W/Hz instead of $10^{ –10 }$ W/Hz,
- by a bandwidth of $B_{\rm NF} = 0.5$ kHz instead of $5$ kHz.
(3) Für $10 · \lg \hspace{0.05cm} ξ = 40$ dB ist die Hilfsgröße $x = 4$. Damit ergibt sich für die Hilfsgröße der Ordinate:
- $$y= 6 \cdot \left(1 - {\rm e}^{-3} \right)\approx 5.7 \hspace{0.05cm}.$$
- Dies entspricht dem Sinken–Störabstand $10 · \lg \hspace{0.05cm} ρ_v\hspace{0.15cm}\underline{ = 57 \ \rm dB}$, also einer Verbesserung gegenüber dem $\text{System A}$ um $7$ dB.
(4) Diese Problemstellung wird durch folgende Gleichung beschrieben:
- $$ y= 6 \cdot \left(1 - {\rm e}^{-x+1} \right) = 5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm e}^{-x+1} ={1}/{6}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} x = 1+ {\rm ln} \hspace{0.1cm}6 \approx 2.79 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = 27.9\,{\rm dB}\hspace{0.05cm}.$$
- Bei $\text{System A}$ war hierfür $10 · \lg \hspace{0.05cm} \xi = 40$ dB notwendig, was bei den weiter gegebenen Zahlenwerten durch $P_{\rm S} = 5$ kW erreicht wurde.
- Nun kann die Sendeleistung um etwa $12.1$ dB verringert werden:
- $$ 10 \cdot {\rm lg} \hspace{0.1cm} \frac{P_{\rm S}}{ 5 \;{\rm kW}}= -12.1\,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{P_{\rm S}}{ 5 \;{\rm kW}} = 10^{-1.21}\approx 0.06\hspace{0.05cm}.$$
- Das bedeutet: Bei $\text{System B}$ wird mit nur $6\%$ der Sendeleistung von $\text{System A}$ – also mit nur $P_{\rm S} \hspace{0.15cm}\underline{ = 0.3 \ \rm kW}$ – die gleiche Systemqualität erzielt.
(5) Wir bezeichnen mit $V$ (steht für "Verbesserung") den größeren Sinken–Störabstand von $\text{System B}$ gegenüber $\text{System A}$ :
- $$V = 10 \cdot {\rm lg} \hspace{0.1cm}\rho_v \hspace{0.1cm}{\rm (System\;B)} - 10 \cdot {\rm lg} \hspace{0.1cm}\rho_v \hspace{0.1cm}{\rm (System\;A)} = \left[6 \cdot \left(1 - {\rm e}^{-x+1} \right) -x -1 \right] \cdot 10\,{\rm dB}\hspace{0.05cm}.$$
- Durch Nullsetzen der Ableitung ergibt sich derjenige $x$–Wert, der zur maximalen Verbesserung führt:
- $$ \frac{{\rm d}V}{{\rm d}x} = 6 \cdot {\rm e}^{-x+1} -1\Rightarrow \hspace{0.3cm} x = 1+ {\rm ln} \hspace{0.1cm}6 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm}\xi = \hspace{0.15cm}\underline {27.9\,{\rm dB}}\hspace{0.05cm}.$$
- Es ergibt sich also genau der in der Teilaufgabe (4) behandelte Fall mit $10 · \lg ρ_υ = 50$ dB, während der Störabstand bei $\text{System A}$ nur $37.9$ dB beträgt.
- Die Verbesserung ist demnach $12.1$ dB.