Exercise 2.11: Envelope Demodulation of an SSB Signal

(Normalized) envelope in
Single-sideband modulation

Let us consider the transmission of the cosine signal

$$ q(t) = A_{\rm N} \cdot \cos(\omega_{\rm N} \cdot t)$$

according to the modulation method "USB–AM with carrier". At the receiver, the high frequency is reset to the LF range with an envelope demodulator .

The channel is assumed to be ideal such that the received signal $r(t)$ is identical to the transmit signal $s(t)$ . With a sideband-to-carrier ratio

$$ \mu = \frac{A_{\rm N}}{2 \cdot A_{\rm T}}$$

the equivalent lowpass signal can be written as:

$$r_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + \mu \cdot {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right) \hspace{0.05cm}$$

The envelope – i.e., the magnitude of this complex signal – can be determined by geometric considerations. Independent of the parameter $μ$, one obtains:

$$a(t ) = A_{\rm T} \cdot \sqrt{1+ \mu^2 + 2 \mu \cdot \cos(\omega_{\rm N} \cdot t)}\hspace{0.05cm}.$$

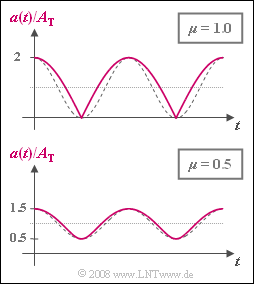
The time-independent envelope $a(t)$ for $μ = 1$ and $μ = 0.5$ is shown in the graph. In each case, the amplitude-matched cosine oscillations, which would be a prerequisite for distortion-free demodulation, are plotted as dashed comparison curves.

The periodic signal $a(t)$ can be approximated by a Fourier Series :

$$a(t ) = A_{\rm 0} + A_{\rm 1} \cdot \cos(\omega_{\rm N} \cdot t) + A_{\rm 2} \cdot \cos(2\omega_{\rm N} \cdot t)+ A_{\rm 3} \cdot \cos(3\omega_{\rm N} \cdot t)\hspace{0.05cm}+\text{...}$$

The Fourier coefficients were determined using a simulation program. With $μ = 1$ the following values were obtained:

$$A_{\rm 0} = 1.273\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.849\,{\rm V},\hspace{0.3cm}A_{\rm 2} = -0.170\,{\rm V},\hspace{0.3cm} A_{\rm 3} = 0.073\,{\rm V},\hspace{0.3cm}A_{\rm 4} = 0.040\,{\rm V} \hspace{0.05cm}.$$

Accordingly, for $μ = 0.5$, the simulation yielded:

$$A_{\rm 0} = 1.064\,{\rm V},\hspace{0.3cm} A_{\rm 1} = 0.484\,{\rm V},\hspace{0.3cm}A_{\rm 2} = 0.058\,{\rm V} \hspace{0.05cm}.$$

The values not given here can be ignored when calculating of the distortion factor.

The sink signal $v(t)$ is obtained from $a(t)$ as follows:

$$v(t) = 2 \cdot \big [a(t ) - A_{\rm 0} \big ] \hspace{0.05cm}.$$

The factor of $2$ corrects for the amplitude loss due to SSB-AM, while the subtraction of the DC signal coefficient $A_0$ takes into account the influence of the high-pass within the envelope demodulator.

In questions (1) to (3) , it is assumed that $A_{\rm N} = 2 \ \rm V$, $A_{\rm T} = 1 \ \rm V$ ⇒ $μ = 1$ , whereas from question (4) , $A_{\rm N} = A_{\rm T} = 1 \ \rm V$ should apply for the parameter $μ = 0.5$.

Hints:

This exercise belongs to the chapter Single-Sideband Modulation.
Particular reference is made to the page Sideband-to-carrier ratio.
Also compare your results to the rule of thumb which states that for the envelope demodulation of an SSB-AM signal with sideband-to-carrier ratio $μ$ , the distortion factor is $K ≈ μ/4$ .

Questions

$v_{\rm max} \ = \ $

$\ \rm V$

$v_{\rm min} \ = \ $

$\ \rm V$

$K \ = \ $

$\ \text{%}$

	The lower cosine half-wave is more peaked than the upper one.
	The DC component ${\rm Ε}\big[v(t)\big ] = 0$.

$v_{\rm max} \ = \ $

$\ \rm V$

$v_{\rm min} \ = \ $

$\ \rm V$

$K \ = \ $

$\ \text{%}$

$K_{\rm max} \ = \ $

$\ \text{%}$

Solution

(1) The maximum value $a_{\rm max} = 2\ \rm V$ and the minimum value $a_{\rm min} = 0$ can be read of the graph or calculated using the equation given:

$$ a_{\rm max} = A_{\rm T} \cdot \sqrt{1+ \mu^2 + 2 \mu}= A_{\rm T} \cdot (1+ \mu) = 2\,{\rm V} \hspace{0.05cm},$$

$$a_{\rm min} = A_{\rm T} \cdot \sqrt{1+ \mu^2 - 2 \mu}= A_{\rm T} \cdot (1- \mu) = 0 \hspace{0.05cm}.$$

For the two extreme values of the sink signal it follows:

$$ v_{\rm max} = 2 \cdot [a_{\rm max} - A_{\rm 0}] = 2 \cdot [2\,{\rm V} - 1.273\,{\rm V}] \hspace{0.15cm}\underline {=1.454\,{\rm V}}\hspace{0.05cm},$$

$$ v_{\rm min} = -2 \cdot A_{\rm 0} \hspace{0.15cm}\underline {= -2.546\,{\rm V}}\hspace{0.05cm}.$$

(2) Ignoring the Fourier coeffizients $A_5$, $A_6$, etc., we obtain:

$$K = \frac{\sqrt{A_2^2 + A_3^2+ A_4^2 }}{A_1}= \frac{\sqrt{0.170^2 + 0.073^2 + 0.040^2 }{\,\rm V}}{0.849\,{\rm V}}\hspace{0.15cm}\underline { \approx 22.3 \%}.$$

Here, the approximation $K ≈ μ/4$ yields the value $25\%$.

(3) Only the first answer is correct.

Due to the high-pass within the envelope demodulator, the DC signal component would also be equal to zero if no distortions were present.

(4) Like in subtask (1) here it holds that:

$$v_{\rm max} = 2 \cdot [a_{\rm max} - A_{\rm 0}] = 2 \cdot [1.5\,{\rm V} - 1.064\,{\rm V}] \hspace{0.15cm}\underline {= 0.872\,{\rm V}}\hspace{0.05cm},$$

$$ v_{\rm min} = -2 \cdot A_{\rm 0} \hspace{0.15cm}\underline {= -2.128\,{\rm V}}\hspace{0.05cm}.$$

(5) A smaller sideband-to-carrier ratio also results in a smaller distortion factor:

$$K = \frac{0.058{\,\rm V}}{0.484\,{\rm V}}\hspace{0.15cm}\underline { \approx 12 \%}.$$

The simple approximation $K ≈ μ/4$ here yields $12.5\%$.
It can be concluded that the above rule of thumb is more accurate for smaller values of $μ$ .

(6) Thus, the distortion factor is largest when one of the sidebands is entirely cut out.

However, since the envelope demodulator has no information to distinguish between
- a SSB–AM, or
- a SSB-AM which has been extremely affected by the channel,

$K_{\rm max} ≈ μ/4$ simultaneously provides an upper bound for the DSB-AM.

A comprison of the parameters $m = A_{\rm N}/A_{\rm T}$ and $μ = A_{\rm N}/(2A_{\rm T})$ leads to the result:

$$K_{\rm max} = \frac{\mu}{4} = \frac{m}{8} \hspace{0.15cm}\underline {=6.25 \%}.$$