Exercise 5.9: Minimization of the MSE

Power-spectral densities
with the Wiener filter

Given a stochastic useful signal $s(t)$ of which only the power-spectral density (PSD) is known:

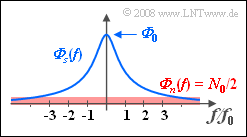
$${\it \Phi} _s (f) = \frac{\it{\Phi} _{\rm 0} }{1 + ( {f/f_0 } )^2 }.$$

This power-spectral density ${\it \Phi} _s (f)$ is shown in blue in the accompanying diagram.

The average power of $s(t)$ is obtained by integration over the power-spectral density:

$$P_s = \int_{ - \infty }^{ + \infty } {{\it \Phi} _s (f)}\, {\rm d} f = {\it \Phi} _0 \cdot f_0 \cdot {\rm{\pi }}.$$

Additively superimposed on the useful signal $s(t)$ is white noise $n(t)$ with noise power density ${\it \Phi}_n(f) = N_0/2.$
As an abbreviation, we use $Q = 2 \cdot {\it \Phi}_0/N_0$, where $Q$ could be interpreted as "quality".
Note that $Q$ does not represent a signal–to–noise power ratio.

In this exercise, we want to determine the frequency response $H(f)$ of a filter that minimizes the mean square error $\rm (MSE)$ between the useful signal $s(t)$ and the filter output signal $d(t)$:

$${\rm{MSE}} = \mathop {\lim }\limits_{T_{\rm M} \to \infty } \frac{1}{T_{\rm M} }\int_{ - T_{\rm M} /2}^{T_{\rm M} /2} {\left| {d(t) - s(t)} \right|^2 \, {\rm{d}}t.}$$

Notes:

The exercise belongs to the chapter Wiener–Kolmogorow Filter.

The following indefinite integral is given for solving:

$$\int {\frac{1}{a^2 + x^2 }} \, {\rm{d}}x ={1}/{a} \cdot \arctan \left( {{x}/{a}} \right).$$

Questions

	$H(f)$ is a Gaussian low pass.
	$H(f)$ represents a matched filter.
	$H(f)$ represents a Wiener–Kolmogorov filter.

$H(f = 0) \ = \ $

$H(f = 2f_0)\ = \ $

${\rm MSE}/P_s \ = \ $

$Q_\text{min} \ = \ $

	A filter of the same shape $H(f) = K \cdot H_{\rm WF}(f)$ leads to the same result.
	The output signal $d(t)$ contains more higher frequency components when $Q$ is larger.

Solution

(1) Only the last solution is correct:

The task ⇒ "Minimization of the mean square error" already points to the–Kolmogorow filter.
The matched filter, on the other hand, is used to concentrate the signal energy and thereby maximize the S/N ratio for a given time.

(2) For the optimal frequency response, according to Wiener and Kolmogorov, the following applies in general:

$$H(f) = H_{\rm WF} (f) = \frac{1}{{1 + {\it \Phi} _n (f)/{\it \Phi} _s (f)}}.$$

With the given power-spectral density, it is also possible to write for this:

$$H(f) = \frac{1}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} = \frac{1}{{1 + {1}/{Q}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}}.$$

With $Q = 3$ it follows:

$$H( {f = 0} ) = \frac{1}{{1 + {1}/{Q}}} = \frac{Q}{Q + 1} \hspace{0.15cm}\underline {= 0.75},$$

$$H( {f = 2f_0 } ) = \frac{1}{{1 + {5}/{Q}}} = \frac{Q}{Q + 5} \hspace{0.15cm}\underline {= 0.375}.$$

(3) For the filter calculated in subtask (2), taking symmetry into account, the following holds:

$${\rm{MSE = }}\int_{-\infty}^{+\infty} H(f) \cdot {\it \Phi} _n (f) \,\, {\rm{d}}f = \int_{0}^{+\infty} \frac{N_0}{{1 + {N_0 }/({{2{\it \Phi} _0 })}\cdot \left[ {1 + ( {f/f_0 } )^2 } \right]}} \,\, {\rm{d}}f .$$

For this, with $Q = 2 \cdot {\it \Phi}_0/N_0$ and $a^2 = Q + 1$, we can also write:

$${\rm{MSE = }}\int_0^\infty {\frac{{2{\it \Phi} _0 }}{{ Q+1 + ( {f/f_0 })^2 }}} \,\, {\rm{d}}f = 2{\it \Phi} _0 \cdot f_0 \int_0^\infty {\frac{1}{a^2 + x^2 }}\,\, {\rm{d}}x.$$

With the integral given, this leads to the result:

$${\rm{MSE}} = \frac{{2{\it \Phi} _0 f_0 }}{{\sqrt {1 + Q} }}\left( {\arctan ( \infty ) - \arctan ( 0 )} \right) = \frac{{{\it \Phi} _0 f_0 {\rm{\pi }}}}{{\sqrt {1 + Q} }}.$$

Normalizing MSE to the useful power $P_s$, we obtain for $Q=3$:

$$\frac{\rm{MSE}}{P_s} = \frac{1}{{\sqrt {1 + Q} }} \hspace{0.15cm}\underline { = 0.5}.$$

(4) From the calculation in subtask (3), the condition $Q \ge 99$ ⇒ $Q_{\rm min} \hspace{0.15cm}\underline{= 99}$ follows directly for ${\rm MSE}/P_s \ge 0.1.$

The larger $Q$ is, the smaller the mean square error becomes.

(5) Only the second solution is correct:

A frequency response of the same shape as the Wiener–Kolmogorov filter ⇒ $H(f) = K \cdot H_{\rm WF}(f)$ with $K \ne 1$ always leads to large distortions.
This can be illustrated, for example, by the noise-free case $(Q \to \infty)$. In this case, $d(t) = K \cdot s(t)$ and the optimization task would be extremely poorly solved despite good conditions.
From the equation

$${\rm{MSE}} = \int_{ - \infty }^{ + \infty } {H_{\rm WF} (f)} \cdot \it{\Phi} _n (f)\,\,{\rm{d}}f$$

one might incorrectly conclude that a filter $H(f) = 2 \cdot H_{\rm WF}(f)$ only doubles the mean squared error.

However, this is not the case, since $H(f)$ is then no longer a Wiener filter and the above equation is also no longer applicable.

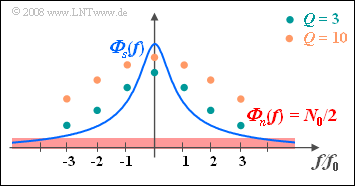
Power-spectral density with the Wiener filter

The second statement is true, as can be seen from the accompanying diagram.

The dots mark the frequency response $H_{\rm WF}(f))$ of the Wiener–Kolmogorow filter for $Q = 3$ and for $Q = 10$, respectively.
For larger $Q (= 10)$, high components are attenuated less than for lower $Q (= 3)$.
Therefore, in the case of $Q = 10$, the filter output signal also contains more higher frequency components, which are due to the noise $n(t)$.