Exercise 4.1Z: Appointment to Breakfast

• Return to book

Candidates for Chancellor having breakfast in 2002

Ms. M. and Mr. S. are known to meet often for a joint breakfast:

• Both promise to come to such a meeting on a certain day between 8 am and 9 am.
• Further, they agree that each of them will arrive in this period (and only in this period) on "good luck" and wait up to fifteen minutes for the other.

Hints:

• The task belongs to the chapter  Two-Dimensional Random Variables.

• Use the minute of arrival time as the time in the following questions: 
  "Minute = 0" stands for 8 o'clock, "Minute = 60" for 9 o'clock.
• The task arose before the 2002 Bundestag elections, when both Dr. Angela Merkel and Dr. Edmund Stoiber wanted to become the CDU/CSU's candidate for chancellor.
• At a joint breakfast in Wolfratshausen, Mrs. Merkel renounced.  The later election was won by Gerhard Schröder (SPD).

Questions

1

What is the probability $p_1$ that the two will meet when Mr. S. arrives at 8:30? Give reasons for your answer.

$p_1 \ = \ $ $\ \%$

2

Which arrival time should Ms. M. choose if she does not actually want to meet Mr. S., but still wants to keep to the agreement made?
What is the probability $p_2$ that Ms. M. and Mr. S. will meet?

$p_2 \ = \ $ $\ \%$

3

Which arrival time should Ms. M. choose if she not only wants to avoid a meeting as much as possible, but also wants to minimize the waiting time?

$\rm minute \ = \ $

4

What is the probability  $p_4$  for a meeting in general, that is, if both actually appear on "Gut Glück"?

$p_4 \ = \ $ $\ \%$

Solution

Solution

(1)  If Mr. S. arrives at 8:30, he will meet Mrs. M. if she arrives between 8:15 and 8:45. Thus the probability

$$p_1 = \text{Pr(Mr. S. meets Ms. M.)}\hspace{0.15cm}\underline{=50\%}.$$

"Favorable area" for meeting

(2)  If Ms. M. arrives at 8 a.m., she meets Mr. S. only if he arrives before 8:15.

• If Mrs. M. arrives at 9 a.m., Mr. S. must arrive after 8:45 a.m. so that they can meet.
• The probability of meeting is the same in both cases:

$$p_2 = \big[\text{Min Pr(Mr. S. meets Ms. M.)}\big]\hspace{0.15cm}\underline{=25\%}.$$

(3)  Of the two arrival times calculated in (2), 9 o'clock  $(\underline{\text{Minute = 60}})$  is more favorable,
      since she – if Mr. S. is not there – can leave immediately.

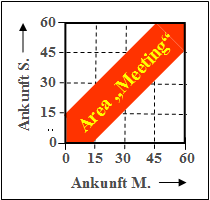
(4)  The probability  $p_4$  is given as the ratio of the red area in the graph to the total area  $1$.

• Using the triangular areas, one obtains:

$$p_4=\rm 1-2\cdot\frac{1}{2}\cdot\frac{3}{4}\cdot\frac{3}{4}=\frac{7}{16}\hspace{0.15cm}\underline{=\rm 43.75\%}.$$