Exercise 2.1Z: About the Equivalent Bitrate

• Return to book

Source signal (top) and encoder signal (bottom)

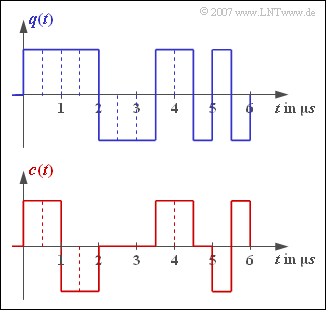
The upper diagram shows the source signal  $q(t)$  of a redundancy-free binary source with bit duration  $T_{q}$  and  bit rate $R_{q}$. The two signal parameters  $T_{q}$  and  $R_{q}$  can be taken from the sketch.

• This binary signal is coded symbol-by-symbol and results in the encoder signal  $c(t)$ drawn below.
• All possible encoder symbols occur in the signal section of duration  $6 \ \rm µ s$  shown.
• The level number  $M_{c}$  and the symbol duration  $T_{c}$  can be used to specify the equivalent bit rate of the encoder signal:

$$R_c = \frac{{\rm log_2} (M_c)}{T_c} \hspace{0.05cm}.$$

From this,  one obtains the relative redundancy of the code if one assumes,  as here,  that the source itself is redundancy-free:

$$r_c = \frac{R_c - R_q}{R_c}\hspace{0.05cm}.$$

Notes:

• The exercise belongs to the chapter  "Basics of Coded Transmission".

• The transmission code considered here is the second order bipolar code,  but this is not important for the solution of this exercise.

Questions

1

Specify bit duration  $(T_{q})$  and bit rate  $(R_{q})$  of the source.

$T_{q} \ = \ $ $\ \rm µ s $

$R_{q} \ = \ $ $\ \rm Mbit/s $

2

What are the symbol duration  $(T_{c})$  and level number  $(M_{c})$  of the encoder signal?

$T_{c} \ = \ $ $\ \rm µ s $

$M_{c} \ = \ $

3

What is the equivalent bit rate  $R_{c}$  of the encoder signal?

$R_{c} \ = \ $ $\ \rm Mbit/s $

4

Specify the relative redundancy of the code.

$r_{c} \ = \ $ $\ \% $

Solution

Solution

(1)  The bit duration  $T_{q} = \underline{0.5\ \rm µ s}$  can be taken from the graphic.

• Since the source is binary and redundancy-free,  the following applies to the bit rate of the source:

$$R_{q}= 1/T_{q}\ \underline{= 2\ \rm Mbit/s}.$$

(2)  For symbol-wise coding,  $T_{c} = T_{q}$  always applies.

• Thus,  in the present example,  $T_{c}\ \underline{ = 0.5\ \rm µ s}$ is valid.
• The level number  $M_{c}\ \underline{ = 3}$  can be read from the sketch below.

(3)  The symbol rate of the encoder signal is  $2 \cdot 10^{6}$  ternary symbols per second.

• For the equivalent bit rate,  the following applies:

$$R_c = \frac{{\rm log_2} (M_c)}{T_c} = \frac{{\rm log_2}(3)}{0.5\,\,{\rm \mu s}} = \frac{{\rm lg} (3)}{{\rm lg} (2) \cdot 0.5\,\,{\rm \mu s}}= \frac{1.585\,\,{\rm (bit)}}{0.5\,\,{\rm \mu s}}\hspace{0.15cm} \underline {\approx 3.17\,\,{\rm Mbit/s}} \hspace{0.05cm}.$$

(4)  For relative code redundancy,  when the source is redundancy-free,  the general rule is:

$$ r_c = \frac{R_c - R_q}{R_c} = 1- \frac{R_q}{R_c}= 1- \frac{T_c}{T_q \cdot {\rm log_2} (M_c)}\hspace{0.05cm}.$$

• In the case of the second order biploar code considered here,  with parameters  $T_{c} = T_{q}$  and  $M_{c} = 3$,  the following holds:

$$r_c = 1- \frac{1}{{\rm log_2} (3)}\hspace{0.15cm}\underline {\approx 36.9 \% }\hspace{0.05cm}.$$