Exercise 3.11: Viterbi Receiver and Trellis Diagram
The Viterbi receiver allows a low-effort realization of the maximum likelihood decision rule. It contains the system components listed below:
- a matched filter adapted to the basic transmission pulse with frequency response $H_{\rm MF}(f)$ and output signal $m(t)$,
- a sampler spaced at the symbol duration (bit duration) $T$, which converts the continuous-time signal $m(t)$ into the discrete-time sequence $〈m_{\rm \nu}〉$,
- a decorrelation filter with frequency response $H_{\rm DF}(f)$ for removing statistical ties between the noise components of the sequence $〈d_{\rm \nu}〉$,
- the Viterbi decision, which uses a trellis-based algorithm to obtain the sink symbol sequence $〈v_{\rm \nu}〉$.
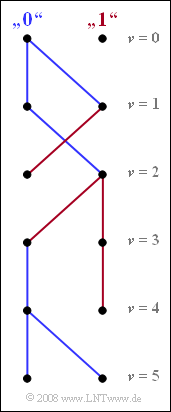
The graph shows the simplified trellis diagram of the two states "$0$" and "$1$" for time points $\nu ≤ 5$. This diagram is obtained as a result of evaluating the two minimum total error quantities ${\it \Gamma}_{\rm \nu}(0)$ and ${\it \Gamma}_{\rm \nu}(1)$ corresponding to "Exercise 3.11Z".
Notes:
- The exercise belongs to the chapter "Viterbi Receiver".
- Reference is also made to the section "MAP and Maximum–Likelihood decision rule".
- All quantities here are to be understood normalized. Also assume unipolar and equal probability amplitude coefficients: ${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$
- The topic is also covered in the interactive applet "Properties of the Viterbi Receiver".
Questions
Musterlösung
- Das Signal $m(t)$ nach dem Matched–Filter $H_{\rm MF}(f)$ weist das größtmögliche Signal–zu–Störleistungsverhältnis auf.
- Die Störanteile der Folge $〈m_{\rm \nu}〉$ sind aber aufgrund der spektralen Formung (stark) korreliert.
- Aufgabe des zeitdiskreten Dekorrelationsfilters mit dem Frequenzgang $H_{\rm DF}(f)$ ist es, diese Bindungen aufzulösen, weshalb für $H_{\rm DF}(f)$ auch der Name "Whitening–Filter" verwendet wird.
- Dies ist allerdings nur auf Kosten einer erhöhten Störleistung möglich ⇒ der letzte Lösungsvorschlag trifft demnach nicht zu.
(2) Die beiden bei $\underline {\nu = 1}$ ankommenden Pfeile sind jeweils blau gezeichnet und kennzeichnen das Symbol $a_1 = 0$. Somit ist bereits zu diesem Zeitpunkt das Ausgangssymbol $a_1$ festgelegt. Ebenso stehen die Symbole $a_3 = 1$ und $a_5 = 0$ bereits zu den Zeitpunkten $\underline {\nu = 3}$ bzw. $\underline {\nu = 5}$ fest.
Dagegen ist zum Zeitpunkt $\nu = 2$ eine Entscheidung bezüglich des Symbols $a_2$ nicht möglich.
- Unter der Hypothese, dass das nachfolgende Symbol $a_3 = 0$ sein wird, würde sich Symbol $a_2 = 1$ ergeben (bei "$0$" kommt ein roter Pfad an, also von "$1$" kommend).
- Dagegen führt die Hypothese $a_3 = 1$ zum Ergebnis $a_2 = 0$ (der bei "$1$" ankommende Pfad ist blau).
Ähnlich verhält es sich zum Zeitpunkt $\nu = 4$.
(3) Aus den durchgehenden Pfaden bei $\nu = 5$ ist ersichtlich:
- $$a_{1}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} a_{2}\hspace{0.15cm}\underline { =0} \hspace{0.05cm},\hspace{0.2cm}a_{3}\hspace{0.15cm}\underline {=1} \hspace{0.05cm},\hspace{0.2cm} a_{4}\hspace{0.15cm}\underline {=0} \hspace{0.05cm},\hspace{0.2cm} a_{5}\hspace{0.15cm}\underline {=0} \hspace{0.05cm}.$$
(4) Richtig ist nur die zweite Aussage:
- Da die Quellensymbole "$0$" und "$1$" als gleichwahrscheinlich vorausgesetzt wurden, ist der ML–Empfänger (Viterbi) identisch mit dem MAP–Empfänger.
- Ein Schwellenwertentscheider (der zu jedem Takt eine symbolweise Entscheidung trifft) hat nur dann die gleiche Fehlerwahrscheinlichkeit wie der Viterbi–Empfänger, wenn es keine Impulsinterferenzen gibt.
- Dies ist hier offensichtlich nicht der Fall, sonst müsste zu jedem Zeitpunkt $\nu$ eine endgültige Entscheidung getroffen werden können.
- Die erste Aussage trifft ebenfalls nicht zu. Das würde nämlich bedeuten, dass der Viterbi–Empfänger bei Vorhandensein von statistischem Rauschen die Fehlerwahrscheinlichkeit $0$ haben kann. Dies ist aus informationstheoretischen Gründen nicht möglich.