Exercise 5.1: Error Distance Distribution
Any digital channel model can be described in the same way by
- the error sequence $〈e_{\rm \nu}〉$, and
- the error distance sequence $〈a_{\rm \nu \hspace{0.05cm}'}〉$.
As an example, we consider the sequences:
- $$<\hspace{-0.1cm}e_{\nu} \hspace{-0.1cm}> \ = \ < \hspace{-0.1cm}0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, \text{...} \hspace{-0.1cm}> \hspace{0.05cm},$$
- $$< \hspace{-0.1cm}a_{\nu\hspace{0.05cm} '} \hspace{-0.15cm}> \ = \ <\hspace{-0.1cm}2, 3, 1, 4, 2, 5, 1, 1, 3, 4, 1, 2, \text{...} \hspace{-0.1cm}> \hspace{0.05cm}.$$
One can see from this, for example:
- The error distance $a_2 = 3$ means that there are two error-free symbols between the first and the second error.
- In contrast, $a_3 = 1$ indicates that the second error is immediately followed by a third.
The different indices $(\nu$ and $\nu\hspace{0.05cm} '$, each starting with $1$) are necessary because there is no synchrony between the error distance sequence and the error sequence.
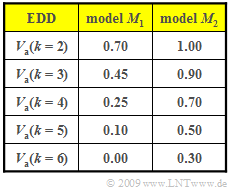
In the graph, for two different models $M_1$ and $M_2$, the "error distance distribution" $\rm (EDD)$ is given as
- $$V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}$$
This table is to be evaluated in this exercise.
Note: The exercise belongs to the chapter "Parameters of Digital Channel Models".
Questions
Solution
- It follows: $e_{\rm 16} \ \underline {= 0}$, $e_{\rm 17} \ \underline {= 1}$, $e_{\rm 18} \ \underline {= 1}$.
(2) From the definition equation follows already
- $$V_a(k = 1) = {\rm Pr}(a \ge 1)\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$
(3) ${\rm Pr}(a = k) = V_a(k) \, –V_a(k+1)$ holds. From this we obtain for the individual probabilities:
- $${\rm Pr}(a = 1)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(1) - V_a(2) = 1 - 0.7\hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$
- $${\rm Pr}(a = 2)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(2) - V_a(3) = 0.7 - 0.45 \hspace{0.15cm}\underline {= 0.25}\hspace{0.05cm},$$
- $${\rm Pr}(a = 3)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(3) - V_a(4) = 0.45 - 0.25 \hspace{0.15cm}\underline {= 0.2}\hspace{0.05cm},$$
- $${\rm Pr}(a = 4)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(4) - V_a(5) = 0.25 - 0.10 \hspace{0.15cm}\underline {= 0.15}\hspace{0.05cm},$$
- $${\rm Pr}(a = 5)\hspace{-0.1cm} \ = \ \hspace{-0.1cm}V_a(5) - V_a(6) = 0.10 - 0 \hspace{0.15cm}\underline {= 0.10}\hspace{0.05cm}.$$
(4) From $V_a(k=6) = {\rm Pr}(a ≥ 6) = 0$, it follows directly for the maximum error distance
- $$k_{\rm max} \ \underline {= 5}.$$
(5) Using the probabilities calculated in subtask (3), the expected value we are looking for is:
- $${\rm E}\big[a \big] = \sum_{k = 1}^{5} k \cdot {\rm Pr}(a = k) = 1 \cdot 0.3 +2 \cdot 0.25 +3 \cdot 0.2 +4 \cdot 0.15 +5 \cdot 0.1\hspace{0.15cm}\underline { = 2.5} \hspace{0.05cm}.$$
(6) The mean error probability is the inverse of the average error distance:
- $$p_{\rm M} \ \underline {= 0.4}.$$
(7) With certainty, only statement 1 is true:
- The first statement is true because ${\rm Pr}(a = 1) = V_a(1) - V_a(2) = 0$.
- The second statement is not certain because $V_a(6)$ gives only the sum of the probabilities ${\rm Pr}(a ≥ 6)$, but not ${\rm Pr}(a = 6)$ alone.
- Only with the additional specification $V_a(7) = 0$ would statement 2 be true.
- Likewise, for the expected value ${\rm E}[a]$, no definite statement is possible due to missing information. With $V_a(7) = 0$ the result would be:
- $${\rm E}[a] = 2 \cdot 0.1 +3 \cdot 0.2 +4 \cdot 0.2 +5 \cdot 0.2 +6 \cdot 0.3= 4.4.$$
- Without this specification, only the statement ${\rm E}[a] ≥ 4.4$ is possible. But this means that the condition $p_{\rm M} < 1/4.4 < 0.227$ is valid for the mean error probability. The statement 3 is therefore also not true with certainty.