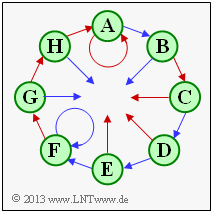
Exercise 3.6Z: Transition Diagram at 3 States
In the state transition diagram of an encoder with memory $m$ there are $2^m$ states. Therefore, the diagram shown with eight states describes a convolutional encoder with memory $m = 3$.
Usually the states are denoted by $S_0, \ \text{...} \ , \ S_{\mu}, \ \text{...} \ , \ S_7$, where the index $\mu$ is determined from the occupancy of the shift register (contents from left to right: $u_{i-1}, u_{i-2}, u_{i-3})$ :
- $$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2\hspace{0.03cm}^{l-1} \cdot u_{i-l} \hspace{0.05cm}.$$
The state $S_0$ therefore results for the shift register content "$000$", the state $S_1$ for "$100$" and the state $S_7$ for "$111$".
However, in the above graphic, for the states $S_0, \, \text{...} \, , \, S_7$ placeholder names $\mathbf{A}, \, \text{...} \, , \, \mathbf{H}$ used. In the subtasks (1) and (2) you should clarify which placeholder stands for which state.
For convolutional encoders of rate $1/n$, which will be exclusively considered here, two arrows depart from each state $S_{\mu}$ ,
- one red one for the current information bit $u_i = 0$ and.
- a blue one for $u_i = 1$.
This is another reason why the state transition diagram shown is not complete. It is to be mentioned furthermore:
- At each state also two arrows arrive, whereby these can be absolutely of the same color.
- Next to the arrows there are usually the $n$ code bits. This was also omitted here.
Hints:
- The exercise belongs to the chapter "Code Description with State and Trellis Diagram".
- In "Exercise 3.7Z" two convolutional codes with memory $m = 3$ are examined, both of which can be described by the transition diagram analyzed here.
- Please include the appropriate index $\mu$ for all questions.
- Reference is made in particular to the sections
Questions
Solution
(1) The placeholder $\mathbf{A}$ represents the state $S_0$ ⇒ $u_{i-1} = 0, \ u_{i-2} = 0, \ u_{i-3} = 0$.
- This is the only state $S_{\mu}$ where one remains in the same state $S_{\mu}$ by the infobit $u_i = 0$ (red arrow).
- From the state $S_7$ ⇒ $u_{i-1} = 1, \ u_{i-2} = 1, \ u_{i-3} = 1$ one comes with $u_i = 1$ (blue arrow) also again to the state $S_7$.
- Thus, for $\mathbf{A}$ the index $\underline{\mu = 0}$ and for $\mathbf{F}$ the index $\underline{\mu = 7}$ had to be entered.
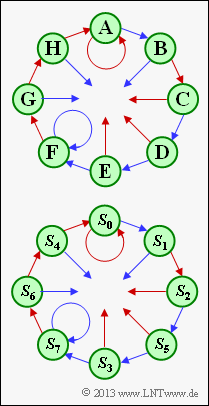
(2) Starting from the state $\mathbf{A} = S_0$, one arrives at the following states according to the initial graph in a clockwise direction with the red arrows $(u_i = 0)$ or the blue arrows $(u_i = 1)$:
- $$u_{i–3} = 0, \ u_{i–2} = 0, \ u_{i–1} = 0, \ u_i = 1 ⇒ s_{i+1} = \mathbf{B} = S_1,$$
- $$u_{i–3} = 0, \ u_{i–2} = 0, \ u_{i–1} = 1, \ u_i = 0 ⇒ s_{i+1} = \mathbf{C} = S_2,$$
- $$u_{i–3} = 0, \ u_{i–2} = 1, \ u_{i–1} = 0, \ u_i = 1 ⇒ s_{i+1} = \mathbf{D} = S_5,$$
- $$u_{i–3} = 1, \ u_{i–2} = 0, \ u_{i–1} = 1, \ u_i = 1 ⇒ s_{i+1} = \mathbf{E} = S_3,$$
- $$u_{i–3} = 0, \ u_{i–2} = 1, \ u_{i–1} = 1, \ u_i = 1 ⇒ s_{i+1} = \mathbf{F} = S_7,$$
- $$u_{i–3} = 1, \ u_{i–2} = 1, \ u_{i–1} = 1, \ u_i = 0 ⇒ s_{i+1} = \mathbf{G} = S_6,$$
- $$u_{i–3} = 1, \ u_{i–2} = 1, \ u_{i–1} = 0, \ u_i = 0 ⇒ s_{i+1} = \mathbf{H} = S_4,$$
- $$u_{i–3} = 1, \ u_{i–2} = 0, \ u_{i–1} = 0, \ u_i = 0 ⇒ s_{i+1} = \mathbf{A} = S_0.$$
- So the indices $\mu$ are to be entered in the order 1, 2, 5, 3, 6, 4.
- The graphic shows the connection between the placeholders and the states $S_{\mu}$.
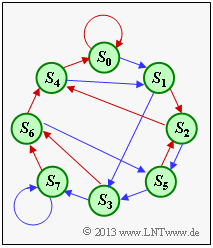
(3) From state $S_1$ ⇒ $u_{i–1} = 1, \ u_{i–2} = 0, \ u_{i–3} = 0$ one arrives with $u_i = 0$ (red arrow) at state $S_2$. On the other hand, with $u_i = 1$ (blue arrow) one ends up at the state $S_3$ ⇒ $u_{i–1} = 1, \ u_{i–2} = 1, \ u_{i–3} = 0$.
The adjacent graphic shows the state transition diagram with all transitions. From this it can be read:
- From state $S_3$ one comes with $u_i = 0$ to state $S_6$.
- From the state $S_5$ one comes with $u_i = 0$ to the state $S_2$.
- From the state $S_7$ one comes with $u_i = 0$ to the state $S_6$.
Thus, the indices are to be entered in the order 3, 6, 2, 6.