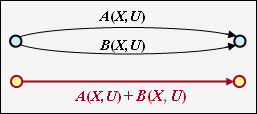Distance Characteristics and Error Probability Bounds

1. Channel Coding
2. Convolutional Codes and Their Decoding
3. Distance Characteristics and Error Probability Bounds

• Previous page
• Next page

• Previous page
• Next page

Free distance vs. minimum distance

An important parameter regarding the error probability of linear block codes is the  minimum distance  between two code words  $\underline{x}$  and  $\underline{x}\hspace{0.05cm}'$:

\[d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]

The second part of the equation arises from the fact that every linear code also includes the zero word  $(\underline{0})$ . It is therefore convenient to set  $\underline{x}\hspace{0.05cm}' = \underline{0}$, so that the  "Hamming distance"  $d_{\rm H}(\underline{x}, \ \underline{0})$  gives the same result as Hamming weight  $w_{\rm H}(\underline{x})$.

Code word of the  $(7, 4, 3)$ Hamming code

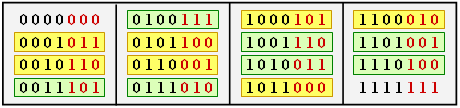
$\text{Example 1:}$  The table shows the 16 codewords of the  "$(7, 4, 3)$–Hamming codes" 
$($see  $\text{Example 7})$.

• All codewords except the null word  $(\underline{0})$  contain at least three ones   ⇒   $d_{\rm min} = 3$.
• There are seven codewords with three ones (highlighted in yellow), seven with four ones (highlighted in green), and one each with no ones and seven ones

.

The  free distance  $d_{\rm F}$  of a (convolutional code   ⇒   $\mathcal{CC}$) is formulaically no different from the minimum distance of a linear block code:

\[d_{\rm F}(\mathcal{CC}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}\hspace{0.05cm}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}\hspace{0.05cm}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}\hspace{0.05cm}') = \min_{\substack{\underline{x} \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{CC} \\ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{0}}}\hspace{0.1cm}w_{\rm H}(\underline{x}) \hspace{0.05cm}.\]

In the literature instead of  $d_{\rm F}$  sometimes also  $d_{∞}$  is used.

• Major difference to minimal distance is that in convolutional codes not information– and codewords are to be considered, but sequences with the property  "semi–infinite".
  

• Each code sequence  $\underline{x}$  describes a path through the trellis.
• The free distance is the smallest possible Hamming weight of such a path (except for the zero path).
  

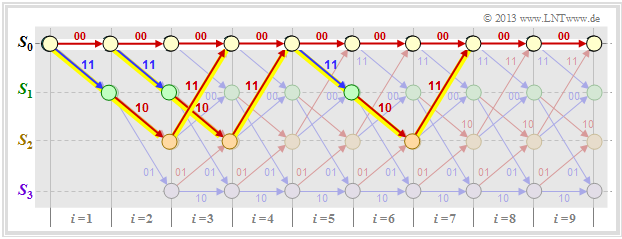
The graph shows three of the infinite paths with the minimum Hamming weight  $w_{\rm H, \ min}(\underline{x}) = d_{\rm F} = 5$.

Einige Pfade mit  $w(\underline{x}) = d_{\rm F} = 5$

Path weighting enumerator function

For any linear block code, a weight enumerator function can be given in a simple way because of the finite number of codewords  $\underline{x}$ . For the  $\text{"Example 1"}$  on the previous page this is:

\[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.\]

In the case of a (non terminated) convolutional code, no such weight function can be given, since there are infinitely many, infinitely long code sequences  $\underline{x}$  and thus also infinitely many trellis paths. To get a grip on this problem, we now assume the following:

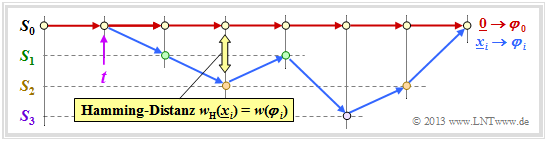
• As a reference for the trellis diagram, we always choose the path of the code sequence  $\underline{x} = \underline{0}$  and call this the zero path  $\varphi_0$.
  

• We now consider only those paths  $\varphi_j ∈ {\it \Phi}$ that all deviate from the zero path at a given time  $t$  and return to it at some point.
  
  

Although only a fraction of all paths belong to the set  ${\it \Phi}$  , ${\it \Phi} = \{\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} \}$  still an unbounded set of paths. $\varphi_0$  is not one of them.

Some paths and their path weightings

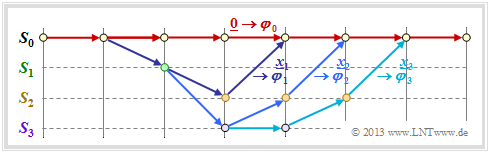
In the above trellis some paths  $\varphi_j ∈ {\it \Phi}$  are drawn:

• The yellow path  $\varphi_1$  belongs to the sequence  $\underline{x}_1 = (11, 10, 11)$  with hamming–weight  $w_{\rm H}(\underline{x}_1) = 5$. Thus, the path weighting  $w(\varphi_1) = 5$ as well. Due to the definition of the branching time  $t$  only this single path  $\varphi_1$  has the free distance  $d_{\rm F} = 5$  to the zero path   ⇒   $A_5 = 1$.
  

• For the two green paths with corresponding sequences  $\underline{x}_2 = (11, 01, 01, 11)$  and   $\underline{x}_3 = (11, 10, 00, 10, 11)$  respectively,  $w(\varphi_2) = w(\varphi_3) = 6$ holds. No other path exhibits the path weighting  $6$ . We take this fact into account by the coefficient  $A_6 = 2$.
  

• Also drawn is the gray path  $\varphi_4$, associated with the sequence  $\underline{x}_4 = (11, 01, 10, 01, 11)$   ⇒   $w(\varphi_4) = 7$. Also, the sequences  $\underline{x}_5 = (11, 01, 01, 00, 10, 11)$,  $\underline{x}_6 = (11, 10, 00, 01, 01, 11)$  and  $\underline{x}_7 = (11, 10, 00, 10, 00, 10, 11)$  have path weighting  $7$    ⇒   $A_7 = 4$.
  
  

Thus, the path weighting enumerator function is:

\[T(X) = A_5 \cdot X^5 + A_6 \cdot X^6 + A_7 \cdot X^7 + \text{...} \hspace{0.1cm}= X^5 + 2 \cdot X^6 + 4 \cdot X^7+ \text{...}\hspace{0.1cm} \hspace{0.05cm}.\]

The definition of this function  $T(X)$  is:

$\text{Definition:}$  For the  path weighting enumerator function  of a convolutional code holds:

\[T(X) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j) } \hspace{0.1cm}=\hspace{0.1cm} \sum_{w\hspace{0.05cm} =\hspace{0.05cm} d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w \hspace{0.05cm}.\]

• ${\it \Phi}$  denotes the set of all paths that leave the zero path  $\varphi_0$  exactly at the specified time  $t$  and return to it (sometime) later.
  

• According to the second part of the equation, the summands are ordered by their path weightings  $w$  where  $A_w$  denotes the number of paths with path weighting  $w$ .
• The sum starts with  $w = d_{\rm F}$.
  

• The path weighting  $w(\varphi_j)$  is equal to the Hamming weight (number of ones) of the code sequence associated to the path  $\varphi_j$  $\underline{x}_j$:

\[w({\varphi_j) = w_{\rm H}(\underline {x} }_j) \hspace{0.05cm}.\]

Note:   The weight enumerator function  $W(X)$  defined for linear block codes and the path weight function  $T(X)$  of convolutional codes have many similarities; however, they are not identical.

We consider again the weight enumerator function of the  $(7, 4, 3)$–Hamming code,

\[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7},\]

and the path weighting enumerator function of our standard–convolutional coder,

\[T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7+ 8 \cdot X^8+ \text{...} \]

Noticeable is the "$1$" in the first equation, which is missing in the second equation. That is:   For the linear block codes, the reference–codeword  $\underline{x}_i = \underline{0}$  is counted, whereas the zero code sequence  $\underline{x}_i = \underline{0}$  or the zero path  $\varphi_0$  is excluded by definition for the convolutional codes.

$\text{Author's personal opinion:}$ 

One could  have defined $W(X)$  without the "$1$" as well. This would have avoided, among other things, that the Bhattacharyya–bound for linear block codes and that for convolutional codes differ by "$-1$", as can be seen from the following equations:

• "Bhattacharyya bound for linear block codes":     ${\rm Pr(Block\:error)} \le W(X = \beta) -1 \hspace{0.05cm},$

• "Bhattacharyya bound for convolutional codes":     ${\rm Pr(Burst\:error)} \le T(X = \beta) \hspace{0.05cm}.$

Enhanced path weighting enumerator function

The path weighting enumerator function  $T(X)$  only provides information regarding the weights of the code sequence  $\underline{x}$.

• More information is obtained if the weights of the information sequence  $\underline{u}$  are also collected.
• One then needs two formal parameters  $X$  and  $U$, as can be seen from the following definition.
  

$\text{Definition:}$  The  enhanced path weight enumerator function (EPWEF)  is:

\[T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi} }\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{ { u}(\varphi_j)} \hspace{0.1cm}=\hspace{0.1cm} \sum_{w} \sum_{u}\hspace{0.1cm} A_{w, \hspace{0.05cm}u} \cdot X^w \cdot U^{u} \hspace{0.05cm}.\]

All specifications for  $T(X)$–definition on the last page apply. In addition, note:

• The path input weight  $u(\varphi_j)$  is equal to the Hamming weight of the information sequence associated to the path  $\varphi_j$  $\underline{u}_j$. It is expressed as a power of the formal parameter  $U$ .
  

• The coefficient  $A_{w, \ u}$  denotes the number of paths  $\varphi_j$  with path output weight  $w(\varphi_j)$  and path input weight  $u(\varphi_j)$. The run variable for the second portion is  $u$ .
  

• Setting the formal parameter  $U = 1$ in the enhanced path weighting enumerator function yields the original weighting enumerator function  $T(X)$  according to the definition on the last page.
  

For many (and all relevant) convolutional codes, upper equation can still be simplified:

\[T_{\rm enh}(X, U) =\hspace{0.1cm} \sum_{w \ = \ d_{\rm F} }^{\infty}\hspace{0.1cm} A_w \cdot X^w \cdot U^{u} \hspace{0.05cm}.\]

$\text{Example 2:}$  Thus, the enhanced path weighting enumerator function of our standard coder is:

\[T_{\rm enh}(X, U) = U \cdot X^5 + 2 \cdot U^2 \cdot X^6 + 4 \cdot U^3 \cdot X^7+ \text{ ...} \hspace{0.1cm} \hspace{0.05cm}.\]

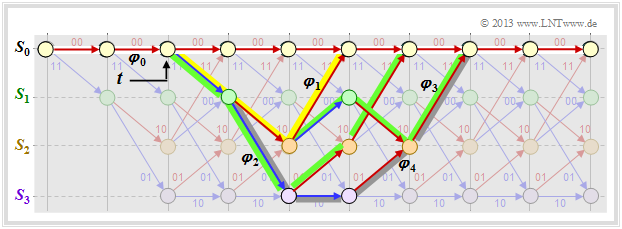
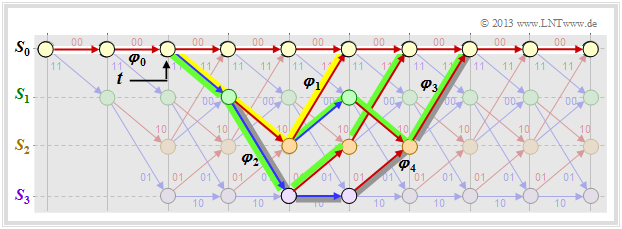
If we compare this result with the trellis shown below, we can see:

• The yellow highlighted path – marked by  $X^5$  – is composed of a blue arrow  $(u_i = 1)$  and two red arrows  $(u_i = 0)$ . Thus  $X^5$  becomes the extended term  $UX^5$.
  

• The sequences of the two green paths are  $\underline{u}_2 = (1, 1, 0, 0)$   ⇒   $\underline{x}_2 = (11, 01, 01, 11)$  and  $\underline{u}_3 = (1, 0, 1, 0, 0)$   ⇒   $\underline{x}_3 = (11, 10, 00, 10, 11)$. This gives the second term  $2 \cdot U^2X^6$.
  

• The gray path (and the three undrawn paths) together make the contribution  $4 \cdot U^3X^7$. Each of these paths contains three blue arrows   ⇒   three ones in the associated information sequence.
  

Some paths and their path weightings

Path weighting enumerator function from state transition diagram

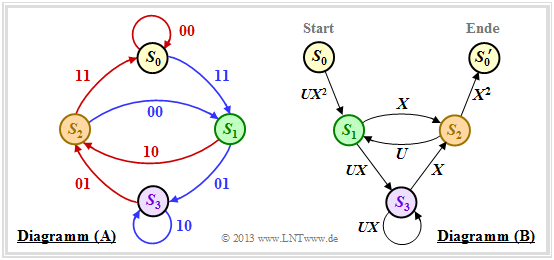
Es gibt eine elegante Methode, um die Pfadgewichtsfunktion  $T(X)$  und deren Erweiterung direkt aus dem Zustandsübergangsdiagramm zu bestimmen. Dies soll hier und auf den folgenden Seiten am Beispiel unseres  Standardcodierers  demonstriert werden.

Zunächst muss dazu das Zustandsübergangsdiagramm umgezeichnet werden. Die Grafik zeigt dieses links in der bisherigen Form als Diagramm  $\rm (A)$, während rechts das neue Diagramm  $\rm (B)$  angegeben ist.

Zustandsübergangsdiagramm in zwei verschiedenen Varianten

Man erkennt:

• Der Zustand  $S_0$  wird aufgespalten in den Startzustand  $S_0$  und den Endzustand  $S_0\hspace{0.01cm}'$. Damit lassen sich alle Pfade des Trellisdiagramms, die im Zustand  $S_0$  beginnen und irgendwann zu diesem zurückkehren, auch im rechten Graphen  $\rm (B)$  nachvollziehen. Ausgeschlossen sind dagegen direkte Übergänge von  $S_0$  nach  $S_0\hspace{0.01cm}'$  und damit auch der Nullpfad  $($Dauer–$S_0)$.
  

• Im Diagramm  $\rm (A)$  sind die Übergänge anhand der Farben Rot  $($für  $u_i = 0)$  und Blau  $($für  $u_i = 1)$  unterscheidbar, und die Codeworte  $\underline{x}_i ∈ \{00, 01, 10, 11\}$  sind an den Übergängen vermerkt. Im neuen Diagramm  $\rm (B)$  werden  $(00)$  durch  $X^0 = 1$  und  $(11)$  durch  $X^2$  ausgedrückt. Die Codeworte  $(01)$  und  $(10)$  sind nun nicht mehr unterscheidbar, sondern werden einheitlich mit  $X$  bezeichnet.
  

• Anders formuliert:   Das Codewort  $\underline{x}_i$  wird nun als  $X^w$  dargestellt, wobei  $X$  eine dem Ausgang (der Codesequenz) zugeordnete Dummy–Variable ist und  $w = w_{\rm H}(\underline{x}_i)$  das Hamming–Gewicht des Codewortes  $\underline{x}_i$  angibt. Bei einem Rate–$1/2$–Code ist der Exponent  $w$  entweder  $0, \ 1$  oder  $2$.
  

• Ebenfalls verzichtet wird im Diagramm  $\rm (B)$  auf die Farbcodierung. Das Informationsbit  $u_i = 1$  wird nun durch  $U^1 = U$  und das Informationsbit  $u_i = 0$  durch  $U^0 = 1$  gekennzeichnet. Die Dummy–Variable  $U$  ist also der Eingangssequenz  $\underline{u}$  zugeordnet.
  
  

Regeln zur Manipulation des Zustandsübergangsdiagramms

Ziel unserer Berechnungen wird es sein, den (beliebig komplizierten) Weg von  $S_0$  nach  $S_0\hspace{0.01cm}'$  durch die erweiterte Pfadgewichtsfunktion  $T_{\rm enh}(X, \ U)$  zu charakterisieren. Dazu benötigen wir Regeln, um den Graphen schrittweise vereinfachen zu können.

Erfassung serieller Übergänge

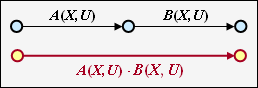
Serielle Übergänge

Zwei serielle Verbindungen – gekennzeichnet durch  $A(X, \ U)$  und  $B(X, \ U)$  – können durch eine einzige Verbindung mit dem Produkt dieser Bewertungen ersetzt werden.

Erfassung paralleler Übergänge

Parallele Übergänge

Zwei parallele Verbindungen – gekennzeichnet durch  $A(X, \ U)$  und  $B(X, \ U)$  – werden durch die Summe ihrer Bewertungsfunktionen zusammengefasst.

Reduzierung eines Rings

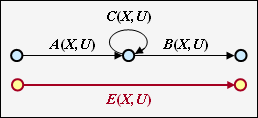
Ring

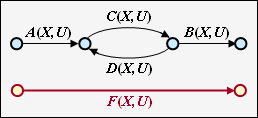
Die nebenstehende Konstellation kann durch eine einzige Verbindung ersetzt werden, wobei für die Ersetzung gilt:

\[E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} \hspace{0.05cm}.\]

Reduzierung einer Rückkopplung

Rückkopplung

Durch die Rückkopplung können sich hier zwei Zustände beliebig oft abwechseln. Für diese Konstellation gilt:

\[F(X, U) = \frac{A(X, U) \cdot B(X, U)\cdot C(X, U)}{1- C(X, U)\cdot D(X, U)} \hspace{0.05cm}.\]

Die hier angegebenen Gleichungen für Ring und Rückkopplung sind in der  Aufgabe 3.12Z  zu beweisen.

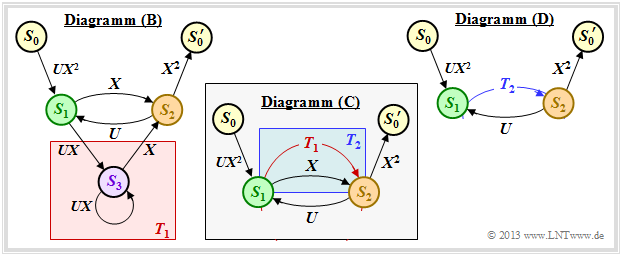
$\text{Beispiel 3:}$  Die oben genannten Regeln sollen nun auf unser Standardbeispiel angewendet werden. In der Grafik sehen Sie links das modifizierte Diagramm  $\rm (B)$.

Zur Reduktion der Zustandsübergänge

• Zunächst ersetzen wir den rot hinterlegten Umweg von  $S_1$  nach  $S_2$  über  $S_3$  im Diagramm  $\rm (B)$  durch die im Diagramm  $\rm (C)$  eingezeichnete rote Verbindung  $T_1(X, \hspace{0.05cm} U)$. Es handelt sich nach der oberen Klassifizierung um einen "Ring" mit den Beschriftungen  $A = C = U \cdot X$  und  $B = X$, und wir erhalten für die erste Reduktionsfunktion:

\[T_1(X, \hspace{0.05cm} U) = \frac{U \cdot X^2}{1- U \cdot X} \hspace{0.05cm}.\]

• Nun fassen wir die parallelen Verbindungen entsprechend der blauen Hinterlegung im Diagramm  $\rm (C)$  zusammen und ersetzen diese durch die blaue Verbindung im Diagramm  $\rm (D)$. Die zweite Reduktionsfunktion lautet somit:

\[T_2(X, \hspace{0.05cm}U) = T_1(X, \hspace{0.05cm}U) + X = \frac{U X^2 + X \cdot (1-UX)}{1- U X} = \frac{X}{1- U X} \hspace{0.05cm}.\]

• Der gesamte Graph  $\rm (D)$  kann dann durch eine einzige Verbindung von  $S_0$  nach  $S_0\hspace{0.01cm}'$  ersetzt werden. Nach der Rückkopplungsregel erhält man für die  erweiterte Pfadgewichtsfunktion:

\[T_{\rm enh}(X, \hspace{0.05cm}U) = \frac{(U X^2) \cdot X^2 \cdot \frac{X}{1- U X} }{1- U \cdot \frac{X}{1- U X} } = \frac{U X^5}{1- U X- U X} = \frac{U X^5}{1- 2 \cdot U X} \hspace{0.05cm}.\]

• Mit der Reihenentwicklung  $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \ $  lässt sich hierfür auch schreiben:

\[T_{\rm enh}(X, \hspace{0.05cm}U) = U X^5 \cdot \big [ 1 + 2 \hspace{0.05cm}UX + (2 \hspace{0.05cm}UX)^2 + (2 \hspace{0.05cm}UX)^3 + \text{...} \hspace{0.05cm} \big ] \hspace{0.05cm}.\]

• Setzt man die formale Input–Variable  $U = 1$, so erhält man die "einfache" Pfadgewichtsfunktion, die allein Aussagen über die Gewichtsverteilung der Ausgangssequenz  $\underline{x}$  erlaubt:

\[T(X) = X^5 \cdot \big [ 1 + 2 X + 4 X^2 + 8 X^3 +\text{...}\hspace{0.05cm} \big ] \hspace{0.05cm}.\]

Das gleiche Ergebnis haben wir bereits aus dem Trellisdiagramm auf der Seite  Pfadgewichtsfunktion  abgelesen. Dort gab es einen grauen Pfad mit Gewicht  $5$, zwei gelbe Pfade mit Gewicht  $6$  und vier grüne Pfade mit Gewicht  $7$.

Blockfehlerwahrscheinlichkeit vs. Burstfehlerwahrscheinlichkeit

Einfaches Übertragungsmodell inklusive Codierung/Decodierung

Das einfache Modell gemäß der Skizze gilt sowohl für lineare Blockcodes als auch für Faltungscodes.

Blockcodes

Bei den Blockcodes bezeichnen  $\underline{u} = (u_1, \ \text{...} \hspace{0.05cm}, \ u_i, \ \text{...} \hspace{0.05cm}, \ u_k)$  und  $\underline{v} = (v_1, \ \text{...} \hspace{0.05cm}, v_i, \ \text{...} \hspace{0.05cm} \ , \ v_k)$  die Informationsblöcke am Eingang und Ausgang des Systems.

Damit sind folgende Beschreibungsgrößen angebbar:

• die Blockfehlerwahrscheinlichkeit   ${\rm Pr(Blockfehler)} = {\rm Pr}(\underline{v} ≠ \underline{u}),$

• die Bitfehlerwahrscheinlichkeit   ${\rm Pr(Bitfehler)} = {\rm Pr}(v_i ≠ u_i).$
  
  

$\text{Bitte beachten Sie:}$  Bei realen Übertragungssystemen gilt aufgrund des thermischen Rauschens stets:

$${\rm Pr(Bitfehler)} > 0\hspace{0.05cm},\hspace{1.0cm}{\rm Pr(Blockfehler)} > {\rm Pr(Bitfehler)} \hspace{0.05cm}.$$

Hierfür ein einfacher Erklärungsversuch:   Entscheidet der Decoder in jedem Block der Länge  $k$  genau ein Bit falsch,

• so beträgt auch die mittlere Bitfehlerwahrscheinlichkeit  ${\rm Pr(Bitfehler)}= 1/k$,
• während für die Blockfehlerwahrscheinlichkeit  ${\rm Pr(Blockfehler)}\equiv 1$  gilt.

Faltungscodes

Bei Faltungscodes ist die Blockfehlerwahrscheinlichkeit nicht angebbar, da hier  $\underline{u} = (u_1, \ u_2, \ \text{...} \hspace{0.05cm})$  und  $\underline{\upsilon} = (v_1, \ v_2, \ \text{...} \hspace{0.05cm})$  Sequenzen darstellen.

Selbst der kleinstmögliche Codeparameter  $k = 1$  führt hier zur Sequenzlänge  $k \hspace{0.05cm}' → ∞$, und die Blockfehlerwahrscheinlichkeit ergäbe sich stets zu  ${\rm Pr(Blockfehler)}\equiv 1$, selbst wenn die Bitfehlerwahrscheinlichkeit extrem klein (aber ungleich Null) ist.

Nullpfad  ${\it \varphi}_0$  und Abweichungspfade  ${\it \varphi}_i$

$\text{Definition:}$  Für die  Burstfehlerwahrscheinlichkeit  eines Faltungscodes gilt:

\[{\rm Pr(Burstfehler)} = {\rm Pr}\big \{ {\rm Decoder\hspace{0.15cm} verl\ddot{a}sst\hspace{0.15cm} zur\hspace{0.15cm} Zeit}\hspace{0.15cm}t \hspace{0.15cm}{\rm den \hspace{0.15cm}korrekten \hspace{0.15cm}Pfad}\big \} \hspace{0.05cm}.\]

• Um für die folgende Herleitung die Schreibweise zu vereinfachen, gehen wir stets von der Nullsequenz  $(\underline{0})$  aus, die im gezeichneten Trellis als Nullpfad  $\varphi_0$  rot dargestellt ist.
• Alle anderen Pfade  $\varphi_1, \ \varphi_2, \ \varphi_3, \ \text{...} $  (und noch viele mehr) verlassen  $\varphi_0$  zur Zeit  $t$. Sie alle gehören zur Pfadmenge  ${\it \Phi}$   ⇒   "Viterbi–Decoder verlässt den korrekten Pfad zur Zeit  $t$". Diese Wahrscheinlichkeit wird auf der nächsten Seite berechnet.

Burst error probability and Bhattacharyya bound

Wir gehen wie im früheren Kapitel  Schranken für die Blockfehlerwahrscheinlichkeit  von der paarweisen Fehlerwahrscheinlichkeit  ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$  aus, dass der Decoder anstelle des Pfades  $\varphi_0$  den Pfad  $\varphi_i$  auswählen könnte. Alle betrachteten Pfade  $\varphi_i$  verlassen den Nullpfad  $\varphi_0$  zum Zeitpunkt  $t$; sie gehören somit alle zur Pfadmenge  ${\it \Phi}$.

Zur Berechnung der Burstfehlerwahrscheinlichkeit

Die gesuchte  Burstfehlerwahrscheinlichkeit  ist gleich der folgenden Vereinigungsmenge:

\[{\rm Pr(Burstfehler)}= {\rm Pr}\left (\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}1}\big] \hspace{0.05cm}\cup\hspace{0.05cm}\big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}2}\big]\hspace{0.05cm}\cup\hspace{0.05cm} \text{... }\hspace{0.05cm} \right )= {\rm Pr} \left ( \cup_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}} \hspace{0.15cm} \big[\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big] \right )\hspace{0.05cm}.\]

Eine obere Schranke hierfür bietet die so genannte  Union–Bound:

\[{\rm Pr(Burstfehler)} \le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} {\rm Pr}\big [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\big ] = {\rm Pr(Union \hspace{0.15cm}Bound)} \hspace{0.05cm}.\]

Die paarweise Fehlerwahrscheinlichkeit kann mit der  Bhattacharyya–Schranke  abgeschätzt werden:

\[{\rm Pr}\big [\underline {0} \mapsto \underline {x}_{\hspace{0.02cm}i}\big ] \le \beta^{w_{\rm H}({x}_{\hspace{0.02cm}i})}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm Pr}\left [\varphi_{\hspace{0.02cm}0} \mapsto \varphi_{\hspace{0.02cm}i}\right ] \le \hspace{0.05cm} \beta^{w(\varphi_i)}\hspace{0.05cm}.\]

Hierbei bezeichnet

• $w_{\rm H}(\underline{x}_i)$  das Hamming–Gewicht der möglichen Codesequenz  $\underline{x}_i,$
• $\ w(\varphi_i)$  das Pfadgewicht des entsprechenden Pfades  $\varphi_i ∈ {\it \Phi}$, und
• $\beta$  den so genannten  Bhattacharyya–Kanalparameter.
  

Durch Summation über alle Pfade und einen Vergleich mit der (einfachen)  Pfadgewichtsfunktion  $T(X)$  erhalten wir das Ergebnis:

\[{\rm Pr(Burstfehler)} \le T(X = \beta),\hspace{0.5cm}{\rm mit}\hspace{0.5cm} T(X) = \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.15cm} \hspace{0.05cm} X^{w(\varphi_i)}\hspace{0.05cm}.\]

$\text{Beispiel 4:}$  Für unseren Standardcodierer   ⇒   $R = 1/2, \ \ m = 2, \ \ \mathbf{G}(D) = (1 + D + D^2, \ 1 + D)$  haben wir folgende  Pfadgewichtsfunktion  erhalten:

\[T(X) = X^5 + 2 \cdot X^6 + 4 \cdot X^7 + \ \text{...} \hspace{0.1cm} = X^5 \cdot ( 1 + 2 \cdot X + 4 \cdot X^2+ \ \text{...} \hspace{0.1cm}) \hspace{0.05cm}.\]

Mit der Reihenentwicklung  $1/(1 \, –x) = 1 + x + x^2 + x^3 + \ \text{...} \hspace{0.15cm} $  kann hierfür auch geschrieben werden:

\[T(X) = \frac{X^5}{1-2 \cdot X} \hspace{0.05cm}.\]

Das BSC–Modell liefert mit der Verfälschungswahrscheinlichkeit  $\varepsilon$  folgende Bhattacharyya–Schranke:

\[{\rm Pr(Burstfehler)} \le T(X = \beta) = T\big ( X = 2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)} \big ) = \frac{(2 \cdot \sqrt{\varepsilon \cdot (1-\varepsilon)})^5}{1- 4\cdot \sqrt{\varepsilon \cdot (1-\varepsilon)}}\hspace{0.05cm}.\]

In der  Aufgabe 3.14  soll diese Gleichung numerisch ausgewertet werden.

Bitfehlerwahrscheinlichkeit und Viterbi–Schranke

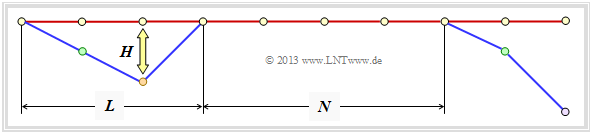
Abschließend wird eine obere Schranke für die Bitfehlerwahrscheinlichkeit angegeben. Gemäß der Grafik gehen wir wie in  [Liv10]  von folgenden Gegebenheiten aus:

• Gesendet wurde die Nullsequenz  $\underline{x} = \underline{0}$   ⇒   Pfad  $\varphi_0$.
  

• Die Dauer einer Pfadabweichung (englisch:   Error Burst Duration ) wird mit  $L$  bezeichnet.
  

• Den Abstand zweier Bursts (englisch:   Inter–Burst Time ) nennen wir  $N$.
  

• Das Hamming–Gewicht des Fehlerbündels sei  $H$.
  

Zur Definition der Beschreibungsgrößen  $L$,  $N$  und $H$

Für einen Rate–$1/n$–Faltungscode   ⇒   $k = 1$, also einem Informationsbit pro Takt, lässt sich aus den Erwartungswerten  ${\rm E}\big[L \big]$, ${\rm E}\big[N \big]$  und  ${\rm E}\big[H\big]$  der oben definierten Zufallsgrößen eine obere Schranke für die Bitfehlerwahrscheinlichkeit angeben:

\[{\rm Pr(Bitfehler)} = \frac{{\rm E}\big[H\big]}{{\rm E}[L] + {\rm E}\big[N\big]}\hspace{0.15cm} \le \hspace{0.15cm} \frac{{\rm E}\big[H\big]}{{\rm E}\big[N\big]} \hspace{0.05cm}.\]

Hierbei ist vorausgesetzt, dass

• die (mittlere) Dauer eines Fehlerbündels in der Praxis sehr viel kleiner ist als der zu erwartende Abstand zweier Bündel,
• die (mittlere) Inter–Burst Time  $E\big[N\big]$  gleich dem Kehrwert der Burstfehlerwahrscheinlichkeit ist,
• der Erwartungswert im Zähler wie folgt abgeschätzt wird:

\[{\rm E}\big[H \big] \le \frac{1}{\rm Pr(Burstfehler)}\hspace{0.1cm} \cdot \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} \hspace{0.05cm}.\]

Bei der Herleitung dieser Schranke werden die paarweise Fehlerwahrscheinlichkeit  ${\rm Pr}\big [\varphi_0 → \varphi_i \big]$  sowie die Bhattacharyya–Abschätzung verwendet. Damit erhält man mit

• dem Pfadeingangsgewicht  $u(\varphi_i),$
• dem Pfadausgangsgewicht  $w(\varphi_i),$ und
• dem Bhattacharyya–Parameter  $\beta$

die folgende Abschätzung für die Bitfehlerwahrscheinlichkeit und bezeichnet diese als die  Viterbi–Schranke:

\[{\rm Pr(Bitfehler)}\le \sum_{\varphi_{\hspace{0.02cm}i} \in {\it \Phi}}\hspace{0.05cm} \hspace{0.05cm} u(\varphi_i) \cdot \beta^{w(\varphi_i)} \hspace{0.05cm}.\]

Dieses Zwischenergebnis lässt sich auch in anderer Form darstellen. Wir erinnern uns an die  erweiterte Pfadgewichtsfunktion

\[T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)} \hspace{0.05cm}.\]

Leitet man diese Funktion nach der Dummy–Eingangsvariablen  $U$  ab, so erhält man

\[\frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \cdot U^{{ u}(\varphi_j)-1} \hspace{0.05cm}.\]

Setzen wir schließlich noch für die Dummy–Eingangsvariable  $U = 1$, so erkennen wir den Zusammenhang zum obigen Ergebnis:

\[\left [ \frac {\rm d}{{\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{ U=1}} = \sum_{\varphi_j \in {\it \Phi}}\hspace{0.1cm} { u}(\varphi_j) \cdot X^{w(\varphi_j)} \hspace{0.05cm}.\]

$\text{Fazit:}$  Die  Bitfehlerwahrscheinlichkeit  eines Faltungscodes kann mit der erweiterten Pfadgewichtsfunktion in geschlossener Form abgeschätzt werden:

\[{\rm Pr(Bitfehler)} \le {\rm Pr(Viterbi)} = \left [ \frac {\rm d}{ {\rm d}U}\hspace{0.2cm}T_{\rm enh}(X, U) \right ]_{\substack{X=\beta \\ U=1} } \hspace{0.05cm}.\]

Man spricht von der  Viterbi–Schranke. Dabei leitet man die erweiterte Pfadgewichtsfunktion nach dem zweiten Parameter  $U$  ab und setzt anschließend 

• $X = \beta$, 
• $U = 1$.

Hinweis:   In  Aufgabe 3.14  werden die  Viterbi–Schranke  und die  Bhattacharyya–Schranke  für den Rate–$1/2$–Standardcode und das  BSC–Modell  numerisch ausgewertet.

AWGN–Bitfehlerwahrscheinlichkeit von Faltungscodes

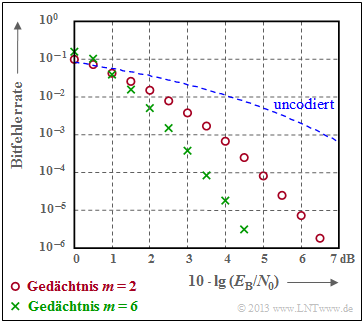
$\text{Beispiel 5:}$  Die Grafik verdeutlicht die gute Korrekturfähigkeit der Faltungscodes beim  AWGN–Kanal.

• Rote Kreise kennzeichnen die Bitfehlerrate für unseren Rate–$1/2$–Standardcode mit Memory  $m = 2$.
  
• Grüne Kreuze markieren einen Faltungscode mit  $m = 6$, dem so genannten  Industrie–Standardcode.
  
  

Insbesondere Codes mit großem Gedächtnis  $m$  führen zu großen Gewinnen gegenüber uncodierter Übertragung (gestrichelte Kurve).

Aufgaben zum Kapitel

Aufgabe 3.12: Pfadgewichtsfunktion

Aufgabe 3.12Z: Ring und Rückkopplung

Aufgabe 3.13: Nochmals zu den Pfadgewichtsfunktionen

Aufgabe 3.14: Fehlerwahrscheinlichkeitsschranken