Exercise 4.09: Recursive Systematic Convolutional Codes

• Return to book

State transition diagram
of an RSC code

In  $\text{Exercise 4.8}$  important properties of convolutional codes have already been derived from the state transition diagram,  assuming a non-recursive filter structure.

Now a rate  $1/2$  RSC code is treated in a similar manner.  Here  $\rm RSC$  stands for  "recursive systematic convolutional".

The transfer function matrix of an RSC convolutional code can be specified as follows:

$${\boldsymbol{\rm G}}(D) = \left [ 1\hspace{0.05cm},\hspace{0.3cm} G^{(2)}(D)/G^{(1)}(D) \right ] \hspace{0.05cm}.$$

Otherwise,  exactly the same conditions apply here as in Exercise 4.8.  We refer again to the following theory pages:

1. "Systematic convolutional codes"
2. "Representation in the state transition diagram"
3. "Definition of the free distance"
4. "GF(2) description forms of a digital filter"
5. "Application of the  $D$–transform to rate  $1/n$  convolution encoders"
6. "Filter structure with fractional–rational transfer function"

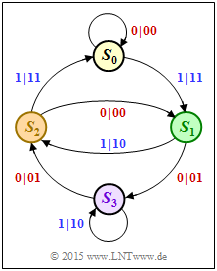
In the state transition diagram,  two arrows go from each state.  The label is  "$u_i \hspace{0.05cm}| \hspace{0.05cm} x_i^{(1)}x_i^{(2)}$".  For a systematic code,  this involves:

• The first code bit is identical to the information bit:   $\hspace{0.2cm} x_i^{(1)} = u_i ∈ \{0, \, 1\}$.
• The second code bit is the parity-check bit:   $\hspace{0.2cm} x_i^{(2)} = p_i ∈ \{0, \, 1\}$.

Hints:

• The exercise refers to the chapter  "Basics of Turbo Codes".

• The following vectorial quantities are used in the questions for this exercise:

• the information sequence:  $\hspace{0.2cm} \underline{u} = (u_1, \, u_2, \text{...} \hspace{0.05cm} )$,
• the parity-check sequence:  $\hspace{0.2cm} \underline{p} = (p_1, \, p_2, \text{...} \hspace{0.05cm})$,
• the impulse response:  $\hspace{0.2cm} \underline{g} = (g_1, \, g_2, \text{...} \hspace{0.05cm} ); \hspace{0.2cm}$ this is equal to the parity sequence  $\underline{p}$  for  $\underline{u} = (1, \, 0, \, 0, \text{...} \hspace{0.05cm} )$.

Questions

1

What is the impulse response  $\underline{g}$ ?

	$\underline{g} = (1, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, 1, \text{...} \hspace{0.05cm})$.
	$\underline{g} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \text{...} \hspace{0.05cm})$.

2

It holds   $\underline{u} = (1, \, 1, \, 0, \, 1)$.  Which statements hold for the parity sequence  $\underline{p}$ ?

	$\underline{p} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \text{...} \hspace{0.05cm})$.
	$\underline{p} = (1, \, 0, \, 0, \, 0, \, 0, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \text{...} \hspace{0.05cm})$.
	With limited information sequence  $\underline{u}$   ⇒   $\underline{p}$  is also limited.

3

What is the  $D$–transfer function  $G(D)$?

	$G(D) = 1 + D + D^2 + D^4 + D^5 + D^7 + D^8 + \text{...} \hspace{0.05cm}$.
	$G(D) = (1 + D^2)/(1 + D + D^2)$.
	$G(D) = (1 + D + D^2)/(1 + D^2)$.

4

Now let  $\underline{u} = (1, \, 1, \, 1)$.  Which statements hold for the parity sequence  $\underline{p}$?

	$\underline{p} = (1, \, 0, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \text{...} \hspace{0.05cm})$.
	$\underline{p} = (1, \, 0, \, 0, \, 0, \, 0, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \text{...} \hspace{0.05cm})$.
	With limited information sequence  $\underline{u}$   ⇒   $\underline{p}$  is also limited.

5

What is the free distance  $d_{\rm F}$  of this RSC encoder?

$d_{\rm F} \ = \ $

Solution

Solution

(1)  Tracing the transitions in the state diagram for the sequence  $\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0)$  at the input, we get the path

$$S_0 → S_1 → S_3 → S_2 → S_1 → S_3 → S_2 → S_1 → S_3 → \hspace{0.05cm}\text{...} \hspace{0.05cm}$$

• For each transition, the first code symbol $x_i^{(1)}$ is equal to the information bit $u_i$ and the code symbol $x_i^{(2)}$ indicates the parity-check bit $p_i$.
• This gives the result corresponding to solution proposition 1:

$$\underline{p}= (\hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm}1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 0\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm}, \hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\text{...} \hspace{0.05cm}) = \underline{g}\hspace{0.05cm}.$$

• For any RSC code, the impulse response $\underline{g}$ is infinite in length and becomes periodic at some point, in this example with period  $P = 3$  and  "$0, \, 1, \, 1$".

Clarification of  $\underline{p} = (1, \, 1, \, 0, \, 1)^{\rm T} \cdot \mathbf{G}$

(2)  The graph shows the solution of this exercise according to the equation  $\underline{p} = \underline{u}^{\rm T} \cdot \mathbf{G}$.

• Here the generator matrix  $\mathbf{G}$  is infinitely extended downward and to the right.
• The correct solution is proposal 2.

(3)  Correct are the proposed solutions 1 and 2:

• Between the impulse response $\underline{g}$ and the $D$–transfer function $\mathbf{G}(D)$ there is the relation according to the first proposed solution:

$$\underline{g}= (\hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}0\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}0\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, \hspace{-0.05cm}1\hspace{-0.05cm}, ... ) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad G(D) = 1\hspace{-0.05cm}+\hspace{-0.05cm} D\hspace{-0.05cm} +\hspace{-0.05cm} D^2\hspace{-0.05cm} +\hspace{-0.05cm} D^4 \hspace{-0.05cm}+\hspace{-0.05cm} D^5 \hspace{-0.05cm}+\hspace{-0.05cm} D^7 \hspace{-0.05cm}+\hspace{-0.05cm} D^8 + \hspace{0.05cm} \text{...} \hspace{0.05cm}.$$

• Let us now examine the second proposal:

$$G(D) = \frac{1+ D^2}{1+ D + D^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G(D) \cdot [1+ D + D^2] = 1+ D^2 \hspace{0.05cm}.$$

• The following calculation shows that this equation is indeed true:

$$(1+ D+ D^2+ D^4 +D^5 + D^7 + D^8 + \hspace{0.05cm} \text{...}) \cdot (1+ D+ D^2 ) =$$

$$=1+ D+ D^2\hspace{1.05cm} +D^4 + D^5 \hspace{1.05cm} +D^7 + D^8 \hspace{1.05cm} + D^{10}+ \hspace{0.05cm} \text{...}$$

$$+ \hspace{0.8cm}D+ D^2+D^3 \hspace{1.05cm}+ D^5 + D^6 \hspace{1.05cm} +D^8 + D^9 \hspace{1.25cm} +\hspace{0.05cm} \text{...}$$

$$+ \hspace{1.63cm} D^2+D^3+ D^4 \hspace{1.05cm}+ D^6 +D^7 \hspace{1.05cm}+ D^9 + D^{10} \hspace{0.12cm}+ \hspace{0.05cm} \text{...}$$

$$=\underline{1\hspace{0.72 cm}+ D^2} \hspace{0.05cm}.$$

• But since equation (2) is true, the last equation must be false.

(4)  Correct is only the proposed solution 1:

• From $\underline{u} = (1, \, 1, \, 1)$ follows $U(D) = 1 + D + D^2$. Thus also holds:

$$P(D) = U(D) \cdot G(D) = (1+D+D^2) \cdot \frac{1+D^2}{1+D+D^2}= 1+D^2\hspace{0.3cm} \Rightarrow\hspace{0.3cm} \underline{p}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm})\hspace{0.05cm}.$$

• If the variables  $u_i$  and  $g_i$  were real-valued, the (discrete) convolution  $\underline{p} = \underline{u} * \underline{g}$  would always lead to a broadening  ⇒   $\underline{p}$  in this case would be broader than  $\underline{u}$  and also broader than  $\underline{g}$.
• On the other hand, for  $u_i ∈ {\rm GF}(2)$  and  $g_i ∈ {\rm GF}(2)$  it may (but need not) happen that even with unbounded  $\underline{u}$  or for unbounded  $\underline{g}$  the convolution product  $\underline{p} = \underline{u} * \underline{g}$  is bounded.

Verdeutlichung von  $\underline{p} = (1, \, 1, \, 1, \, 0, \, ...)^{\rm T} \cdot \mathbf{G}$

• The result is finally checked according to the equation $\underline{p} = \underline{u}^{\rm T} \cdot \mathbf{G}$ is checked.

(5)  Following a similar procedure as in "Exercise A4.8, (4)", one can see:

• The free distance is again determined by the path  $S_0 → S_0 → S_1 → S_2 → S_0 → S_0 → \hspace{0.05cm}\text{...}\hspace{0.05cm}$.
• But the associated code sequence  $\underline{x}$  is now  " $00 \ 11 \ 10 \ 11 \ 00 \ ...$".
• This gives the free distance to  $d_{\rm F} \ \underline{= 5}$.
• In contrast, in the non-recursive code (exercise 4.8), the free distance was  $d_{\rm F} = 3$.