Exercise 4.5Z: About Spread Spectrum with UMTS

Source signal and spread signal

With UMTS/CDMA, the so-called "pseudo-noise" modulation is applied (Direct Sequence Spread Spectrum DS-SS):

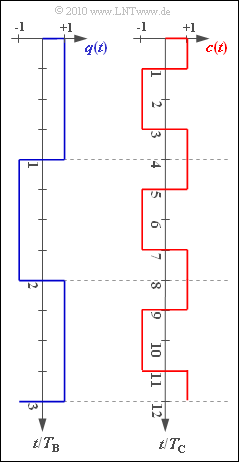
The rectangular digital signal $q(t)$ is thereby multiplied by the spreading signal $c(t)$ to give the transmitted signal $s(t)$.
This is higher in frequency by the spreading factor $J$ than $q(t)$, and is referred to as band spreading.
At the receiver, the same spreading signal $c(t)$ is added in phase synchronism, reversing the band spreading ⇒ band compression.

The graph shows example signal waveforms for $q(t)$ and $c(t)$.

In the subtask (5) is asked about transmit chips. For example, the "transmit chip" $s_{3}$ denotes the constant signal value of $s(t)$ in the time interval $2 T_{\rm C} ... 3 T_{\rm C}$.

Hints:

This exercise mostly refers to the page "Telecommunications Aspects of UMTS".
For calculation of chip duration $T_{\rm C}$ reference is made to the theory page "Physical channels" in the chapter "UMTS network architecture".
There you will find, among other things, the information that on the so-called Dedicated Physical Channel ('DPCH ) in ten milliseconds exactly $15 \cdot 2560$ chips are transmitted.

Questions

	With UMTS, the bit duration $T_{\rm B}$ is fixed.
	For UMTS, the chip duration $T_{\rm C}$ is fixed.
	Both quantities depend on the channel conditions.

$T_{\rm C} \hspace{0.28cm} = \ $

$ \ \rm µ s$

$R_{\rm C} \hspace{0.2cm} = \ $

$ \ \rm Mchip/s$

$J \ = \ $

$ R_{\rm B} \ = \ $

$ \ \rm kbit/s$

$s_{3} \ = \ $

$s_{4} \ = \ $

$s_{5} \ = \ $

$s_{6} \ = \ $

Solution

(1) Correct is the answer 2:

Fixed for UMTS is the chip duration $T_{\rm C}$, which is still to be calculated in the subtask (2).
The larger the spreading degree $J$ is, the larger the bit duration is.

(2) According to the note on the information page, exactly $15 \cdot 2560 = 38400$ chips are transferred in ten milliseconds.

Thus the chip rate $R_{\rm C} = 100 \cdot 38400 \ {\rm chips/s} \hspace{0.15cm}\underline{= 3.84 \ \rm Mchip/s}$.
The chip duration is the reciprocal of this: $T_{\rm C} \hspace{0.15cm}\underline{\approx 0.26 \ \rm µ s}$.

(3) Each data bit consists of four spreading chips ⇒ $\underline{J = 4}$.

(4) The bit rate is given by $J = 4$ to $R_{\rm B} \hspace{0.15cm}\underline{= 960 \ \rm kbit/s}$.

With the maximum spreading factor for UMTS $J = 512 $, on the other hand, the bit rate is only more $7.5 \ \rm kbit/s$.

(5) For the transmitted signal $s(t) = q(t) \cdot c(t)$.

The chips $s_{3}$ and $s_{4}$ of the transmitted signal belong to the first data bit $(q_{1} = +1)$:

$$s_3 = c_3 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_4 = c_4 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$

In contrast, the two other transmitting chips we are looking for are associated with the second data bit $(q_{2} = -1)$ :

$$s_5 = -c_5= -c_1 \hspace{0.15cm}\underline {= -1},\hspace{0.4cm}s_6 = -c_6= -c_2 \hspace{0.15cm}\underline {= +1}\hspace{0.05cm}.$$