Exercise 2.4Z: Repetition to IDFT

Five sample sets for $\rm IDFT$

In the Discrete Fourier Transform $\rm (DFT)$ from the time samples $d(\nu) \hspace{0.15cm} {\rm with} \hspace{0.15cm} \nu = 0$, ... , $N - 1$ the discrete spectral coefficients $D(\mu) \hspace{0.15cm} {\rm with} \hspace{0.15cm} \mu = 0$, ... , $N - 1$ calculated as follows:

$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

Here $w$ abbreviates the complex rotation factor, which is defined as follows:

$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$

Thus, for the Inverse Discrete Fourier Transform $\rm (IDFT)$ as an inverse function of $\rm DFT$:

$$ d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

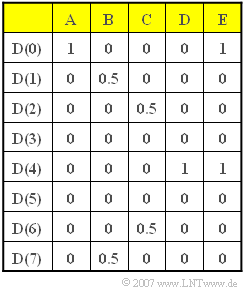
In this exercise, for different example sequences $D(\mu)$ - which in the above table are denoted by $\boldsymbol{\rm A}$, ... , $\boldsymbol{\rm E}$ - the time coefficients $d(\nu)$ are determined. Thus, it is always $N = 8$.

Hints:

This exercise refers to the theoretical foundations of the chapter "Discrete Fourier Transform" of the book "Signal Representation" and is identical to the one there "Exercise 5.2".

You can check your solution using the interactive applet "Discrete Fourier Transform" .

DFT and IDFT also play a major role in "DSM/DSL" .
In the corresponding chapter, spectral coefficients are denoted by $D_k$ and time samples are denoted by $s_l$. We apologize for this nomenclature discrepancy.
For the two running variables, with the DFT parameter $N = 8$: $0 \le k \le 7, \hspace{0.2cm}0 \le l \le 7 \hspace{0.05cm}.$

Questions

$d(0) \ = \ $

$d(1) \ = \ $

$d(0) \ = \ $

$d(1) \ = \ $

$d(0) \ = \ $

$d(1) \ = \ $

$d(0) \ = \ $

$d(1) \ = \ $

$d(0) \ = \ $

$d(1) \ = \ $

Solution

(1) From the IDFT equation, $D(\mu) = 0$ for $\mu \neq 0$ is obtained for the time coefficients with indices $0 ≤ \nu ≤ 7$:

$$d(\nu) = D(0) \cdot w^0 = D(0) \ = \ 1\hspace{0.3cm} \rightarrow\hspace{0.3cm}\underline{d(0) = d(1) \ = \ 1}.$$

This set of parameters thus describes the discrete form of the Fourier correspondence of the DC signal:

$$x(t) = 1 \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = {\delta}(f) \hspace{0.05cm}.$$

(2) Here all spectral coefficients are $0$ except $D_{1} = D_{7} = 0.5$. It follows that for $0 ≤ \nu ≤ 7$:

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (7\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} \hspace{0.05cm}.$$

However, due to periodicity, the following is also true:

$$d(\nu) \ = \ 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left({\pi}/{4} \cdot \nu \right)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{d(0) = 1, \hspace{0.2cm}d(1) = {1}/{\sqrt{2}} \approx 0.707 \hspace{0.05cm}}.$$

Thus, it is the discrete-time equivalent of

$$x(t) = \cos(2 \pi \cdot f_{\rm A} \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X(f) = {1}/{2} \cdot {\delta}(f + f_{\rm A}) + {1}/{2} \cdot {\delta}(f - f_{\rm A}) \hspace{0.05cm},$$

where $f_{\rm A}$ denotes the smallest frequency that can be represented in the DFT.

(3) Compared to the subtask (2), the frequency is now twice as large, namely $2 \cdot f_{\rm A}$ instead of $f_{\rm A}$:

$$x(t) = \cos(2 \pi \cdot (2f_{\rm A}) \cdot t) \hspace{0.2cm}\circ\!-\!-\!-\!-\!-\!-\!-\!-\bullet\, \hspace{0.2cm} X(f) = {1}/{2} \cdot {\delta}(f + 2f_{\rm A}) + {1}/{2}\cdot {\delta}(f - 2f_{\rm A}) \hspace{0.05cm},$$

Thus the sequence $〈d(\nu)〉$ describes two periods of the cosine oscillation, and it holds for $0 ≤ \nu ≤ 7$:

$$d(\nu) \ = \ 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left({\pi}/{2} \cdot \nu \right)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{d(0) = 1, \hspace{0.2cm}d(1) = 0 }\hspace{0.05cm}.$$

(4) By further doubling the cosine frequency to $4f_{\rm A}$, one finally arrives at the continuous-time Fourier correspondence

$$d(\nu) = 0.5 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} + 0.5 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \cos \left(\pi \cdot \nu \right) \hspace{0.05cm}$$

and thus to the time coefficients

$$d(0) = d(2) =d(4) =d(6)= +1, \hspace{0.2cm}d(1) =d(3) =d(5) =d(7) = -1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{d(0) = +1, \hspace{0.2cm}d(1) = -1 }\hspace{0.05cm}.$$

Note that the two Dirac functions coincide in the discrete-time representation due to periodicity.
That is, The coefficients $D(4) = 0.5$ and $D(-4) = 0.5$ add up to $D(4) = 1$.

(5) The Discrete Fourier Transform is also linear. Therefore, the superposition principle is still applicable.

The coefficients $D(\mu)$ from column $\boldsymbol{\rm E}$ are obtained as the sums of columns $\boldsymbol{\rm A}$ and $\boldsymbol{\rm D}$.
Therefore, the alternating sequence $〈d(\nu)〉$ according to subtask (4) becomes the sequence shifted up by 1:

$$d(0) =d(2) =d(4) =d(6)= 2, \hspace{0.2cm}d(1) =d(3) =d(5) =d(7) = 0\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{d(0) = 2, \hspace{0.2cm}d(1) =0 }\hspace{0.05cm}. $$